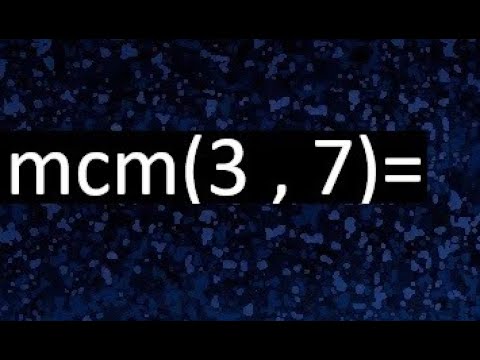¡Hola! Hoy vamos a hablar de un concepto matemático que puede parecer un poco intimidante al principio, pero no te preocupes, ¡lo desglosaremos juntos! El Mínimo Común Múltiplo, o MCM, es un término que aparece a menudo en la aritmética y es fundamental en la resolución de problemas que involucran fracciones, múltiplos y divisores. En este artículo, nos centraremos en encontrar el Mínimo Común Múltiplo de dos números específicos: 3 y 7. ¿Listo para sumergirte en el fascinante mundo de los números? ¡Vamos allá!
¿Qué es el Mínimo Común Múltiplo?
Antes de lanzarnos a calcular el MCM de 3 y 7, es crucial entender qué es realmente este concepto. Imagina que el Mínimo Común Múltiplo es como un punto de encuentro para los múltiplos de dos números. En otras palabras, es el menor número que es múltiplo de ambos. Por ejemplo, si pensamos en los múltiplos de 3, tenemos 3, 6, 9, 12, 15, y así sucesivamente. Para 7, los múltiplos son 7, 14, 21, 28, y así sigue. El MCM es simplemente el primer número que aparece en ambas listas de múltiplos. Pero, ¿cómo encontramos ese número? ¡Vamos a descubrirlo!
Métodos para Calcular el Mínimo Común Múltiplo
Listar los Múltiplos
Una forma sencilla de encontrar el MCM es listar los múltiplos de cada número hasta que encontremos el primero que coincida. Como mencionamos antes, los múltiplos de 3 son 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60… y los múltiplos de 7 son 7, 14, 21, 28, 35, 42, 49, 56, 63, 70… Si observamos ambas listas, el primer número que aparece en ambas es 21. Por lo tanto, el Mínimo Común Múltiplo de 3 y 7 es 21. ¡Fácil, verdad?
Método de la Descomposición en Factores Primos
Si eres un poco más aventurero y quieres profundizar, podemos utilizar el método de la descomposición en factores primos. Este método puede parecer un poco más complicado, pero es bastante efectivo. Primero, descomponemos cada número en sus factores primos. Para 3, el único factor primo es 3. Para 7, igualmente, el único factor primo es 7. Ahora, tomamos cada factor primo, elevamos a la mayor potencia que aparece en cualquiera de las descomposiciones y multiplicamos. En este caso, sería 31 * 71 = 21. ¡Y ahí lo tienes!
Aplicaciones del Mínimo Común Múltiplo
Ahora que sabemos cómo encontrar el MCM, es interesante pensar en por qué es útil. ¿Te has preguntado alguna vez por qué necesitas encontrar el MCM en la vida real? Imagina que estás cocinando y tienes dos recetas que requieren diferentes tiempos de cocción. Si una receta requiere 3 minutos y la otra 7 minutos, el MCM te dirá cuándo ambas estarán listas al mismo tiempo. Esto puede ayudarte a planificar mejor y evitar que la comida se queme. ¡La matemática puede ser muy práctica!
Ejemplos Prácticos
Ejemplo 1: Fracciones
Imagina que tienes dos fracciones: 1/3 y 1/7. Si quisieras sumarlas, necesitarías un denominador común. Aquí es donde entra el MCM. El MCM de 3 y 7 es 21, así que puedes convertir ambas fracciones a 21 como denominador: 1/3 se convierte en 7/21 y 1/7 se convierte en 3/21. Ahora puedes sumarlas fácilmente: 7/21 + 3/21 = 10/21.
Ejemplo 2: Planificación de Eventos
Supongamos que organizas eventos cada 3 días y cada 7 días. Quieres saber cuándo ocurrirán en el mismo día. Al calcular el MCM de 3 y 7, que es 21, sabes que ambos eventos coincidirán cada 21 días. Esto te ayuda a planificar tus actividades de manera más eficiente.
Consejos para Recordar el Mínimo Común Múltiplo
Ahora que has aprendido sobre el MCM, aquí hay algunos consejos para recordarlo. Primero, siempre recuerda que el MCM es el menor múltiplo común. Puedes practicar listando múltiplos de diferentes números hasta que te sientas cómodo. También, al descomponer números en factores primos, trata de visualizarlo como un juego. ¡Cuantos más factores encuentres, más puntos ganarás!
¿El MCM siempre es mayor que los números originales?
No necesariamente. El MCM de dos números puede ser uno de los números originales si uno es un múltiplo del otro. Por ejemplo, el MCM de 4 y 8 es 8.
¿Puedo calcular el MCM de más de dos números?
¡Por supuesto! Para calcular el MCM de más de dos números, simplemente encuentra el MCM de los primeros dos, y luego usa ese resultado para calcular el MCM con el siguiente número, y así sucesivamente.
¿Qué pasa si los números son primos entre sí?
Si los números son primos entre sí, como 3 y 7, su MCM será simplemente el producto de ambos. En este caso, 3 * 7 = 21, que es lo que encontramos antes.
¿El MCM se utiliza en otras áreas de la matemática?
Sí, el MCM es muy útil en álgebra, teoría de números y en la resolución de problemas de programación. También se utiliza en situaciones cotidianas como la planificación de horarios y la gestión de recursos.
En conclusión, encontrar el Mínimo Común Múltiplo de 3 y 7 es un proceso sencillo y muy útil en diversas situaciones. Ya sea que estés cocinando, organizando eventos o resolviendo fracciones, el MCM puede facilitarte la vida. Así que la próxima vez que te enfrentes a un problema matemático, recuerda que el MCM es tu aliado. ¡Espero que hayas disfrutado este viaje a través del mundo de los números!