¡Hola, amante de las matemáticas! Si alguna vez te has preguntado cómo encontrar los puntos de corte de una función, has llegado al lugar correcto. Los puntos de corte son esos lugares especiales donde una función se encuentra con el eje X o el eje Y. ¿Te suena? En esta guía, te llevaré de la mano a través de un proceso sencillo y directo para que puedas dominar este concepto y aplicar lo aprendido en tus estudios. Así que, ¡prepárate para sumergirte en el fascinante mundo de las funciones!
¿Qué son los Puntos de Corte?
Antes de sumergirnos en el proceso, aclaremos qué son exactamente estos puntos de corte. Imagina que estás en un parque, y te encuentras con dos caminos que se cruzan. Ese cruce es un punto de corte. En términos matemáticos, los puntos de corte son las coordenadas donde una función intersecta los ejes de coordenadas. Hay dos tipos principales: el punto de corte con el eje Y y los puntos de corte con el eje X.
Punto de Corte con el Eje Y
El punto de corte con el eje Y es el lugar donde la función toca el eje vertical. Para encontrar este punto, simplemente necesitas evaluar la función en x = 0. Así de fácil. Por ejemplo, si tienes la función f(x) = 2x + 3, para encontrar el punto de corte con el eje Y, sustituimos x por 0:
f(0) = 2(0) + 3 = 3
Así que el punto de corte con el eje Y es (0, 3). ¡Ya tenemos nuestro primer punto!
Puntos de Corte con el Eje X
Ahora, hablemos de los puntos de corte con el eje X. Estos son un poco más interesantes porque implican resolver una ecuación. Para hallarlos, necesitas encontrar los valores de x que hacen que la función sea igual a cero. En otras palabras, buscas las soluciones de la ecuación f(x) = 0. Siguiendo con el ejemplo anterior, tenemos:
2x + 3 = 0
Resolviendo esta ecuación, restamos 3 de ambos lados:
2x = -3
Y luego dividimos entre 2:
x = -3/2
Así que el punto de corte con el eje X es (-3/2, 0). ¡Genial, ya tenemos los dos puntos de corte!
Un Ejemplo Completo
Ahora que hemos cubierto lo básico, hagamos un ejemplo más completo. Supongamos que tenemos la función cuadrática f(x) = x² – 4x + 3. Queremos encontrar tanto el punto de corte con el eje Y como los puntos de corte con el eje X.
Punto de Corte con el Eje Y
Para encontrar el punto de corte con el eje Y, evaluamos la función en x = 0:
f(0) = (0)² – 4(0) + 3 = 3
Entonces, el punto de corte con el eje Y es (0, 3).
Puntos de Corte con el Eje X
Ahora, para encontrar los puntos de corte con el eje X, debemos resolver la ecuación:
x² – 4x + 3 = 0
Este es un trinomio que podemos factorizar:
(x – 1)(x – 3) = 0
De aquí, encontramos que x = 1 y x = 3. Por lo tanto, los puntos de corte con el eje X son (1, 0) y (3, 0).
¿Qué Hacer si la Función es Más Compleja?
Puede que te encuentres con funciones más complejas que no se pueden factorizar fácilmente. En esos casos, es posible que necesites usar la fórmula cuadrática. La fórmula cuadrática es:
x = (-b ± √(b² – 4ac)) / 2a
Así que si tienes una función como f(x) = 2x² + 4x + 2, puedes identificar a, b y c como 2, 4 y 2, respectivamente, y aplicar la fórmula. Recuerda que el discriminante (b² – 4ac) te dirá cuántas soluciones tiene la ecuación:
- Si es mayor que 0, hay dos soluciones reales.
- Si es igual a 0, hay una solución real (la parábola toca el eje X).
- Si es menor que 0, no hay soluciones reales (la parábola no cruza el eje X).
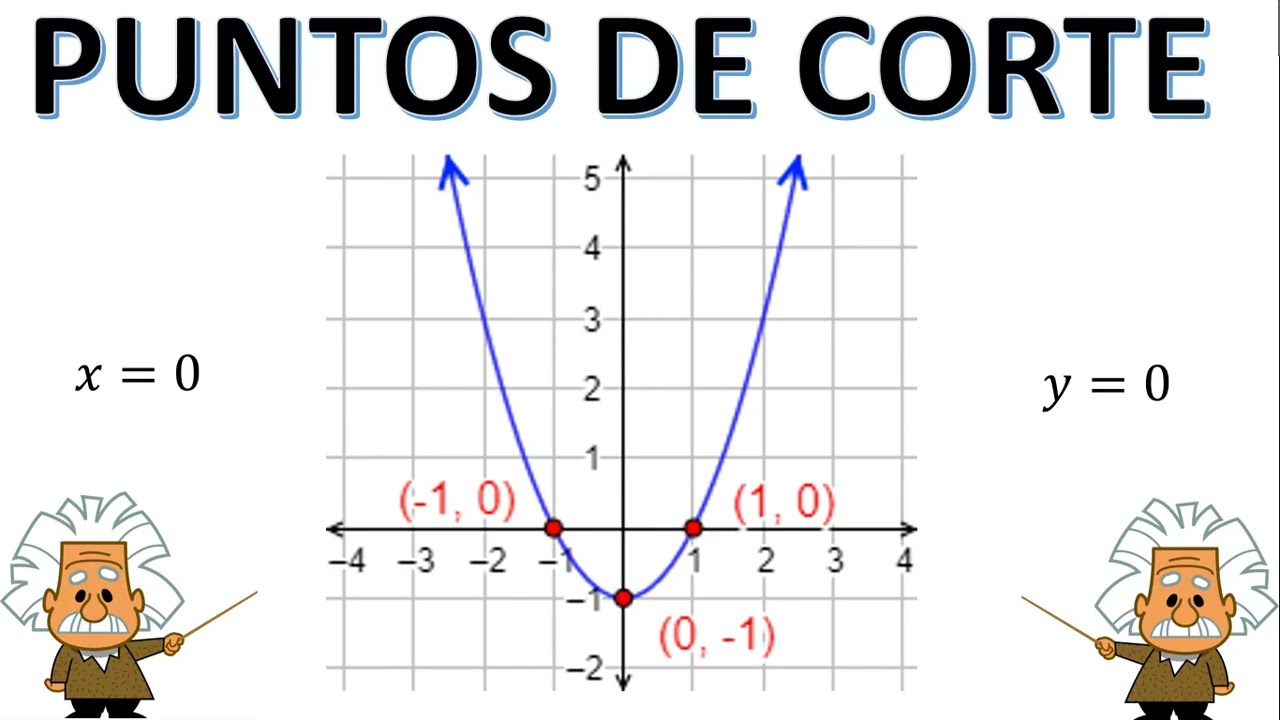
Visualizando los Puntos de Corte
Ahora que sabes cómo calcular los puntos de corte, es hora de visualizar lo que hemos encontrado. Dibujar la gráfica de la función puede ser increíblemente útil para entender cómo se comporta. Puedes usar herramientas en línea o software de gráficos, o incluso hacerlo a mano. Al graficar, marca los puntos de corte que has encontrado. ¡Es como marcar hitos en un mapa!
Errores Comunes al Hallar Puntos de Corte
Aunque ya estás bien encaminado, es importante estar consciente de algunos errores comunes que podrías cometer al calcular puntos de corte:
- Olvidar evaluar en x = 0 para el eje Y: A veces, la gente se salta este paso. Recuerda, es crucial.
- Confundir los signos: En la ecuación, asegúrate de prestar atención a los signos, ya que pueden cambiar la solución.
- No comprobar tus respuestas: Siempre es buena idea sustituir tus soluciones en la función original para verificar que son correctas.
Práctica hace al Maestro
Como en cualquier habilidad, la práctica es clave. Intenta resolver diferentes tipos de funciones. Comienza con funciones lineales y luego avanza a funciones cuadráticas, cúbicas y más complejas. Cuanto más practiques, más cómodo te sentirás. Recuerda, cada error es una oportunidad para aprender algo nuevo.
Así que ahí lo tienes, una guía completa para hallar los puntos de corte de una función. Desde entender qué son hasta cómo encontrarlos, ahora estás equipado para enfrentarte a cualquier desafío que se te presente en el camino. Recuerda que las matemáticas son como un rompecabezas: cada pieza tiene su lugar, y al final, todo cobra sentido.
¿Puedo hallar puntos de corte con funciones que no son polinómicas?
Sí, puedes hallar puntos de corte con funciones no polinómicas, pero el método puede variar. Para funciones trigonométricas, exponenciales o logarítmicas, deberás aplicar sus respectivas propiedades.
¿Qué pasa si la función no corta el eje X?
Si el discriminante de la ecuación es menor que cero, significa que la función no tiene puntos de corte con el eje X, es decir, no toca el eje en ese rango de valores.
¿Es necesario graficar la función para encontrar los puntos de corte?
No es estrictamente necesario, pero graficar puede ayudarte a visualizar y entender mejor el comportamiento de la función. A veces, ver la gráfica puede hacer que todo cobre sentido.
¿Los puntos de corte siempre son números enteros?
No, los puntos de corte pueden ser fracciones, decimales o incluso números irracionales. Dependerá de la función específica que estés evaluando.
¿Cómo puedo practicar más para mejorar mis habilidades en este tema?
Busca ejercicios en libros de texto, plataformas en línea o incluso aplicaciones de matemáticas. También puedes trabajar con compañeros de estudio para resolver problemas juntos y aprender de los errores de los demás.