¿Alguna vez te has preguntado cómo determinar los puntos más altos y más bajos de una función? Estos puntos son conocidos como extremos relativos, y son fundamentales en el análisis de funciones. Al entender cómo calcularlos, no solo podrás resolver problemas matemáticos más fácilmente, sino que también podrás aplicar este conocimiento en situaciones del mundo real, como la optimización de recursos o el análisis de datos. Así que, ¡vamos a sumergirnos en este emocionante viaje hacia el corazón de las funciones!
¿Qué Son los Extremos Relativos?
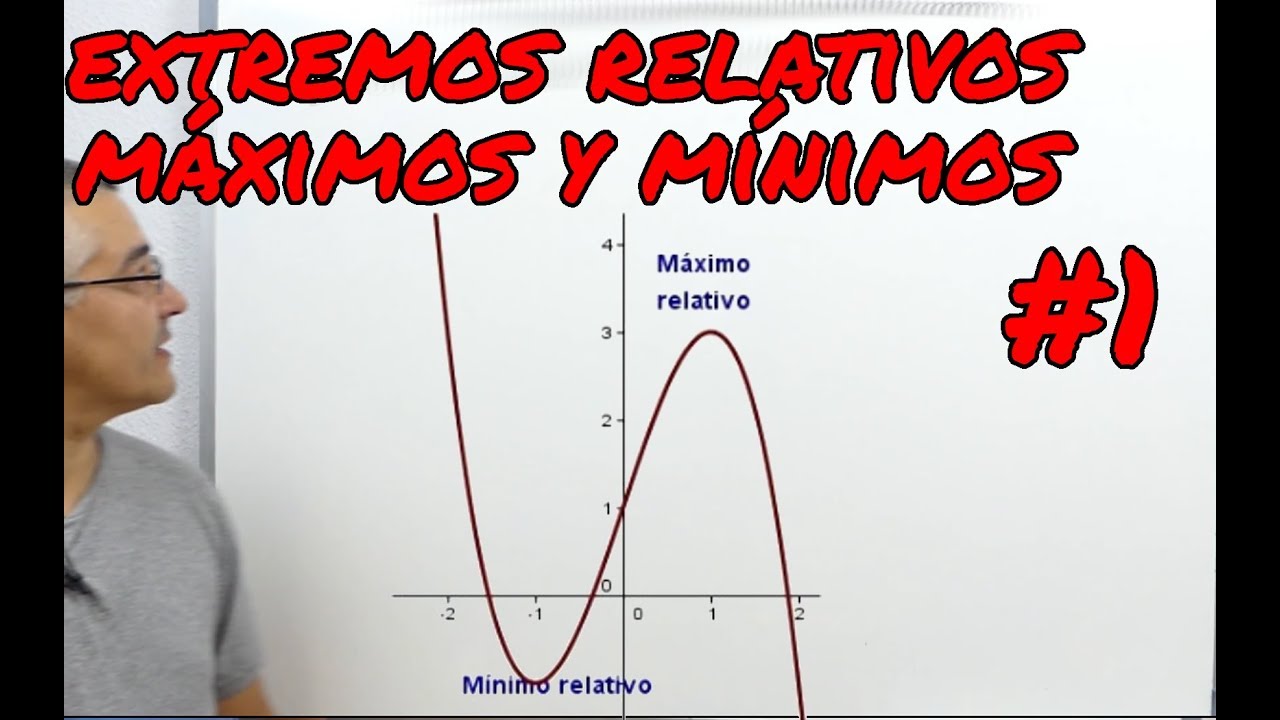
Los extremos relativos de una función son los puntos donde la función alcanza un valor máximo o mínimo en un intervalo específico. Imagina que estás en una montaña. El pico más alto que puedes ver desde tu posición es un extremo relativo máximo, mientras que el valle más profundo sería un extremo relativo mínimo. Estos puntos son cruciales en el estudio de funciones porque nos ayudan a entender su comportamiento y tendencia.
Pasos para Calcular los Extremos Relativos
Encuentra la Derivada de la Función
El primer paso para encontrar los extremos relativos es calcular la derivada de la función. La derivada nos dice cómo cambia la función en cada punto, lo que es esencial para identificar los máximos y mínimos. Si tienes una función f(x), la derivada se denota como f'(x). Si no estás familiarizado con el concepto de derivadas, piénsalo como una pendiente: si la pendiente es positiva, la función está subiendo; si es negativa, está bajando.
Igualar la Derivada a Cero
Una vez que tienes la derivada, el siguiente paso es igualarla a cero. Esto es crucial porque los extremos relativos ocurren donde la pendiente de la función es cero (es decir, donde la función deja de subir o bajar). Resolvemos la ecuación f'(x) = 0 para encontrar los valores de x que podrían ser extremos relativos. Estos puntos son como los momentos de pausa en una carrera: el corredor puede estar en su mejor momento, pero también podría estar a punto de caer.
Determina los Valores de la Función
Ahora que tienes los valores de x donde la derivada es cero, es hora de sustituir estos valores en la función original f(x). Esto te dará los valores correspondientes de y en esos puntos. Así podrás identificar los candidatos a extremos relativos. Imagina que estás tomando fotos de la montaña: cada vez que llegas a un nuevo pico, quieres capturar la vista, y aquí es donde registras esos puntos importantes.
Utiliza la Prueba de la Segunda Derivada
Para determinar si esos puntos son realmente máximos o mínimos, utilizamos la prueba de la segunda derivada. Calcula la segunda derivada de la función, f»(x). Si f»(x) > 0, el punto es un mínimo relativo; si f»(x) < 0, es un máximo relativo. Si f»(x) = 0, la prueba es inconclusa, y tendrás que buscar otras formas de determinar la naturaleza del punto. Es como un juez en un partido: tiene que decidir si la jugada fue buena o mala, pero a veces la decisión no es tan clara.
Analiza el Comportamiento en los Límites
No olvides analizar el comportamiento de la función en los extremos del intervalo en el que estás trabajando. A veces, los extremos relativos pueden no ser los puntos más altos o bajos si consideras todo el rango de la función. Es como mirar un paisaje: a veces, lo más impresionante está fuera de la vista inmediata. Asegúrate de considerar el contexto completo para tener una imagen clara.
Ejemplo Práctico
Supongamos que tenemos la función f(x) = -2x^2 + 4x + 1. Vamos a seguir los pasos que hemos mencionado.
Paso 1: Encuentra la Derivada
La derivada de nuestra función es f'(x) = -4x + 4.
Paso 2: Igualar la Derivada a Cero
Igualamos a cero: -4x + 4 = 0. Resolviendo, encontramos x = 1.
Paso 3: Determina los Valores de la Función
Ahora sustituimos x = 1 en la función original: f(1) = -2(1)^2 + 4(1) + 1 = 3. Entonces, tenemos el punto (1, 3).
Paso 4: Prueba de la Segunda Derivada
Calculamos la segunda derivada: f»(x) = -4. Dado que f»(x) < 0, el punto (1, 3) es un máximo relativo.
Paso 5: Analiza el Comportamiento en los Límites
En este caso, dado que es una parábola que se abre hacia abajo, podemos concluir que (1, 3) es el máximo en toda la función.
Consejos Adicionales
Recuerda que calcular extremos relativos puede ser un poco complicado al principio, pero con práctica se vuelve más sencillo. Aquí hay algunos consejos adicionales:
- Practica con Diferentes Funciones: Cuanto más practiques, mejor entenderás cómo funcionan las derivadas y los extremos.
- Visualiza la Función: A veces, graficar la función puede ayudarte a ver los extremos de una manera más clara.
- Consulta Recursos: No dudes en usar libros, videos o tutoriales en línea si te sientes atascado.
¿Qué pasa si la derivada nunca es cero?
Si la derivada nunca es cero, eso significa que la función no tiene extremos relativos en ese intervalo. Puede ser que la función esté siempre aumentando o siempre disminuyendo.
¿Cómo afecta la forma de la función a los extremos?
La forma de la función determina la cantidad y tipo de extremos. Por ejemplo, una parábola puede tener un máximo o un mínimo, mientras que funciones más complejas pueden tener múltiples extremos.
¿Se pueden encontrar extremos relativos en funciones no derivables?
En funciones no derivables, como las que tienen puntos angulosos o discontinuidades, se deben utilizar otros métodos, como la búsqueda de límites o la comparación de valores en intervalos.
¿Es necesario usar la segunda derivada para encontrar extremos?
No es estrictamente necesario, pero es muy útil. También puedes usar la prueba de la primera derivada, analizando el cambio de signo de f'(x) alrededor de los puntos críticos.
En resumen, calcular los extremos relativos de una función puede parecer intimidante, pero siguiendo estos pasos y practicando un poco, ¡te convertirás en un experto en poco tiempo! Así que, ¿estás listo para poner en práctica lo que has aprendido?