¡Hola, amigo lector! Hoy nos adentramos en un tema que puede parecer un poco intimidante al principio, pero que es fundamental en el mundo de las matemáticas y la programación: las funciones. Imagina que una función es como una máquina mágica: tú le das un input (entrada) y, tras un proceso, ella te devuelve un output (salida). ¿No es genial? En este artículo, desglosaremos las características más importantes de las funciones, cómo funcionan y por qué son tan útiles en nuestra vida diaria. Así que, ¡abróchate el cinturón y comencemos este viaje!
¿Qué es una Función?
Primero, aclaremos qué es una función. En términos simples, una función es una relación entre dos conjuntos de datos, donde a cada elemento del primer conjunto (llamado dominio) le corresponde exactamente un elemento del segundo conjunto (llamado codominio). Para ilustrarlo mejor, piensa en una máquina expendedora: tú eliges un número, metes una moneda y, si todo va bien, la máquina te entrega un refresco. Cada número que ingresas (tu input) tiene un resultado específico (tu output).
Características Clave de las Funciones
Ahora que tenemos una idea básica, hablemos de las características clave que hacen que las funciones sean tan especiales. Estas características son fundamentales para entender cómo funcionan y por qué son tan importantes en matemáticas y programación.
Unicidad
Una de las características más importantes de una función es la unicidad. Esto significa que cada input tiene un único output. Si piensas en nuestra máquina expendedora, si eliges el número 5, siempre obtendrás la misma bebida. No importa cuántas veces lo hagas, el resultado será el mismo. Esto es crucial porque garantiza que la función sea predecible y confiable. ¿Te imaginas si cada vez que presionaras un botón obtuvieras algo diferente? ¡Sería un caos!
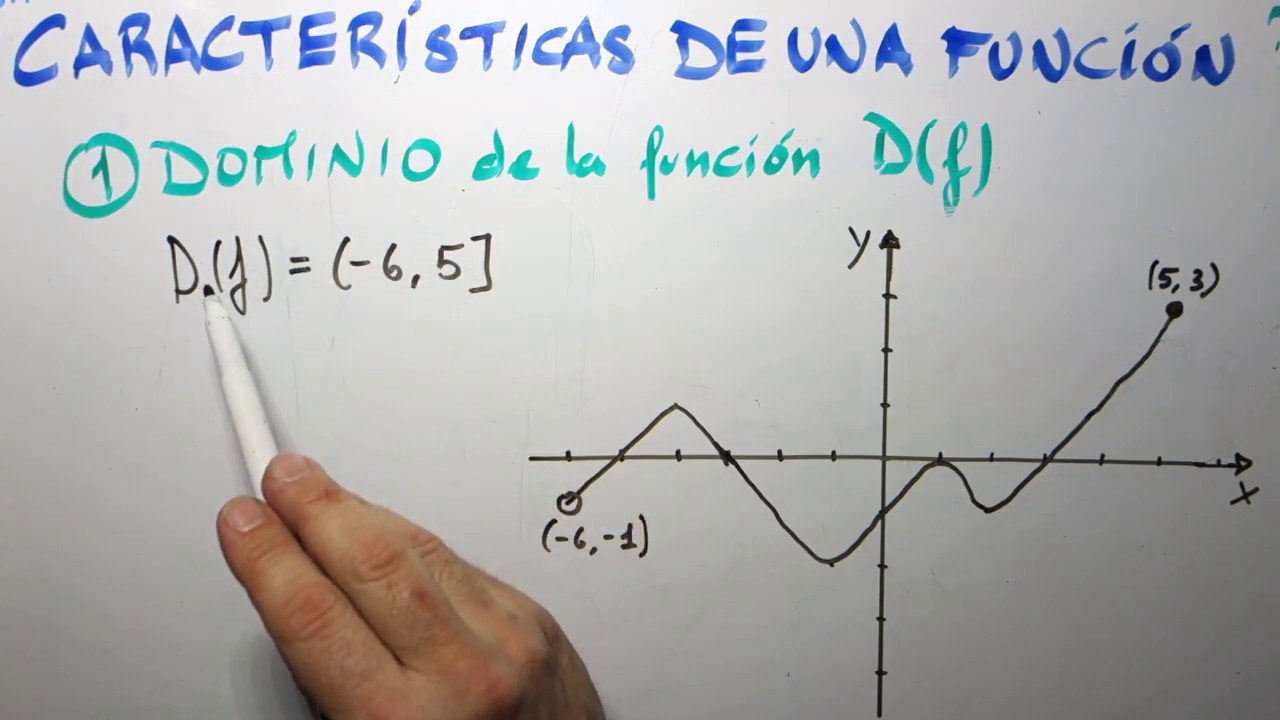
Dominio y Codominio
Hablemos ahora del dominio y el codominio. El dominio es el conjunto de todos los posibles inputs que puedes ingresar en la función. Por otro lado, el codominio es el conjunto de todos los posibles outputs que puedes obtener. Volviendo a nuestra máquina expendedora, el dominio serían los números de los botones disponibles y el codominio serían las bebidas que puedes recibir. Es fundamental entender estos conceptos para poder trabajar con funciones de manera efectiva.
Notación de Funciones
La notación es otra característica esencial. Normalmente, las funciones se denotan con letras como f(x) o g(x), donde ‘f’ o ‘g’ representan la función y ‘x’ es el input. Por ejemplo, si tienes una función que suma 2 a cualquier número que le des, podrías escribirla como f(x) = x + 2. Así, si le das 3, el output será 5. Es una forma compacta y clara de expresar lo que hace la función.
Tipos de Funciones
Las funciones pueden clasificarse en diferentes tipos según sus características. Algunas de las más comunes son:
1 Funciones Lineales
Las funciones lineales son aquellas que representan una línea recta en un gráfico. Tienen la forma f(x) = mx + b, donde ‘m’ es la pendiente y ‘b’ es el punto de intersección con el eje y. Estas funciones son fáciles de entender y graficar, y tienen aplicaciones en muchas áreas, desde la economía hasta la física.
2 Funciones Cuadráticas
Las funciones cuadráticas, en cambio, tienen la forma f(x) = ax² + bx + c. Aquí, el gráfico se asemeja a una parábola. Este tipo de función es muy común en problemas de optimización y también aparece en la trayectoria de objetos en movimiento. Si alguna vez has lanzado una pelota, has visto cómo describe una parábola en el aire.
3 Funciones Exponenciales
Las funciones exponenciales son aquellas que crecen o decrecen a un ritmo cada vez más rápido. Tienen la forma f(x) = a * b^x, donde ‘a’ es un número positivo y ‘b’ es la base. Estas funciones son fundamentales en el estudio de fenómenos como el crecimiento poblacional o la desintegración radiactiva. ¡Son realmente fascinantes!
Composición de Funciones
Una de las características más interesantes de las funciones es que puedes combinarlas. La composición de funciones es cuando tomas el output de una función y lo usas como input para otra. Por ejemplo, si tienes f(x) = x + 1 y g(x) = 2x, la composición se denotaría como (g ∘ f)(x). Esto significa que primero aplicas f, y luego aplicas g al resultado de f. Es como hacer un batido: primero eliges tus ingredientes (f) y luego los mezclas (g). ¡Delicioso y matemático!
Inversas de Funciones
Las funciones inversas son como el reverso de una moneda. Si tienes una función f(x), su inversa se denota como f⁻¹(x). Esta función toma el output de f y lo convierte de nuevo en el input original. Es como deshacer un nudo: si ataste un cordón, la función inversa sería el proceso de desatarlo. No todas las funciones tienen una inversa, pero cuando la tienen, son una herramienta muy poderosa.
Gráficas de Funciones
Una imagen vale más que mil palabras, y esto es especialmente cierto en matemáticas. Las gráficas de funciones nos permiten visualizar cómo se comporta una función. Por ejemplo, puedes ver cómo una función lineal se extiende en línea recta, mientras que una función cuadrática forma una hermosa parábola. Las gráficas nos ayudan a entender rápidamente las propiedades de una función, como su tendencia, intersecciones y máximos o mínimos.
Aplicaciones de las Funciones en la Vida Real
Ahora que hemos cubierto las características y tipos de funciones, es hora de hablar de cómo se aplican en el mundo real. Las funciones no son solo un concepto abstracto; están presentes en casi todos los aspectos de nuestra vida diaria. Desde la economía hasta la biología, las funciones nos ayudan a modelar y entender fenómenos complejos.
1 Economía y Finanzas
En economía, las funciones se utilizan para modelar la oferta y la demanda. Por ejemplo, la relación entre el precio de un producto y la cantidad que los consumidores están dispuestos a comprar se puede representar mediante una función. Esto ayuda a las empresas a tomar decisiones informadas sobre precios y producción.
2 Ciencias Naturales
En las ciencias naturales, las funciones son esenciales para describir fenómenos como el crecimiento de poblaciones o la velocidad de reacción de sustancias químicas. Las funciones exponenciales, por ejemplo, son fundamentales para entender el crecimiento poblacional, donde la población puede crecer de manera acelerada en condiciones favorables.
3 Tecnología y Programación
En programación, las funciones son la base de la mayoría de los lenguajes. Permiten a los programadores escribir código modular y reutilizable. Cada función puede encargarse de una tarea específica, lo que hace que el código sea más fácil de leer y mantener. Imagina que estás construyendo un coche: cada función es como una parte del motor que trabaja en conjunto para que el coche funcione correctamente.
En resumen, las funciones son un concepto fundamental que abarca muchas áreas del conocimiento. Desde su unicidad hasta su aplicación en la vida real, entender las funciones te brinda herramientas poderosas para resolver problemas y modelar situaciones. Ya sea que estés estudiando matemáticas, programando o simplemente tratando de entender el mundo que te rodea, las funciones son tus aliadas. Así que, la próxima vez que escuches la palabra «función», recuerda que detrás de ese término hay un mundo de posibilidades.
¿Qué es la diferencia entre una función y una relación?
Una relación puede tener múltiples outputs para un mismo input, mientras que una función siempre tiene un único output para cada input. Piensa en una función como un tipo de relación más restringida y predecible.
¿Cómo puedo saber si una función es invertible?
Una función es invertible si es uno a uno, es decir, si cada output corresponde a un único input. Para comprobar esto, puedes utilizar la prueba de la línea horizontal en el gráfico de la función.
¿Por qué son importantes las funciones en programación?
Las funciones en programación permiten la modularidad, lo que significa que puedes dividir tu código en partes más pequeñas y manejables. Esto hace que el código sea más fácil de entender y mantener.
¿Puedo tener funciones que no son matemáticas?
¡Claro! El concepto de función se puede aplicar en muchos contextos, no solo en matemáticas. Por ejemplo, en la vida cotidiana, puedes pensar en funciones como roles o tareas específicas que desempeñan las personas.
¿Qué herramientas puedo usar para graficar funciones?
Existen muchas herramientas en línea, como Desmos o GeoGebra, que te permiten graficar funciones fácilmente. También puedes usar software como Excel o incluso lenguajes de programación como Python para crear gráficos de funciones.