¿Qué es la Pendiente y por qué es Importante?
La pendiente de una recta es una de esas cosas que, aunque a veces parece complicada, realmente tiene un sentido muy práctico. Imagina que estás en una montaña y quieres saber qué tan empinada es la subida. Eso es precisamente lo que hace la pendiente: mide la inclinación de una línea. En matemáticas, la pendiente se utiliza para describir la relación entre dos variables. En este artículo, te guiaré a través de un proceso sencillo para calcularla, desglosando cada parte para que no te pierdas. Así que, ¡abrocha tu cinturón y vamos a aprender!
¿Qué es la Pendiente?
Primero, hablemos un poco más sobre qué es exactamente la pendiente. Matemáticamente, la pendiente se representa como «m» y se define como el cambio en la variable y (vertical) dividido por el cambio en la variable x (horizontal). Así que, si piensas en un gráfico de coordenadas, la pendiente te dice cuán rápido sube o baja la línea. Si te resulta más fácil, puedes imaginarlo como la inclinación de una rampa: cuanto más empinada es, mayor es la pendiente.
Fórmula de la Pendiente
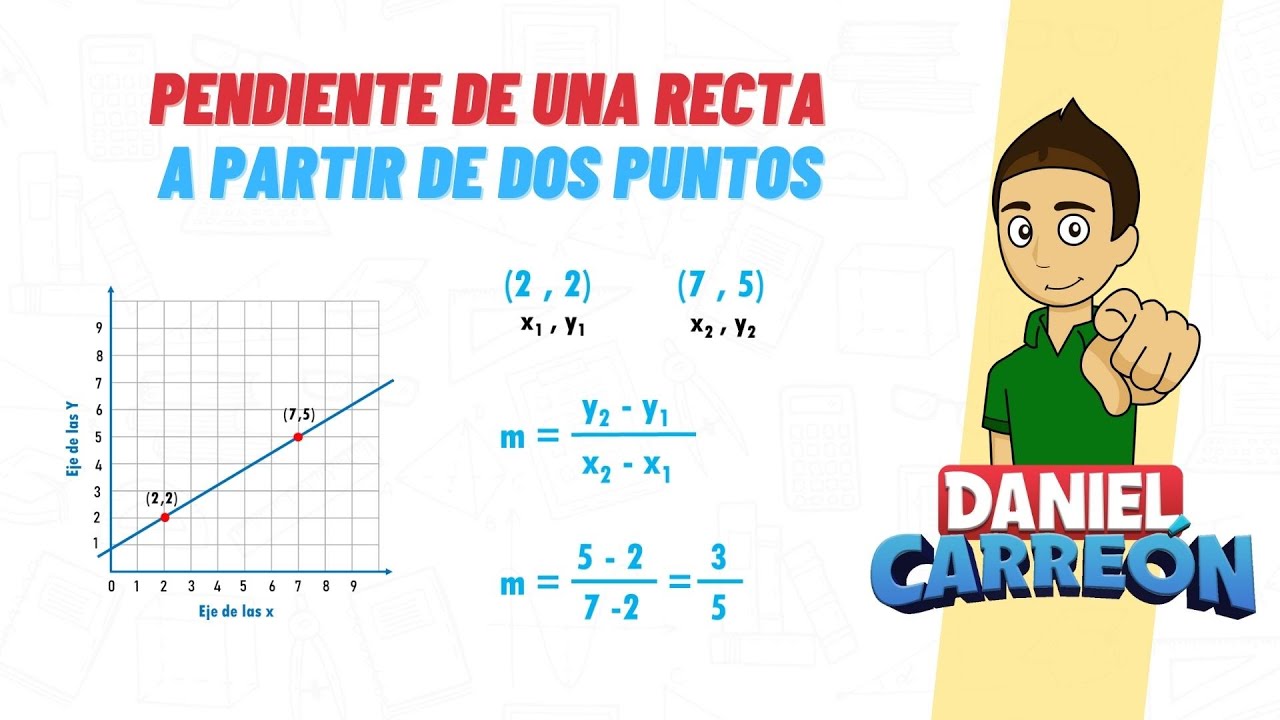
La fórmula básica para calcular la pendiente entre dos puntos (x₁, y₁) y (x₂, y₂) es:
m = (y₂ – y₁) / (x₂ – x₁).
No te preocupes si parece confuso, lo desglosaremos paso a paso. Lo importante aquí es que esta fórmula te ayudará a entender cómo se relacionan los dos puntos en el plano cartesiano.
Paso 1: Identificar los Puntos
Para calcular la pendiente, primero necesitas identificar dos puntos en la recta. Digamos que tienes los puntos A (2, 3) y B (5, 11). Aquí, el primer número es la coordenada x y el segundo es la coordenada y. Entonces, A tiene x₁ = 2 y y₁ = 3, y B tiene x₂ = 5 y y₂ = 11. Ahora que tenemos nuestros puntos, estamos listos para seguir adelante.
Paso 2: Sustitución en la Fórmula
Ahora, tomemos nuestra fórmula de la pendiente y sustituyamos los valores que tenemos. Recuerda que la fórmula es:
m = (y₂ – y₁) / (x₂ – x₁).
Sustituyendo los valores:
m = (11 – 3) / (5 – 2).
¿Ves cómo estamos usando los valores de nuestros puntos? Esto es crucial para obtener la respuesta correcta.
Realizando la Resta
Ahora, simplifiquemos eso. Primero, resta las coordenadas y:
m = 8 / (5 – 2)
Ahora resta las coordenadas x:
m = 8 / 3.
Así que, la pendiente de nuestra recta es 8/3. ¡Fácil, verdad?
Interpretando el Resultado
Ahora que tenemos la pendiente, es importante entender qué significa. Una pendiente de 8/3 significa que por cada 3 unidades que avanzamos horizontalmente (en el eje x), subimos 8 unidades verticalmente (en el eje y). Esto puede parecer mucho, pero recuerda que las pendientes pueden ser tanto positivas como negativas. Si tuviéramos una pendiente negativa, eso significaría que la línea baja a medida que te mueves hacia la derecha. Es como bajar una colina, ¿no?
Ejemplos Prácticos
Vamos a ver algunos ejemplos prácticos para que esto quede aún más claro. Imagina que tienes otra línea que pasa por los puntos C (1, 2) y D (4, 5). ¿Cómo calcularías la pendiente? Primero, identifica los puntos:
x₁ = 1, y₁ = 2, x₂ = 4, y₂ = 5.
Luego, usando la fórmula:
m = (5 – 2) / (4 – 1)
m = 3 / 3 = 1.
Esto significa que por cada unidad que avanzas a la derecha, subes una unidad. ¡Es una línea diagonal perfecta!
¿Qué Sucede con Líneas Verticales y Horizontales?
Es crucial saber que las líneas verticales y horizontales tienen pendientes especiales. Una línea horizontal, como una carretera plana, tiene una pendiente de 0 porque no sube ni baja. Por otro lado, una línea vertical tiene una pendiente indefinida porque no puedes dividir por cero. Esto es algo a tener en cuenta cuando trabajas con gráficos.
Aplicaciones de la Pendiente
La pendiente no solo es un concepto matemático; tiene aplicaciones en la vida real. Por ejemplo, en la economía, se usa para analizar la relación entre la oferta y la demanda. En la física, describe cómo cambian la velocidad y la posición. ¿Alguna vez has pensado en cómo la pendiente de una carretera afecta la velocidad de un coche? Es un ejemplo perfecto de cómo este concepto se entrelaza con nuestra vida diaria.
Ejercicios Prácticos para Practicar
Ahora que ya tienes una buena comprensión de cómo calcular la pendiente, ¿por qué no intentas algunos ejercicios por tu cuenta? Aquí hay algunos puntos para que practiques:
1. Puntos E (3, 7) y F (6, 10).
2. Puntos G (0, 0) y H (4, -4).
3. Puntos I (1, 5) y J (2, 5).
Intenta calcular la pendiente de cada uno de estos pares de puntos y luego compara tus respuestas. ¿Cuánto te ha ayudado practicar?
Calcular la pendiente de una recta puede parecer complicado al principio, pero con práctica y comprensión, se vuelve mucho más fácil. Ya sea que estés en la escuela, trabajando en un proyecto o simplemente tratando de entender mejor el mundo que te rodea, saber cómo calcular la pendiente es una habilidad valiosa. Así que la próxima vez que veas una recta en un gráfico, ¡recuerda que tienes las herramientas para entender su inclinación!
¿Qué pasa si los puntos son iguales?
Si los puntos son iguales, no puedes calcular la pendiente porque no hay cambio en las coordenadas. Esto resulta en una división por cero, lo que significa que la pendiente es indefinida.
¿Cómo se relaciona la pendiente con la ecuación de la recta?
La pendiente se relaciona directamente con la forma de la ecuación de la recta. En la forma y = mx + b, «m» es la pendiente y «b» es la intersección en el eje y. Esto significa que puedes usar la pendiente para escribir la ecuación de una recta si conoces un punto en ella.
¿Puedo tener una pendiente negativa y positiva al mismo tiempo?
No, cada línea tiene una única pendiente en un momento dado. Sin embargo, puedes tener diferentes segmentos de una gráfica que tengan pendientes positivas y negativas. Piensa en una montaña rusa que sube y baja; cada sección tiene su propia pendiente.
¿Por qué es importante entender la pendiente en la vida real?
Entender la pendiente en la vida real es esencial porque nos ayuda a interpretar datos y tomar decisiones informadas. Por ejemplo, si estás analizando el rendimiento de una inversión, la pendiente puede indicar si está creciendo o disminuyendo.