Cuando hablamos de extremos relativos en matemáticas, nos referimos a esos puntos especiales en una función donde se alcanza un máximo o un mínimo local. Pero, ¿qué significa eso exactamente? Imagina que estás escalando una montaña. Los picos representan los máximos, mientras que los valles representan los mínimos. Entender cómo identificar estos puntos puede ayudarte no solo en matemáticas, sino también en áreas como la economía, la física y la ingeniería. Así que, ¡prepárate para sumergirte en este viaje matemático! En esta guía, te mostraré un enfoque paso a paso para calcular extremos relativos, desglosando cada parte del proceso para que sea fácil de seguir. ¿Listo? Vamos a ello.
¿Qué Son los Extremos Relativos?
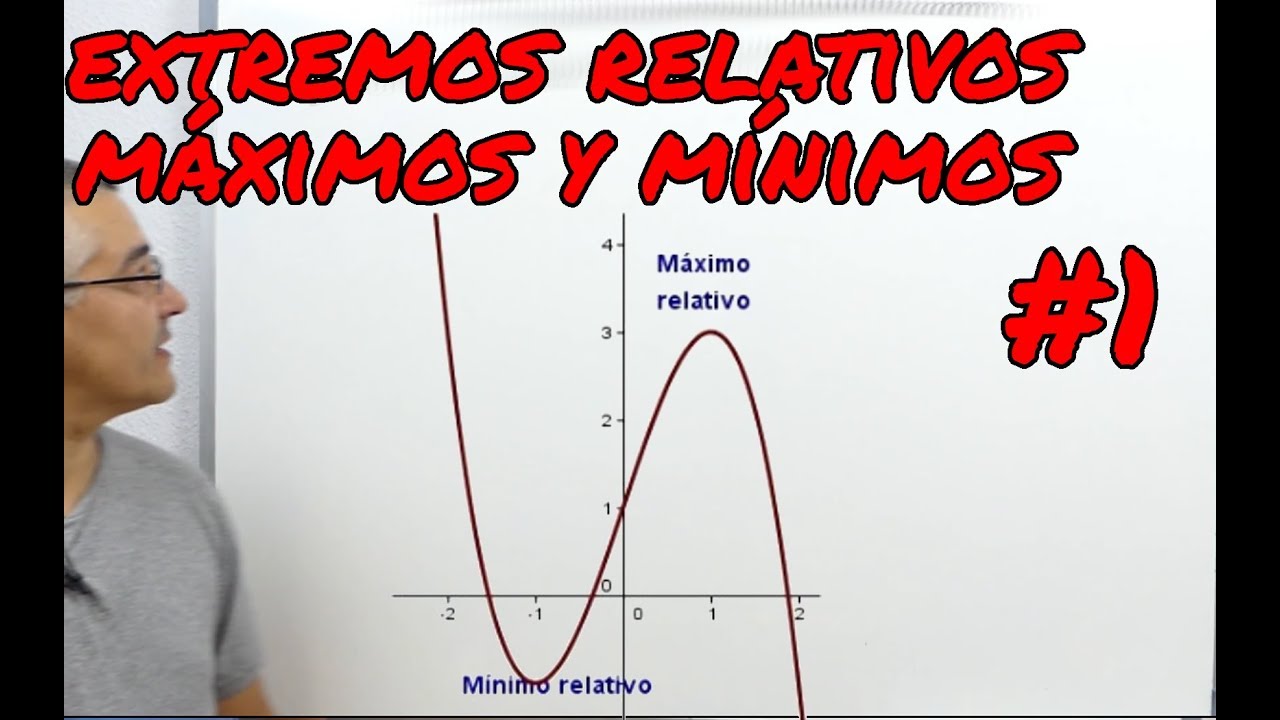
Antes de entrar en materia, es crucial que comprendas qué son realmente los extremos relativos. En términos simples, un extremo relativo (o local) de una función es un punto donde la función alcanza un valor mayor o menor que en sus alrededores. En otras palabras, es como encontrar un pequeño pico en una vasta llanura o un pequeño valle en una extensa colina. Los máximos relativos son puntos donde la función «sube» antes y «baja» después, mientras que los mínimos relativos son puntos donde la función «baja» antes y «sube» después. ¿Te imaginas caminando por un sendero montañoso y encontrando un lugar que es más alto que todos los puntos cercanos? Eso es un máximo relativo.
¿Por Qué Son Importantes los Extremos Relativos?
Identificar extremos relativos no es solo un ejercicio académico; tiene aplicaciones prácticas en el mundo real. Por ejemplo, en economía, los máximos pueden representar el precio más alto que los consumidores están dispuestos a pagar por un producto, mientras que los mínimos pueden indicar el costo más bajo de producción. En física, los extremos pueden ayudar a determinar las condiciones de equilibrio de un sistema. Así que, si alguna vez te has preguntado por qué deberías aprender esto, aquí tienes tu respuesta: ¡es fundamental para entender cómo funcionan las cosas en la vida real!
Pasos para Calcular Extremos Relativos
Paso 1: Encuentra la Derivada de la Función
El primer paso en nuestro viaje es encontrar la derivada de la función que estamos analizando. La derivada nos dará información sobre la tasa de cambio de la función. Piensa en ello como si estuvieras mirando la pendiente de una carretera: si la pendiente es positiva, estás subiendo; si es negativa, estás bajando. Para encontrar la derivada, simplemente aplica las reglas básicas de derivación. Por ejemplo, si tienes la función f(x) = x², la derivada sería f'(x) = 2x. ¿Ves cómo esto comienza a tomar forma?
Paso 2: Igualar la Derivada a Cero
Una vez que tengas la derivada, el siguiente paso es igualarla a cero. Esto se debe a que los extremos relativos ocurren donde la pendiente es cero, es decir, donde la función deja de subir o bajar. Siguiendo nuestro ejemplo anterior, si igualamos 2x a cero, obtenemos x = 0. Este es un candidato para ser un extremo relativo. Pero espera, ¡aún no hemos terminado!
Paso 3: Determinar la Naturaleza del Extremo
Ahora que tenemos un posible extremo relativo, debemos averiguar si es un máximo o un mínimo. Para ello, utilizamos la segunda derivada de la función. Si la segunda derivada es positiva en el punto crítico, entonces tenemos un mínimo relativo. Si es negativa, entonces es un máximo. En nuestro caso, la segunda derivada de f(x) = x² es f»(x) = 2, que es positiva. ¡Eso significa que tenemos un mínimo relativo en x = 0!
Paso 4: Evaluar los Límites
Además de la segunda derivada, también es útil evaluar la función en puntos cercanos al extremo. Esto te dará una idea más clara de cómo se comporta la función alrededor de ese punto. Imagina que estás haciendo una prueba de sabor: pruebas un poco de la comida alrededor de un plato para asegurarte de que sea realmente bueno. Al evaluar la función en valores como -1 y 1, puedes observar que efectivamente tienes un mínimo en x = 0.
Paso 5: Conclusiones y Gráfica
Finalmente, es una buena práctica graficar la función. Esto no solo te ayuda a visualizar los extremos, sino que también te da una representación clara de cómo se comporta la función en general. Puedes usar herramientas como Desmos o GeoGebra para graficar fácilmente. Al observar la gráfica, podrás ver claramente el mínimo en x = 0 y cómo la función se comporta en sus alrededores. ¿No es genial poder ver lo que has calculado?
Ejemplo Práctico
Vamos a poner en práctica lo que hemos aprendido. Supongamos que queremos encontrar los extremos relativos de la función f(x) = -x³ + 3x² + 2. Primero, encontramos la derivada: f'(x) = -3x² + 6x. Igualamos a cero: -3x² + 6x = 0, lo que nos da x(6 – 3x) = 0, así que x = 0 y x = 2 son nuestros puntos críticos. Ahora, calculamos la segunda derivada: f»(x) = -6x + 6. Evaluamos en nuestros puntos críticos: f»(0) = 6 (positivo, por lo que x = 0 es un mínimo) y f»(2) = -6 (negativo, por lo que x = 2 es un máximo). Al graficar la función, podrás ver claramente estos extremos. ¡Así de fácil!
Errores Comunes y Consejos
Algunos estudiantes pueden cometer errores comunes al calcular extremos relativos. Uno de los más frecuentes es olvidar verificar la segunda derivada o no evaluar los límites cercanos. Recuerda que los extremos relativos no son solo números; son puntos en una función que tienen un significado. Así que tómate tu tiempo, verifica tus cálculos y no dudes en graficar para asegurarte de que todo tiene sentido.
¿Los extremos relativos siempre son máximos o mínimos globales?
No, los extremos relativos son solo máximos o mínimos en una vecindad específica, no necesariamente en toda la función. Un máximo o mínimo global es el más alto o más bajo de toda la función.
¿Cómo se relacionan los extremos relativos con la continuidad de la función?
Los extremos relativos pueden existir en funciones continuas, pero no todas las funciones continuas tienen extremos. Sin embargo, si una función es continua y está definida en un intervalo cerrado, entonces debe tener al menos un máximo y un mínimo.
¿Se pueden encontrar extremos relativos en funciones no diferenciables?
En general, los extremos relativos se encuentran en funciones diferenciables. Sin embargo, hay excepciones donde las funciones pueden tener extremos en puntos no diferenciables, como los picos o «esquinas». En esos casos, se debe evaluar la función directamente.
¿Qué pasa si la derivada no se puede igualar a cero?
Si la derivada nunca se iguala a cero, eso significa que la función no tiene extremos relativos en ese intervalo. En otras palabras, la función podría ser creciente o decreciente en todo el intervalo.
¿Puedo usar calculadoras gráficas para encontrar extremos?
¡Definitivamente! Las calculadoras gráficas y software matemático son herramientas excelentes para visualizar funciones y encontrar extremos relativos de manera rápida y precisa.
En conclusión, calcular extremos relativos es una habilidad fundamental en matemáticas que te permitirá analizar y comprender mejor las funciones. Siguiendo estos pasos y practicando con ejemplos, te convertirás en un experto en poco tiempo. Así que, ¡sigue practicando y no dudes en explorar más allá de los límites de las matemáticas!