Explorando la Bisectriz: Un Viaje Matemático
¡Hola! Hoy vamos a sumergirnos en un tema fascinante que a menudo se pasa por alto en el mundo de las matemáticas: la bisectriz del segundo cuadrante. Si alguna vez te has preguntado cómo funciona, por qué es importante y cómo se aplica en la vida real, ¡estás en el lugar correcto! La bisectriz, en términos sencillos, es una línea que divide un ángulo en dos partes iguales. Pero, ¿qué pasa cuando hablamos específicamente del segundo cuadrante? Antes de que te sientas abrumado, respira hondo y acompáñame en este recorrido. Te prometo que será interesante y, sobre todo, útil.
¿Qué es el Segundo Cuadrante?
Para entender la bisectriz en el segundo cuadrante, primero debemos saber qué es un cuadrante. Imagina el plano cartesiano, ese que todos hemos visto en clase de matemáticas, con su eje X y eje Y. Este plano se divide en cuatro partes, llamadas cuadrantes. El segundo cuadrante se encuentra en la parte superior izquierda, donde los valores de X son negativos y los valores de Y son positivos. Piensa en ello como un mapa: el segundo cuadrante es la zona donde los puntos se sitúan a la izquierda del origen y por encima del eje X.
Características del Segundo Cuadrante
Una de las características más interesantes del segundo cuadrante es cómo afecta a las funciones trigonométricas. Si piensas en un círculo unitario, todos los ángulos que caen en este cuadrante tienen un seno positivo (que se relaciona con el eje Y) y un coseno negativo (que se relaciona con el eje X). Esto significa que, en este cuadrante, los valores de las funciones trigonométricas se comportan de manera diferente en comparación con otros cuadrantes. ¡Es un mundo fascinante!
La Bisectriz en el Segundo Cuadrante
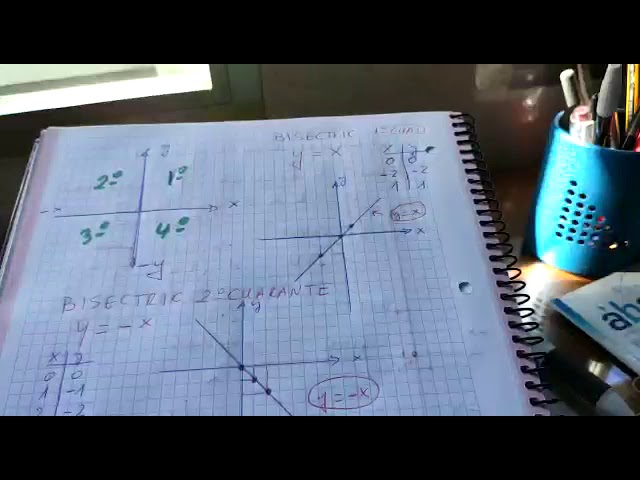
Ahora que tenemos una idea clara de qué es el segundo cuadrante, hablemos de la bisectriz. La bisectriz de un ángulo es la línea que lo divide en dos partes iguales. En el segundo cuadrante, la bisectriz de un ángulo se extiende desde el vértice del ángulo y se dirige hacia el exterior, cruzando el eje Y y el eje X. Esto crea dos ángulos que son congruentes, lo que significa que tienen la misma medida. Pero, ¿por qué debería importarnos esto?
Importancia de la Bisectriz
La bisectriz tiene aplicaciones prácticas en diversos campos. Por ejemplo, en la arquitectura, se utiliza para garantizar que las estructuras sean simétricas. En la navegación, ayuda a los marineros a determinar direcciones precisas. Además, en la geometría, la bisectriz es fundamental para resolver problemas de construcción y diseño. Así que, la próxima vez que veas una bisectriz, recuerda que no es solo una línea; es una herramienta poderosa.
Propiedades de la Bisectriz
Hablemos ahora de algunas propiedades clave de la bisectriz que pueden ayudarte a entender su funcionamiento. Una de las propiedades más interesantes es que, en un triángulo, la bisectriz de un ángulo divide el lado opuesto en segmentos que son proporcionales a los otros dos lados del triángulo. Esto se conoce como el teorema de la bisectriz. Si alguna vez has estado en un triángulo y has querido encontrar la longitud de un lado, este teorema es tu mejor amigo.
Ejemplo Práctico del Teorema de la Bisectriz
Imagina que tienes un triángulo con lados de longitud 6 y 8. Si dibujas la bisectriz desde el ángulo opuesto a la base, esta dividirá el lado de la base en dos partes. Si llamamos a esas partes «a» y «b», entonces podemos decir que:
a/b = 6/8
Esto significa que puedes encontrar la longitud de «a» y «b» si conoces la longitud de la base. ¿No es genial? Así que, la próxima vez que estés en una situación en la que necesites medir algo, recuerda que la bisectriz puede ser tu aliada.
Aplicaciones en la Vida Real
Hablemos de cómo la bisectriz del segundo cuadrante se aplica en la vida cotidiana. Desde la planificación urbana hasta el diseño de productos, la geometría juega un papel crucial. Por ejemplo, cuando los arquitectos diseñan edificios, utilizan bisectrices para crear planos simétricos y equilibrados. Esto no solo se ve bien, sino que también asegura que la estructura sea fuerte y duradera.
Además, en la navegación, los capitanes de barco utilizan la bisectriz para calcular rutas. Al trazar un curso en un mapa, la bisectriz les ayuda a determinar la dirección más corta entre dos puntos, lo que ahorra tiempo y recursos. Así que, cuando pienses en viajar, recuerda que las matemáticas están en juego, incluso si no lo notas.
Desafíos y Problemas Comunes
A pesar de todas sus ventajas, trabajar con bisectrices no siempre es fácil. Muchos estudiantes se sienten intimidados por las matemáticas, especialmente cuando se trata de geometría. Pero aquí está la clave: la práctica hace al maestro. Si te enfrentas a un problema que involucra bisectrices, no te desanimes. Empieza por descomponer el problema en pasos más pequeños. Dibuja un diagrama y utiliza tus conocimientos sobre proporciones y ángulos. Con el tiempo, te volverás más confiado y competente.
Errores Comunes
Un error común que muchos cometen es olvidar que la bisectriz no solo divide el ángulo en dos partes iguales, sino que también tiene propiedades relacionadas con los lados del triángulo. Así que, si estás trabajando en un problema, asegúrate de recordar estas propiedades. ¡Te sorprenderás de lo mucho que pueden ayudarte!
¿Qué es una bisectriz?
Una bisectriz es una línea que divide un ángulo en dos partes iguales. En geometría, es fundamental para resolver problemas relacionados con triángulos y otras figuras.
¿Por qué es importante la bisectriz en el segundo cuadrante?
La bisectriz en el segundo cuadrante ayuda a entender cómo se comportan las funciones trigonométricas y se aplica en diversas disciplinas, desde la arquitectura hasta la navegación.
¿Cómo se calcula la longitud de una bisectriz?
Para calcular la longitud de una bisectriz en un triángulo, puedes usar el teorema de la bisectriz, que relaciona las longitudes de los lados con los segmentos que se crean en el lado opuesto.
¿La bisectriz tiene aplicaciones en la vida real?
Sí, la bisectriz se utiliza en diversas áreas, como la arquitectura, el diseño urbano y la navegación, para crear estructuras equilibradas y determinar rutas eficientes.
¿Qué errores debo evitar al trabajar con bisectrices?
Evita olvidar las propiedades de la bisectriz en relación con los lados del triángulo y asegúrate de practicar con ejemplos para mejorar tu comprensión.
Así que ahí lo tienes, un recorrido completo por la bisectriz del segundo cuadrante. Espero que hayas disfrutado este viaje tanto como yo. ¿Tienes alguna pregunta o quieres profundizar en algún aspecto en particular? ¡No dudes en comentar!