Las asintotas son conceptos fascinantes en el mundo del análisis matemático, y su comprensión puede abrirte las puertas a una mejor interpretación de las funciones. Pero, ¿qué son exactamente las asintotas? Imagina que estás conduciendo por una carretera que parece no tener fin. A medida que avanzas, te das cuenta de que hay ciertos puntos en los que la carretera se aproxima a una línea, pero nunca la toca. Esa es la esencia de las asintotas. En términos matemáticos, una asintota es una línea que se aproxima a una curva, y puede ser vertical, horizontal o incluso oblicua. En este artículo, exploraremos a fondo las asintotas horizontales y verticales, con ejemplos y aplicaciones que te ayudarán a entender su relevancia.
## ¿Qué son las asintotas horizontales?
Las asintotas horizontales son líneas en el eje Y que describen el comportamiento de una función a medida que la variable independiente se aproxima a infinito o menos infinito. ¿Te suena complicado? No te preocupes, es más sencillo de lo que parece. Cuando decimos que una función tiene una asintota horizontal, estamos hablando de que, a medida que «x» se vuelve muy grande (positivo o negativo), el valor de la función se aproxima a un número constante. Por ejemplo, si tenemos la función (f(x) = frac{1}{x}), cuando «x» se vuelve muy grande, (f(x)) se aproxima a 0. En este caso, la línea (y = 0) es una asintota horizontal.
### Ejemplos de asintotas horizontales
Para entender mejor este concepto, veamos un par de ejemplos:
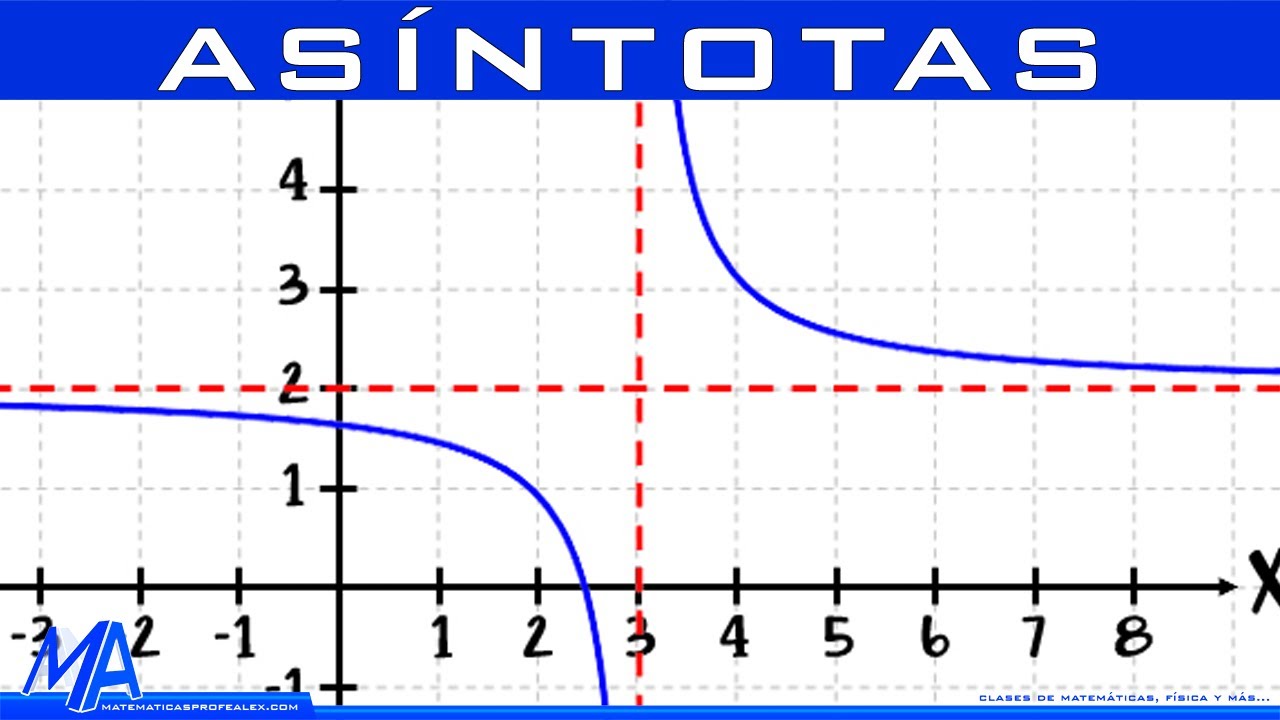
1. Función racional: Consideremos la función (f(x) = frac{2x + 3}{x + 1}). Si evaluamos esta función cuando «x» se acerca a infinito, los términos de mayor grado (2x y x) dominan, lo que nos lleva a decir que (f(x) approx 2). Por lo tanto, la asintota horizontal es (y = 2).
2. Función exponencial: Ahora, tomemos la función (g(x) = e^{-x}). A medida que «x» se hace muy grande, (g(x)) se aproxima a 0. Por lo tanto, en este caso, también tenemos una asintota horizontal en (y = 0).
## ¿Qué son las asintotas verticales?
Por otro lado, las asintotas verticales son líneas en el eje X donde la función tiende a infinito. Es como si la carretera que mencionamos antes se detuviera abruptamente, y al acercarte, te das cuenta de que la función se dispara a valores extremadamente altos o bajos. Generalmente, las asintotas verticales ocurren en puntos donde la función no está definida, como divisiones por cero. Por ejemplo, en la función (h(x) = frac{1}{x-2}), hay una asintota vertical en (x = 2), porque al sustituir 2 en el denominador, la función se vuelve indefinida.
### Ejemplos de asintotas verticales
Vamos a explorar algunos ejemplos para que quede más claro:
1. Función racional: Considera la función (f(x) = frac{1}{x^2 – 4}). Aquí, el denominador se vuelve cero cuando (x = 2) o (x = -2). Por lo tanto, tenemos dos asintotas verticales en (x = 2) y (x = -2).
2. Función logarítmica: Tomemos (g(x) = ln(x – 1)). Esta función no está definida para (x leq 1), así que hay una asintota vertical en (x = 1). Al acercarse a este valor, la función se va a menos infinito.
## Cómo encontrar asintotas: Un enfoque paso a paso
Ahora que hemos cubierto qué son las asintotas y hemos visto algunos ejemplos, es hora de aprender cómo encontrarlas. Vamos a desglosar el proceso en pasos sencillos.
### Encontrar asintotas horizontales
1. Identifica el tipo de función: Asegúrate de que estás trabajando con una función racional o una función que tiende a un límite.
2. Evalúa el límite: Calcula el límite de la función cuando «x» tiende a infinito y menos infinito. Puedes usar técnicas de factorización o dividir entre el término de mayor grado en el numerador y denominador.
3. Determina la asintota: Si el límite resulta en un número constante, esa será tu asintota horizontal.
### Encontrar asintotas verticales
1. Busca puntos de discontinuidad: Identifica los valores de «x» que hacen que el denominador sea cero.
2. Evalúa el comportamiento cerca de esos puntos: Analiza el comportamiento de la función al acercarte a esos valores desde la izquierda y la derecha. Si la función tiende a infinito positivo o negativo, tienes una asintota vertical.
## Aplicaciones de las asintotas
Las asintotas no son solo un tema académico; tienen aplicaciones prácticas en diversas áreas. Desde la ingeniería hasta la economía, entender el comportamiento de las funciones a través de asintotas puede ser extremadamente útil.
### En ingeniería
Imagina que estás diseñando un puente. Necesitas asegurarte de que la estructura sea estable a diferentes cargas. Las asintotas pueden ayudarte a entender cómo se comportará la carga en el puente bajo diferentes condiciones. Al analizar las funciones que describen la tensión y la compresión, puedes predecir comportamientos extremos y asegurarte de que tu diseño sea seguro.
### En economía
En el ámbito económico, las asintotas pueden ser útiles para modelar costos y beneficios. Por ejemplo, al analizar la función de producción, puedes identificar límites en la producción a medida que se añaden más recursos. Esto puede ayudar a los gerentes a tomar decisiones informadas sobre la asignación de recursos.
## Conclusión
Las asintotas, tanto horizontales como verticales, son herramientas esenciales en el análisis de funciones. Te permiten entender el comportamiento de las funciones en los extremos y en puntos críticos. Si bien pueden parecer un concepto complicado al principio, con práctica y un enfoque paso a paso, puedes dominarlas. Así que la próxima vez que te encuentres con una función, pregúntate: ¿dónde están sus asintotas? ¿Qué me están diciendo sobre su comportamiento?
### Preguntas Frecuentes
1. ¿Todas las funciones tienen asintotas?
No, no todas las funciones tienen asintotas. Las asintotas son comunes en funciones racionales, pero algunas funciones pueden no tener asintotas en absoluto.
2. ¿Puede una función tener más de una asintota horizontal?
No, una función solo puede tener una asintota horizontal. Esto se debe a que a medida que «x» se aproxima a infinito, el valor de la función se estabiliza en un solo número.
3. ¿Cómo se relacionan las asintotas con el gráfico de la función?
Las asintotas actúan como guías para el comportamiento del gráfico de la función. Te ayudan a visualizar cómo se comporta la función en los extremos y en puntos donde no está definida.
4. ¿Qué pasa si una función toca su asintota?
Si una función toca su asintota, esto generalmente significa que la función se comporta de manera diferente en esa área y puede no tener una asintota en ese punto. En tal caso, es necesario analizar más a fondo la función.
5. ¿Son las asintotas importantes en la vida real?
Sí, las asintotas son muy importantes en aplicaciones prácticas, como la ingeniería y la economía, ya que ayudan a modelar y predecir comportamientos en situaciones extremas.
¡Y ahí lo tienes! Una guía completa sobre asintotas horizontales y verticales. Espero que ahora tengas una mejor comprensión de este fascinante tema. ¿Listo para aplicar lo que has aprendido?