Entendiendo la Geometría de los Vectores
¿Alguna vez te has preguntado cómo los matemáticos logran calcular áreas de formas geométricas de una manera tan elegante? Hoy, vamos a adentrarnos en el fascinante mundo de los triángulos y cómo podemos usar vectores para calcular su área. Imagina que los vectores son como flechas en el espacio; cada uno tiene una dirección y una longitud. Al juntar estos vectores, podemos formar triángulos y, con un poco de matemáticas, podemos descubrir cuánto espacio ocupan.
Calcular el área de un triángulo utilizando vectores es un método que puede parecer un poco complicado al principio, pero te prometo que, una vez que lo entiendas, te sentirás como un verdadero matemático. Así que, prepárate para una aventura matemática donde desglosaremos este proceso paso a paso. Primero, vamos a recordar algunas propiedades básicas de los triángulos y de los vectores.
¿Qué es un Triángulo?
Un triángulo es una figura geométrica que tiene tres lados y tres ángulos. Puede ser escaleno, isósceles o equilátero, dependiendo de la longitud de sus lados. Pero, ¿qué pasa si queremos calcular su área? Aquí es donde entran los vectores. Un triángulo puede ser definido por sus vértices en un plano cartesiano, lo que nos lleva a la siguiente pregunta: ¿cómo podemos usar estos vértices para calcular el área?
Definiendo Vectores
Los vectores son entidades matemáticas que tienen magnitud y dirección. En un sistema de coordenadas, un vector puede ser representado por sus componentes en los ejes X y Y. Por ejemplo, un vector que va del origen (0,0) a un punto (x,y) puede ser representado como v = (x, y).
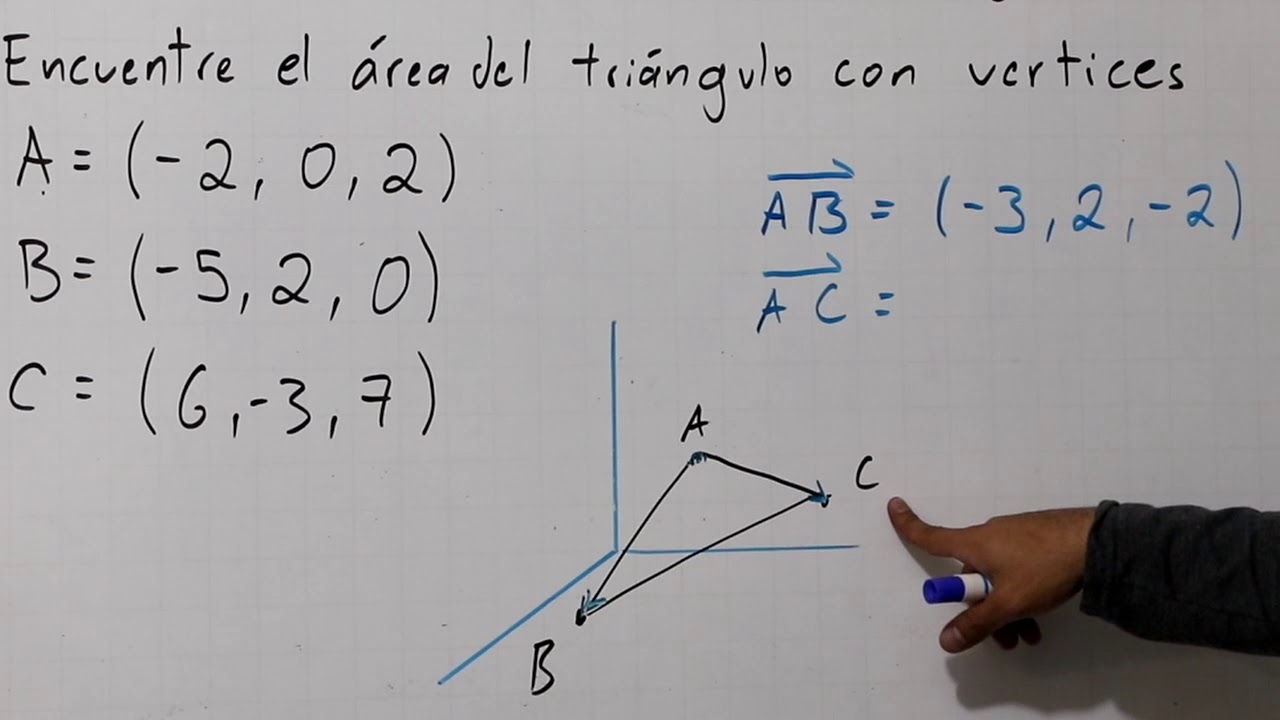
Para calcular el área de un triángulo, necesitamos tres vértices. Supongamos que tenemos tres puntos en el plano: A(x1, y1), B(x2, y2) y C(x3, y3). Podemos definir dos vectores que se originen en uno de estos vértices. Digamos que elegimos el punto A. Los vectores serían:
– AB = (x2 – x1, y2 – y1)
– AC = (x3 – x1, y3 – y1)
¿Ves cómo estos vectores nos ayudan a visualizar la forma del triángulo? Ahora, vamos a usar estos vectores para calcular el área.
Fórmula del Área Usando Vectores
La fórmula para calcular el área de un triángulo formado por dos vectores es:
Área = 0.5 * |AB × AC|
Donde × representa el producto cruzado. El producto cruzado de dos vectores en el espacio bidimensional se puede calcular usando la siguiente fórmula:
AB × AC = (x2 – x1)(y3 – y1) – (y2 – y1)(x3 – x1)
Esta fórmula nos da el valor absoluto del determinante de la matriz formada por las componentes de los vectores, lo que a su vez nos da el área del triángulo.
Ejemplo Práctico
Para hacer esto más claro, veamos un ejemplo práctico. Supongamos que tenemos los puntos A(1, 2), B(4, 6) y C(5, 2).
Primero, calculamos los vectores:
– AB = (4 – 1, 6 – 2) = (3, 4)
– AC = (5 – 1, 2 – 2) = (4, 0)
Ahora, aplicamos la fórmula del producto cruzado:
AB × AC = (3)(0) – (4)(4) = 0 – 16 = -16
Tomamos el valor absoluto:
|AB × AC| = 16
Finalmente, calculamos el área:
Área = 0.5 * 16 = 8
Así que, el área del triángulo formado por los puntos A, B y C es 8 unidades cuadradas. ¡Fácil, verdad?
Visualizando el Proceso
Ahora que hemos recorrido el camino de los cálculos, es importante visualizarlo. Imagina que estás dibujando el triángulo en un papel. Trazas los puntos A, B y C y luego dibujas las flechas que representan los vectores AB y AC. Al hacer esto, puedes ver cómo se forma el triángulo y cómo los vectores ayudan a definir su forma.
Además, si alguna vez has jugado con un rompecabezas, piensa en cómo encajan las piezas. Los vectores son como esas piezas; cuando las unes correctamente, forman algo completo y hermoso.
¿Por Qué Usar Vectores?
Puede que te preguntes, ¿por qué usar vectores en lugar de las fórmulas tradicionales para calcular el área de un triángulo? Bueno, hay varias razones. Primero, el uso de vectores simplifica muchos problemas en geometría y física. Te permite trabajar con coordenadas de una manera más flexible y visual. Además, en contextos más avanzados, como en la física o la ingeniería, los vectores son fundamentales para describir movimientos y fuerzas.
Calcular el área de un triángulo usando vectores es una técnica poderosa que no solo te ayuda a entender mejor la geometría, sino que también te prepara para desafíos más complejos en matemáticas y ciencias. A medida que te familiarices con este enfoque, te darás cuenta de que los vectores son tus amigos en el mundo de las matemáticas.
¿Puedo usar vectores para calcular el área de triángulos en tres dimensiones?
¡Claro! El concepto se extiende fácilmente a tres dimensiones usando vectores en el espacio. Solo necesitas tres puntos y calcular el producto cruzado en 3D.
¿Qué pasa si los puntos son colineales?
Si los puntos son colineales, el área del triángulo será cero, ya que no formarán un triángulo real.
¿Hay otras formas de calcular el área de un triángulo?
Sí, puedes usar la base y la altura, o la fórmula de Herón si conoces las longitudes de los lados.
¿Los vectores son útiles en otras áreas de las matemáticas?
Definitivamente. Los vectores son fundamentales en álgebra lineal, cálculo y física, entre otras disciplinas.
¿Cómo puedo practicar más sobre el uso de vectores?
Puedes intentar resolver problemas en libros de texto, o incluso crear tus propios triángulos y calcular su área usando vectores. ¡La práctica hace al maestro!
Espero que este artículo te haya proporcionado una visión clara y accesible sobre cómo calcular el área de un triángulo usando vectores. ¡Diviértete explorando las matemáticas!