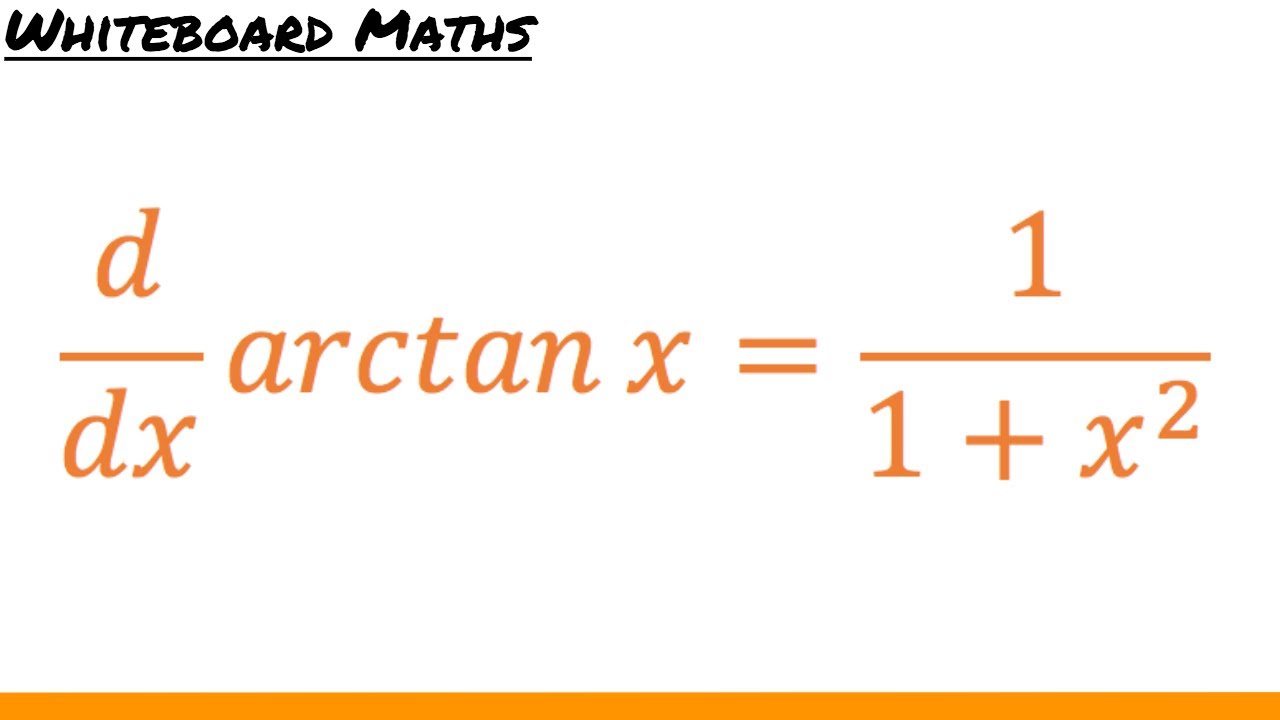¿Qué es la función Arctan y por qué es importante?
La función arctangente, comúnmente abreviada como arctan, es una de las funciones trigonométricas inversas más útiles en matemáticas. Si alguna vez te has preguntado cómo encontrar el ángulo cuya tangente es un número dado, ¡estás en el lugar correcto! Esta función se utiliza en una variedad de campos, desde la física hasta la ingeniería y la estadística. Pero, ¿sabías que la derivada de esta función también tiene un papel crucial en el cálculo y en la resolución de problemas más complejos? En este artículo, vamos a desglosar la derivada de la función arctan de una manera sencilla y comprensible. Te prometo que, al final de esta lectura, te sentirás mucho más cómodo con el tema y podrás aplicarlo en tus propios estudios o proyectos.
La derivada de la función arctan(x) es un concepto fundamental que te ayudará a entender cómo cambia la función en relación a su variable independiente, x. La buena noticia es que la derivada de arctan(x) es bastante simple y elegante. Se expresa como:
f'(x) = 1 / (1 + x²).
Esto significa que, a medida que x varía, la pendiente de la función arctan se puede calcular fácilmente utilizando esta fórmula. Pero, ¿qué significa esto en términos prácticos? Imagina que estás en una montaña y quieres saber qué tan empinada es la subida en un punto específico. La derivada te dirá exactamente eso: cuán rápido cambia la altura de la montaña en ese punto.
Fundamentos de la Derivada
Antes de sumergirnos en los detalles de la derivada de arctan, es importante repasar qué es una derivada en primer lugar. La derivada mide cómo cambia una función en relación a su variable. En términos simples, es la tasa de cambio de una función. Si piensas en una carretera en la que conduces, la derivada te diría qué tan inclinada es la carretera en un punto específico. Así, cuando hablamos de la derivada de arctan, estamos hablando de cómo cambia el ángulo en función del valor de la tangente.
La derivada se puede entender también como la pendiente de la tangente a la curva de la función en un punto dado. Si dibujas la gráfica de arctan(x), notarás que se aproxima a 90 grados (π/2) a medida que x se vuelve muy grande y a -90 grados (-π/2) cuando x se vuelve muy negativo. Esto significa que la función tiene límites en ambos extremos, lo que también afecta su derivada. En otras palabras, aunque la función arctan sigue creciendo, lo hace de manera cada vez más lenta, lo que se refleja en la disminución de la pendiente de su derivada.
Derivación de la Función Arctan
Ahora, vamos a ver cómo se obtiene la derivada de la función arctan. Para ello, utilizaremos la regla de la derivada de una función compuesta. La derivada de la función arctan se puede encontrar utilizando la definición de la derivada o aplicando reglas de derivación conocidas. Si deseas un enfoque más técnico, aquí va:
1. Empezamos con la definición de la función:
f(x) = arctan(x).
2. Utilizamos la regla de la cadena:
La derivada de arctan(u) con respecto a x, donde u es una función de x, se puede calcular como:
f'(x) = (1 / (1 + u²)) * (du/dx).
3. Para nuestra función, u es simplemente x:
Así que, al derivar, tenemos:
f'(x) = (1 / (1 + x²)) * (d(x)/dx) = 1 / (1 + x²).
Y ahí lo tienes. La derivada de la función arctan(x) es simplemente 1 / (1 + x²). Este resultado es asombroso porque no solo es simple, sino que también nos da información valiosa sobre la función.
Ejemplos Prácticos
Para entender mejor cómo funciona esto, veamos algunos ejemplos prácticos.
Ejemplo 1: Derivada en un punto específico
Supongamos que queremos encontrar la derivada de arctan en x = 1. Usamos nuestra fórmula:
f'(1) = 1 / (1 + 1²) = 1 / (1 + 1) = 1 / 2.
Esto significa que en x = 1, la pendiente de la curva de arctan es 1/2. En otras palabras, si dibujas la gráfica de arctan, en ese punto específico, la inclinación es bastante suave.
Ejemplo 2: Comportamiento en los extremos
Ahora, veamos qué sucede cuando x se aproxima a infinito.
f'(∞) = 1 / (1 + ∞²) = 1 / ∞ = 0.
Esto indica que, a medida que x se hace muy grande, la pendiente de la función arctan se aproxima a cero. Así que, aunque la función sigue aumentando, lo hace de manera cada vez más lenta.
Propiedades de la Derivada de Arctan
Es importante no solo conocer cómo calcular la derivada, sino también entender algunas propiedades interesantes que la rodean.
Continuidad y Diferenciabilidad
La función arctan(x) es continua y diferenciable en todo su dominio, que es el conjunto de todos los números reales. Esto significa que no hay «saltos» o «interrupciones» en la función, lo que facilita su análisis.
Monotonía
La derivada de arctan(x) siempre es positiva para todos los valores de x. Esto implica que la función arctan es monótona creciente. En otras palabras, a medida que x aumenta, arctan(x) también aumenta. ¡No hay forma de que la función baje!
Límites en los extremos
Como mencionamos anteriormente, a medida que x tiende a infinito, arctan(x) se aproxima a π/2. De igual manera, cuando x tiende a menos infinito, arctan(x) se aproxima a -π/2. Estos límites nos muestran que la función tiene un comportamiento predecible en los extremos.
Aplicaciones de la Derivada de Arctan
La derivada de la función arctan no es solo un concepto teórico; tiene aplicaciones prácticas en el mundo real. Aquí hay algunas áreas donde se utiliza:
Física
En física, la arctan se utiliza para calcular ángulos en problemas de trigonometría, especialmente en el contexto de la cinemática y la dinámica. La derivada puede ayudar a entender cómo varía la posición de un objeto en movimiento.
Ingeniería
Los ingenieros a menudo utilizan la arctan para modelar situaciones en las que se requiere el cálculo de ángulos en sistemas de control y robótica. La derivada de arctan puede ayudar a optimizar el rendimiento de estos sistemas.
Economía
En economía, los modelos que involucran tasas de cambio, como la elasticidad, a menudo utilizan funciones arctan. La derivada puede ayudar a determinar cómo cambia la demanda en respuesta a cambios en el precio.
¿La derivada de arctan(x) es siempre positiva?
Sí, la derivada de arctan(x) es siempre positiva para todos los valores de x, lo que significa que la función es monótona creciente.
¿Qué sucede con la derivada cuando x es cero?
Cuando x = 0, la derivada de arctan(0) es 1, lo que significa que la pendiente de la función en ese punto es bastante pronunciada.
¿Por qué es útil la derivada de arctan en la vida diaria?
La derivada de arctan tiene aplicaciones prácticas en campos como la física, la ingeniería y la economía, donde se requieren cálculos de ángulos y tasas de cambio.
¿Cómo se relaciona la derivada de arctan con otras funciones trigonométricas?
La derivada de arctan está relacionada con la función tangente, ya que arctan(x) es la función inversa de la tangente. Esto establece una conexión directa entre las tasas de cambio de ambas funciones.
¿Hay alguna regla específica para derivar funciones compuestas que incluyan arctan?
Sí, puedes usar la regla de la cadena para derivar funciones que incluyan arctan como parte de una función más grande. Recuerda que necesitas derivar tanto la función externa como la interna.
Así que ahí lo tienes, una guía completa sobre la derivada de la función arctan. Espero que te haya resultado útil y claro. ¡Ahora ve y pon en práctica lo que has aprendido! ¿Tienes alguna otra pregunta sobre este tema o algo relacionado? ¡Estoy aquí para ayudarte!