Cuando hablamos de geometría, es fácil sentir que estamos ante un universo lleno de formas y figuras que parecen tener vida propia. Uno de los conceptos más fascinantes que podemos encontrar en este mundo es el ángulo poliedro. Pero, ¿qué es exactamente? En términos simples, un ángulo poliedro se forma cuando se juntan tres o más caras planas en un vértice. Imagina que estás en un rincón de una habitación donde se encuentran las paredes; el espacio que se forma entre ellas es un ángulo poliedro. Este concepto no solo es fundamental en matemáticas, sino que también tiene aplicaciones en la arquitectura, la ingeniería y hasta en la naturaleza. En este artículo, desglosaremos su definición, propiedades y ofreceremos ejemplos que te ayudarán a entenderlo mejor.
Encabezado relacionado: La importancia del ángulo poliedro en la geometría
Definición del ángulo poliedro
Para profundizar en el tema, primero necesitamos definir qué es un poliedro. Un poliedro es un sólido tridimensional que tiene caras planas, aristas y vértices. Así que, cuando hablamos de un ángulo poliedro, nos referimos específicamente al espacio que se forma entre tres o más caras que se encuentran en un punto común, conocido como vértice. Este ángulo puede variar en tamaño dependiendo de cómo se posicionen las caras. Si alguna vez has visto un cubo, el espacio en cada esquina es un ángulo poliedro, y al mirar un tetraedro, que es el poliedro más simple, notarás que tiene cuatro caras triangulares y cuatro vértices, cada uno de los cuales forma un ángulo poliedro.
Propiedades del ángulo poliedro
Tipos de ángulos poliedros
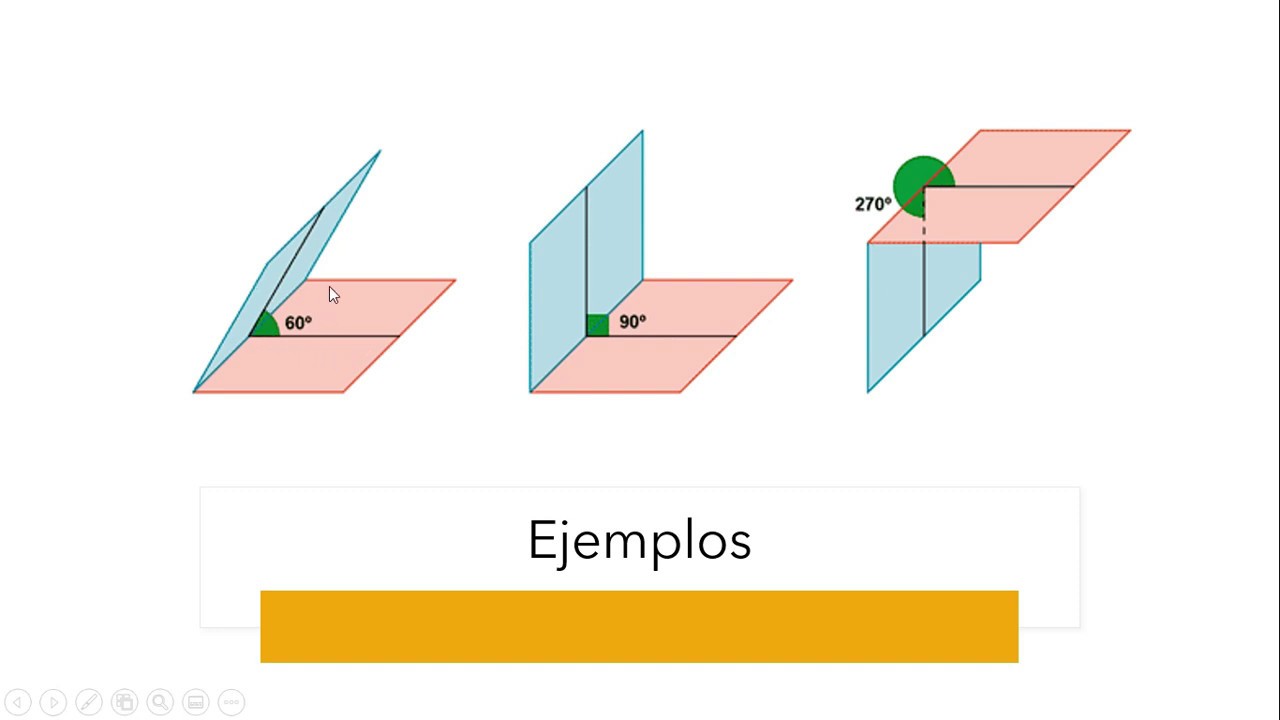
Los ángulos poliedros se pueden clasificar de varias maneras. Una de las más comunes es según su medida. Podemos encontrar ángulos poliedros agudos, rectos y obtusos. Los ángulos agudos son aquellos que miden menos de 90 grados, mientras que los rectos son exactamente 90 grados y los obtusos superan esta medida. Por otro lado, también podemos clasificar los ángulos poliedros en función del número de caras que los forman. Por ejemplo, un ángulo poliedro formado por tres caras se denomina triángulo, mientras que uno formado por cuatro caras se llama tetraédrico. Esta clasificación es útil para comprender mejor la variedad de formas que pueden tener los ángulos poliedros.
La suma de los ángulos poliedros
Una propiedad fascinante de los ángulos poliedros es que la suma de los ángulos en un poliedro siempre es menor que 360 grados. Esto se debe a que, a medida que se agregan más caras, el espacio que se forma en el vértice se reduce. Así que, si alguna vez te has preguntado cuántos grados puede abarcar un ángulo poliedro, la respuesta es que depende de cuántas caras lo rodean. Es como si cada vez que añadimos una cara nueva, estuviéramos cerrando un poco más el espacio. ¡Increíble, verdad?
Aplicaciones en la vida real
La importancia de los ángulos poliedros va más allá de la teoría matemática. Estos ángulos tienen aplicaciones prácticas en diversas áreas. Por ejemplo, en arquitectura, los arquitectos utilizan ángulos poliedros para diseñar estructuras estéticamente agradables y funcionales. En la ingeniería, el diseño de maquinaria y herramientas también se basa en estos ángulos para garantizar que se ensamblen correctamente. Incluso en la naturaleza, podemos ver ejemplos de ángulos poliedros en cristales, estructuras biológicas y en la forma en que se organizan ciertos organismos. Por lo tanto, comprender los ángulos poliedros no es solo un ejercicio académico, sino una habilidad esencial para muchas profesiones.
Ejemplos explicativos de ángulos poliedros
El cubo
Un ejemplo clásico de un ángulo poliedro es el cubo. Este sólido tiene seis caras cuadradas y ocho vértices. En cada vértice, se encuentran tres caras, formando un ángulo recto. Al observar un cubo, puedes notar cómo las caras se unen en los vértices para crear esos ángulos poliedros. Es un gran ejemplo para visualizar este concepto en acción.
El tetraedro
Pasemos ahora al tetraedro, que es el poliedro más simple. Tiene cuatro caras triangulares y cuatro vértices. En cada vértice se unen tres caras, formando un ángulo poliedro. Es interesante notar que, a diferencia del cubo, todos los ángulos en un tetraedro son agudos, lo que le da una apariencia más puntiaguda. Si alguna vez has jugado con un dado de cuatro caras, has estado en contacto con un tetraedro sin siquiera darte cuenta.
El octaedro
El octaedro es otro ejemplo fascinante. Este poliedro tiene ocho caras triangulares y seis vértices. En cada vértice se encuentran cuatro caras, lo que genera ángulos poliedros que son un poco más complejos de visualizar. Este poliedro tiene una simetría que lo hace atractivo en el diseño y en la decoración. Si alguna vez has visto un diseño de joyería que incluye formas geométricas, es posible que hayas visto un octaedro en acción.
La conexión entre los ángulos poliedros y la geometría
Los ángulos poliedros son un aspecto esencial de la geometría tridimensional. Al comprender cómo funcionan y cómo se forman, podemos apreciar mejor el mundo que nos rodea. La geometría no solo se limita a los planos y figuras bidimensionales; es un campo que abarca una variedad de formas y estructuras que existen en nuestro entorno. Desde la arquitectura de edificios hasta la forma en que se organizan los átomos en un cristal, los ángulos poliedros son un componente clave en la comprensión de la geometría en su totalidad.
¿Todos los poliedros tienen ángulos poliedros?
Sí, todos los poliedros tienen ángulos poliedros en sus vértices. Cada vez que se unen tres o más caras en un punto, se forma un ángulo poliedro.
¿Cuántos tipos de ángulos poliedros existen?
Los ángulos poliedros se pueden clasificar de varias maneras, como agudos, rectos y obtusos, dependiendo de su medida. También se pueden clasificar según el número de caras que los rodean.
¿Por qué son importantes los ángulos poliedros en la vida cotidiana?
Los ángulos poliedros son fundamentales en áreas como la arquitectura, la ingeniería y la biología. Comprenderlos ayuda en el diseño de estructuras y en la comprensión de formas naturales.
¿Puedo ver ángulos poliedros en la naturaleza?
Absolutamente. Los ángulos poliedros están presentes en cristales, estructuras biológicas y en la organización de ciertos organismos. La naturaleza está llena de ejemplos de geometría poliedral.
¿Cómo puedo practicar la identificación de ángulos poliedros?
Una buena manera de practicar es observar objetos cotidianos y tratar de identificar sus ángulos poliedros. Puedes comenzar con cubos, tetraedros y otras formas tridimensionales que te rodean.
Este artículo proporciona una visión general sobre los ángulos poliedros, sus propiedades y ejemplos, al tiempo que mantiene un estilo conversacional y accesible. Espero que te sea útil.