¿Alguna vez te has preguntado qué es un poliedro y cómo se relacionan sus ángulos con su forma y estructura? Los poliedros son esas figuras tridimensionales que todos conocemos: cubos, pirámides, dodecaedros y muchos más. Pero más allá de su apariencia, hay un mundo fascinante detrás de los ángulos que componen estas formas. En este artículo, exploraremos todo lo que necesitas saber sobre el ángulo de un poliedro, desde su definición hasta sus propiedades, tipos y algunas curiosidades que te dejarán pensando. Así que, ¡prepárate para sumergirte en el mundo de los poliedros!
¿Qué es un Poliedro?
Antes de adentrarnos en los ángulos, es crucial entender qué es un poliedro. En términos simples, un poliedro es un sólido tridimensional que está formado por caras planas. Estas caras son polígonos y se unen en aristas, que son los segmentos de línea donde se encuentran dos caras. Por ejemplo, imagina un cubo: tiene seis caras cuadradas, doce aristas y ocho vértices. Cada uno de estos elementos juega un papel importante en la estructura del poliedro.
Definición de Ángulo en un Poliedro
Ahora que tenemos una idea clara de lo que es un poliedro, hablemos de los ángulos. En geometría, un ángulo se forma cuando dos líneas se encuentran en un punto. En el contexto de los poliedros, podemos hablar de dos tipos principales de ángulos: los ángulos de las caras y los ángulos sólidos.
Ángulos de las Caras
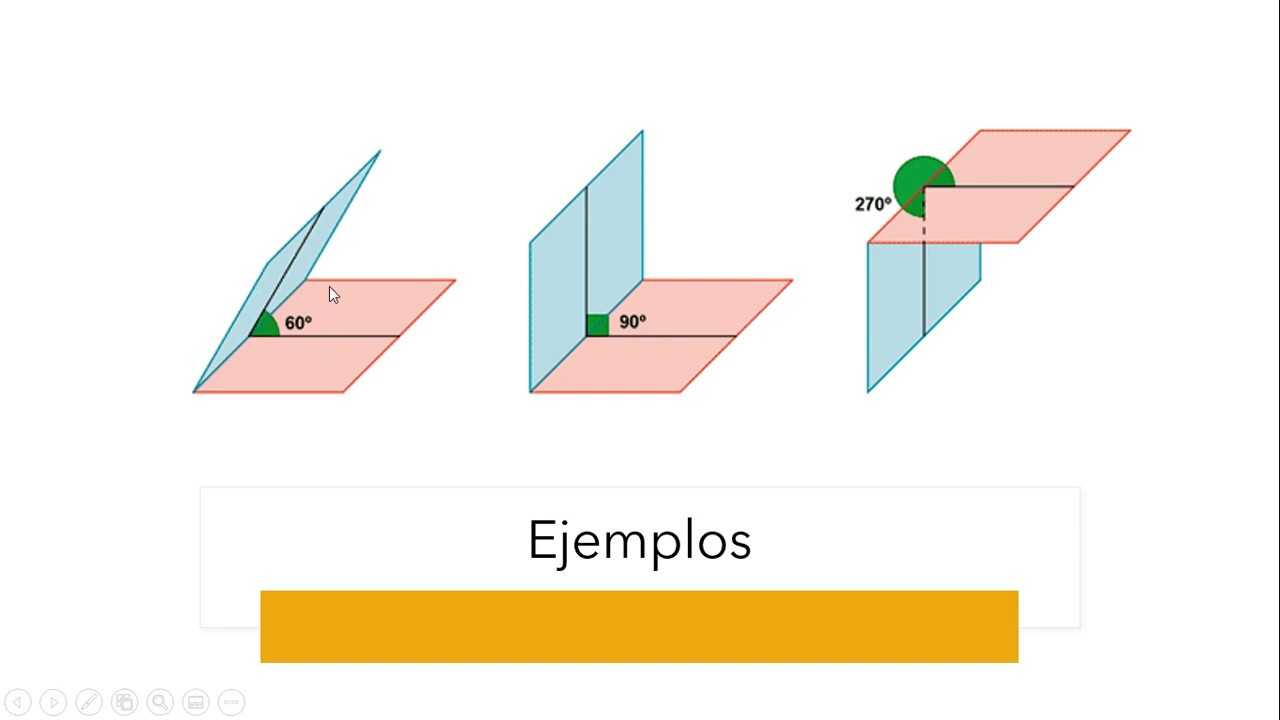
Los ángulos de las caras son simplemente los ángulos que se forman en las intersecciones de las líneas que componen los polígonos que forman cada cara. Por ejemplo, en un cuadrado, todos los ángulos son rectos (90 grados). Pero, ¿qué pasa con un triángulo? Los ángulos en un triángulo pueden variar, lo que afecta la forma de la cara del poliedro.
Ángulos Sólidos
Por otro lado, los ángulos sólidos son un poco más complejos. Se forman en los vértices donde se encuentran varias caras. Piensa en ello como el «ángulo» que se ve desde el vértice hacia las caras que se unen en ese punto. Este tipo de ángulo es esencial para comprender la estructura general del poliedro y cómo se comporta en el espacio tridimensional.
Tipos de Poliedros
Existen varios tipos de poliedros, y cada uno tiene sus propios ángulos y propiedades. Vamos a explorar algunos de los más comunes.
Cubos
El cubo es quizás el poliedro más conocido. Con sus seis caras cuadradas, todos sus ángulos de las caras son de 90 grados. Los ángulos sólidos en cada vértice son la suma de los ángulos de las caras que se encuentran en ese vértice. En el caso del cubo, cada vértice forma un ángulo sólido de 270 grados. ¡Impresionante, ¿verdad?!
Pirámides
Las pirámides son poliedros que tienen una base que puede ser un polígono y caras triangulares que se encuentran en un punto común llamado vértice. Dependiendo de la forma de la base, los ángulos de las caras y los ángulos sólidos pueden variar considerablemente. Por ejemplo, una pirámide cuadrada tiene una base cuadrada y cuatro caras triangulares.
Prismas
Los prismas son poliedros que tienen dos bases paralelas y caras laterales que son paralelogramos. Los ángulos de las caras de un prisma dependen del tipo de polígono que forma las bases. Por ejemplo, un prisma triangular tiene dos bases triangulares y tres caras rectangulares.
Propiedades de los Ángulos en Poliedros
Las propiedades de los ángulos en los poliedros son fascinantes y pueden ser bastante complejas. Una de las propiedades más interesantes es la relación entre el número de caras, vértices y aristas, conocida como la fórmula de Euler.
Fórmula de Euler
La fórmula de Euler establece que para cualquier poliedro convexo, la relación entre el número de vértices (V), aristas (E) y caras (F) es la siguiente:
[ V – E + F = 2 ]
Esta fórmula es increíblemente útil para entender la estructura de los poliedros. Por ejemplo, en un cubo, tenemos 8 vértices, 12 aristas y 6 caras, y si aplicamos la fórmula, obtenemos:
[ 8 – 12 + 6 = 2 ]
¡Funciona a la perfección!
Sumas de Ángulos en las Caras
Otro aspecto interesante es la suma de los ángulos en las caras de un poliedro. Para cualquier polígono, la suma de los ángulos internos se puede calcular usando la fórmula:
[ (n – 2) times 180 ]
donde «n» es el número de lados del polígono. Por ejemplo, en un triángulo (3 lados), la suma de los ángulos es:
[ (3 – 2) times 180 = 180 ]
Esto es fundamental para entender cómo se comportan los ángulos en las diferentes caras de los poliedros.
Aplicaciones de los Poliedros en la Vida Real
Los poliedros no son solo un concepto abstracto en la geometría; tienen aplicaciones prácticas en el mundo real. Desde la arquitectura hasta el diseño de videojuegos, los poliedros son esenciales.
Arquitectura
En arquitectura, los poliedros se utilizan para crear estructuras estéticamente agradables y funcionales. Las formas geométricas complejas pueden dar lugar a edificios innovadores que son tanto visualmente atractivos como estructuralmente sólidos.
Diseño Gráfico y Videojuegos
En el mundo digital, los poliedros son fundamentales en el diseño gráfico y la creación de videojuegos. Los modelos 3D que vemos en los videojuegos a menudo se construyen utilizando poliedros, lo que permite crear entornos ricos y detallados.
Curiosidades sobre Poliedros y sus Ángulos
A medida que exploramos más sobre los poliedros, encontramos algunas curiosidades que pueden sorprenderte.
Poliedros Regulares
¿Sabías que hay solo cinco poliedros regulares convexos? Estos son conocidos como los sólidos de Platón: el tetraedro, cubo, octaedro, dodecaedro y icosaedro. Cada uno tiene caras que son polígonos regulares y ángulos sólidos que son idénticos en cada vértice.
El Papel de los Poliedros en la Naturaleza
Los poliedros también pueden encontrarse en la naturaleza. Por ejemplo, los cristales de sal a menudo forman estructuras cúbicas, y los panales de las abejas tienen una forma hexagonal que maximiza el espacio y minimiza el material utilizado. ¡La naturaleza es una gran arquitecta!
¿Cuál es la diferencia entre un poliedro convexo y uno cóncavo?
Un poliedro convexo tiene todos sus ángulos sólidos que son menores de 360 grados, mientras que un poliedro cóncavo tiene al menos un ángulo sólido mayor de 360 grados. Esto significa que en un poliedro cóncavo, puedes «ver» hacia adentro de la figura.
¿Cómo se pueden calcular los ángulos sólidos en un poliedro?
Los ángulos sólidos se pueden calcular usando la suma de los ángulos de las caras que se encuentran en el vértice. Para un poliedro regular, todos los ángulos sólidos son iguales, lo que facilita su cálculo.
¿Por qué son importantes los poliedros en matemáticas?
Los poliedros son fundamentales en matemáticas porque nos ayudan a entender conceptos de geometría tridimensional, y su estudio puede llevar a descubrimientos en diversas áreas, como la topología y la teoría de grafos.
¿Se pueden encontrar poliedros en el arte?
¡Absolutamente! Muchos artistas han utilizado poliedros en sus obras, y las estructuras de arte moderno a menudo incorporan formas geométricas complejas que recuerdan a los poliedros.
¿Cómo se relacionan los poliedros con el espacio tridimensional?
Los poliedros son una forma de representar objetos en el espacio tridimensional. Cada poliedro tiene una estructura única que define cómo se relaciona con el espacio, lo que es esencial en campos como la arquitectura, la ingeniería y la animación 3D.
En resumen, los ángulos de los poliedros son una parte fundamental de su estructura y comprensión. Desde sus definiciones hasta sus aplicaciones en la vida real, hay mucho que aprender sobre estos fascinantes sólidos. ¡Así que la próxima vez que veas un cubo o una pirámide, recuerda que hay mucho más detrás de su forma!