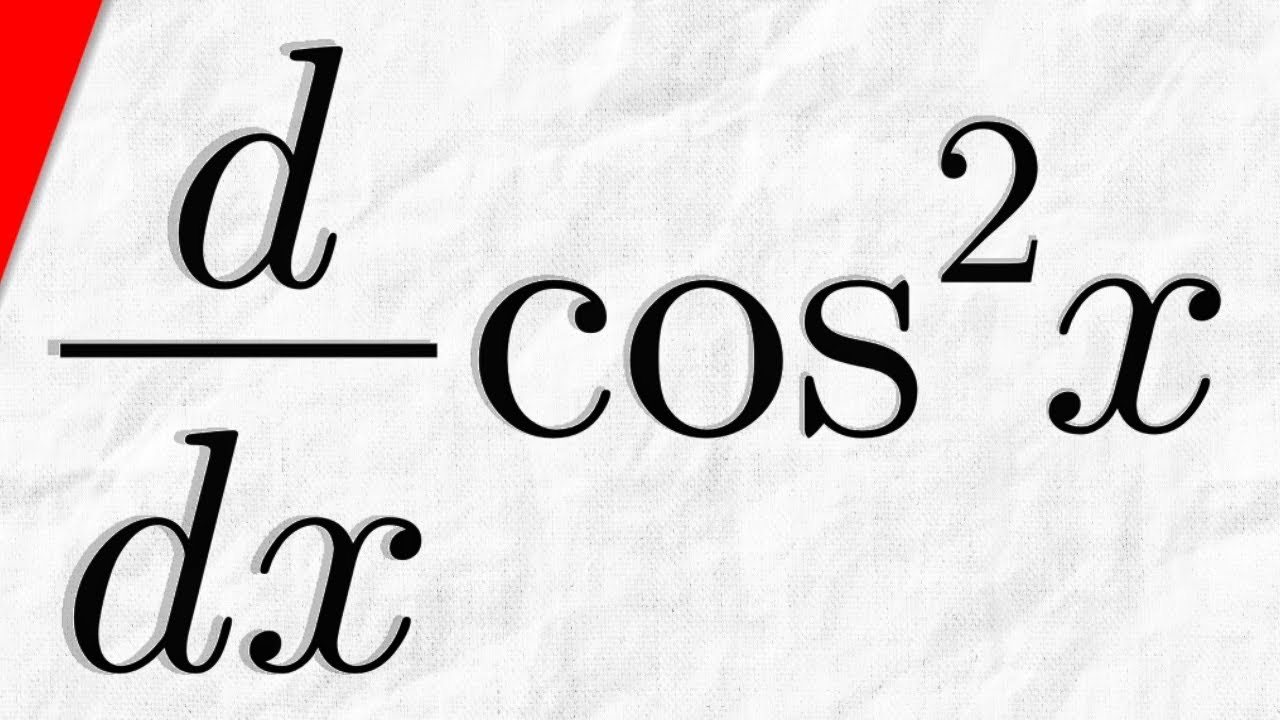¿Alguna vez te has preguntado cómo se calcula la derivada de funciones trigonométricas? Si es así, ¡estás en el lugar correcto! Hoy vamos a desglosar el proceso de calcular la derivada de cos(2x) de una manera sencilla y comprensible. La derivada es una herramienta fundamental en cálculo que nos ayuda a entender cómo cambian las funciones en relación con sus variables. En este caso, nos centraremos en la función coseno y su transformación cuando se multiplica por un número. Así que, si estás listo para sumergirte en el mundo de las derivadas, ¡comencemos!
## ¿Qué es una Derivada?
Para empezar, vamos a desmenuzar el concepto de derivada. En términos simples, la derivada de una función en un punto nos dice la pendiente de la tangente a la curva de esa función en ese punto. Imagina que estás conduciendo un coche en una carretera montañosa. La pendiente de la carretera en un punto específico es como la derivada: te dice si estás subiendo o bajando, y qué tan empinada es la subida o la bajada.
En matemáticas, la derivada se denota comúnmente como f'(x) o dy/dx. Y cuando hablamos de funciones trigonométricas, como coseno, el proceso puede parecer un poco complicado, pero con práctica, se vuelve más fácil. Vamos a ver cómo se aplica esto específicamente a la función cos(2x).
## La Regla de la Cadena: Tu Mejor Amiga
Cuando trabajamos con funciones compuestas, como cos(2x), la regla de la cadena es esencial. Esta regla nos dice que si tienes una función dentro de otra, debes derivar la función exterior y luego multiplicarla por la derivada de la función interior. Para la función cos(2x), la función exterior es el coseno y la función interior es 2x.
### Paso 1: Derivar la Función Exterior
La derivada del coseno es -sen(x). Pero como nuestra función es cos(2x), debemos aplicar la regla de la cadena. Así que la derivada de la función exterior, que es cos(u) donde u = 2x, se convierte en:
[
frac{d}{dx} [cos(2x)] = -sen(2x)
]
### Paso 2: Derivar la Función Interior
Ahora, pasamos a la función interior, que es 2x. La derivada de 2x es simplemente 2. Ahora, aplicamos la regla de la cadena:
[
frac{d}{dx} [cos(2x)] = -sen(2x) cdot 2
]
### Paso 3: Combinar los Resultados
Finalmente, combinamos todo. La derivada de cos(2x) es:
[
frac{d}{dx} [cos(2x)] = -2sen(2x)
]
Y ahí lo tienes, la derivada de cos(2x) es -2sen(2x). ¡Sencillo, verdad? Pero no te vayas todavía, porque hay mucho más que podemos explorar.
## Aplicaciones de la Derivada de cos(2x)
Ahora que sabes cómo calcular la derivada de cos(2x), es importante entender por qué esto es útil. Las derivadas tienen aplicaciones en diversas áreas como la física, la ingeniería y la economía. Por ejemplo, si estás analizando el movimiento de un objeto en un plano, la derivada te puede ayudar a encontrar la velocidad instantánea en un momento dado.
### Ejemplo en Física
Imagina que estás lanzando una pelota hacia arriba. La altura de la pelota en función del tiempo podría describirse con una función que involucra cosenos. Al calcular la derivada, podrías determinar la velocidad de la pelota en cualquier instante. Esto es crucial para entender el movimiento y predecir el comportamiento del objeto.
## Ejercicios Prácticos
Ahora que hemos cubierto el cálculo de la derivada, ¿qué tal si lo intentamos con algunos ejercicios prácticos? Aquí tienes algunos ejemplos para practicar.
### Ejercicio 1
Calcula la derivada de la función f(x) = cos(3x).
Solución:
1. Derivada de cos(u) es -sen(u).
2. La función interior es 3x, cuya derivada es 3.
3. Aplicando la regla de la cadena:
[
f'(x) = -sen(3x) cdot 3 = -3sen(3x)
]
### Ejercicio 2
Ahora intenta calcular la derivada de g(x) = cos(4x + 1).
Solución:
1. Derivada de cos(u) es -sen(u).
2. La función interior es 4x + 1, cuya derivada es 4.
3. Aplicando la regla de la cadena:
[
g'(x) = -sen(4x + 1) cdot 4 = -4sen(4x + 1)
]
## Errores Comunes al Calcular Derivadas
Aunque calcular derivadas puede ser sencillo, hay algunos errores comunes que los estudiantes suelen cometer. Aquí te dejo algunos para que los evites.
### Confundir las Funciones
Es fácil confundirse al derivar funciones compuestas. Asegúrate de identificar correctamente cuál es la función exterior y cuál es la interior. Recuerda, la regla de la cadena es tu aliada.
### Olvidar la Derivada de la Función Interior
No olvides multiplicar por la derivada de la función interior. Este es un paso crucial en la aplicación de la regla de la cadena.
### No Simplificar la Respuesta
A veces, después de calcular la derivada, se puede simplificar. Asegúrate de presentar tu respuesta en la forma más simple posible.
## Conclusión
Calcular la derivada de cos(2x) puede parecer complicado al principio, pero con práctica y comprensión de la regla de la cadena, se convierte en una tarea mucho más manejable. Recuerda que las derivadas son una herramienta poderosa que te ayudará a entender el comportamiento de las funciones en muchas disciplinas.
### Preguntas Frecuentes
1. ¿Por qué es importante la derivada en matemáticas?
La derivada nos ayuda a entender cómo cambian las funciones, lo que es crucial en muchas aplicaciones prácticas.
2. ¿Qué otras funciones trigonométricas puedo derivar?
Puedes derivar funciones como sen(x), tan(x), y muchas más usando reglas similares.
3. ¿Existen otros métodos para calcular derivadas?
Sí, además de la regla de la cadena, hay métodos como la regla del producto y la regla del cociente.
4. ¿Qué pasa si la función es más complicada?
Si la función tiene más términos o es más compleja, sigue aplicando las reglas de derivación paso a paso.
5. ¿Puedo calcular derivadas sin saber límites?
Aunque entender límites es útil, puedes aprender a derivar utilizando las reglas de derivación sin entrar en los detalles de los límites.
Espero que esta guía te haya sido útil y que ahora te sientas más cómodo calculando derivadas. ¡Sigue practicando y no dudes en hacer preguntas si te surgen dudas!