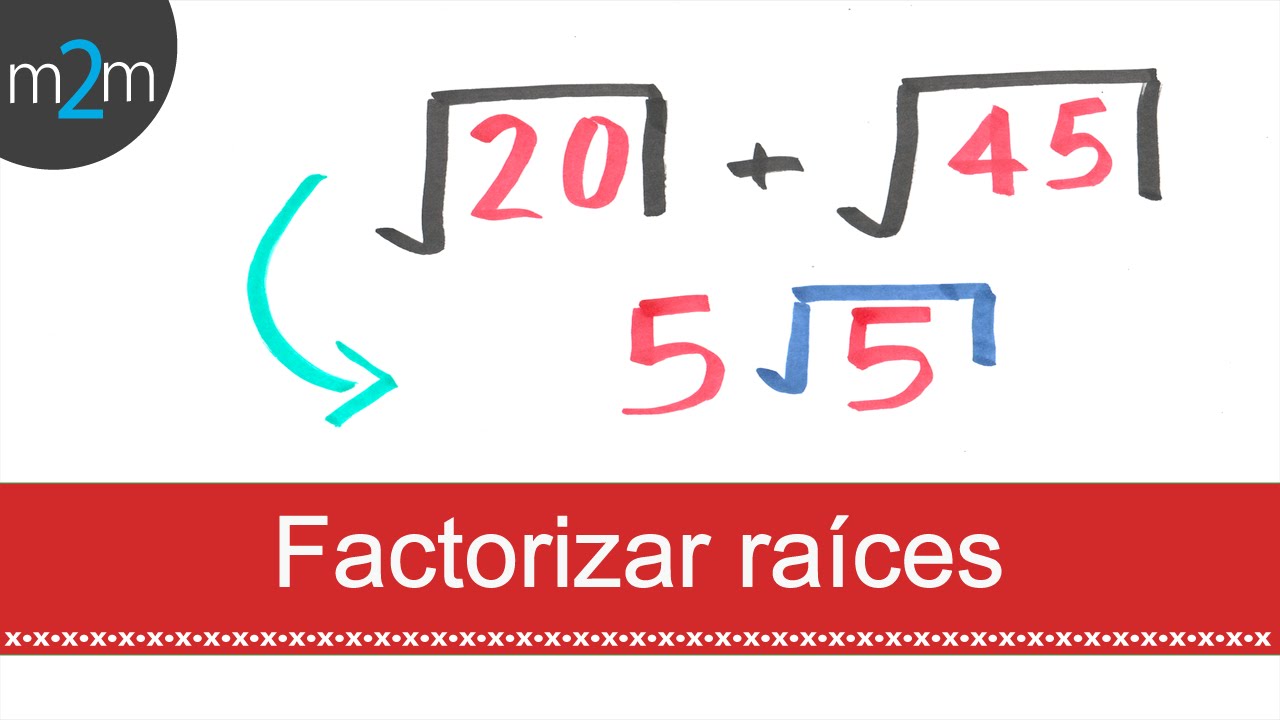
¡Hola! Si has llegado hasta aquí, es probable que estés buscando entender un tema que puede parecer complicado al principio, pero que en realidad es muy fascinante: la factorización de raíces. ¿Te suena familiar? Si no, no te preocupes, porque en esta guía completa desglosaremos este concepto de manera sencilla y práctica. La factorización es una herramienta esencial en matemáticas, especialmente cuando se trata de polinomios y ecuaciones cuadráticas. Pero, ¿qué es exactamente la factorización de raíces y por qué deberías preocuparte por ella? Vamos a descubrirlo juntos.
¿Qué es la Factorización de Raíces?
En términos simples, la factorización de raíces implica descomponer una expresión algebraica en sus factores más simples. Imagina que tienes un rompecabezas; la factorización es como separar las piezas para que puedas entender mejor cómo encajan. En el caso de polinomios, estamos buscando raíces o soluciones de ecuaciones, y la factorización nos ayuda a encontrarlas de manera más eficiente.
La Importancia de la Factorización de Raíces
La factorización no es solo un ejercicio académico; tiene aplicaciones prácticas en el mundo real. Desde resolver problemas de ingeniería hasta optimizar funciones en economía, la capacidad de factorizar ecuaciones puede ser extremadamente útil. ¿Alguna vez has intentado optimizar algo, como el espacio en tu habitación o tu tiempo durante el día? La factorización es una forma de optimizar las soluciones a problemas matemáticos.
Los Métodos de Factorización
Ahora que tenemos una idea general de qué es la factorización de raíces, vamos a explorar algunos de los métodos más comunes que puedes utilizar. No te preocupes, no es tan complicado como parece. Vamos a desglosarlo paso a paso.
Factorización por Agrupación
Este método es bastante útil cuando tienes cuatro términos o más en tu polinomio. La idea es agrupar los términos en pares y luego factorizar cada par. Por ejemplo, considera la expresión:
x^3 + 3x^2 + 2x + 6
Puedes agruparla así:
(x^3 + 3x^2) + (2x + 6)
Ahora, factoriza cada grupo:
x^2(x + 3) + 2(x + 3)
Finalmente, puedes sacar el factor común:
(x + 3)(x^2 + 2)
Factorización por Diferencia de Cuadrados
Este método se aplica cuando tienes una expresión que puede ser escrita como la diferencia de dos cuadrados. La fórmula básica es:
a^2 - b^2 = (a + b)(a - b)
Por ejemplo:
x^2 - 16
Esto se puede escribir como:
(x + 4)(x - 4)
¡Sencillo, verdad? La clave aquí es identificar los cuadrados perfectos.
Factorización de Trinomios
Los trinomios son expresiones con tres términos. La forma más común es ax^2 + bx + c. Para factorizar, buscamos dos números que multiplicados den ac y sumados den b. Por ejemplo, en el trinomio:
x^2 + 5x + 6
Buscamos dos números que multiplicados den 6 y sumados den 5. Estos números son 2 y 3. Por lo tanto, podemos factorizarlo como:
(x + 2)(x + 3)
Ejemplos Prácticos de Factorización
Ahora que hemos cubierto algunos métodos, veamos algunos ejemplos prácticos para que puedas ver cómo se aplica todo esto en la vida real.
Ejemplo 1: Factorización de un Polinomio Complejo
Supongamos que tienes el polinomio:
2x^3 + 4x^2 - 2x - 4
Primero, podemos agrupar:
(2x^3 + 4x^2) + (-2x - 4)
Ahora, factorizamos cada grupo:
2x^2(x + 2) - 2(x + 2)
Extraemos el factor común:
(x + 2)(2x^2 - 2)
Y simplificamos:
(x + 2)(2(x^2 - 1))
Finalmente, aplicamos la diferencia de cuadrados:
(x + 2)(2(x + 1)(x - 1))
Ejemplo 2: Resolviendo una Ecuación Cuadrática
Imagina que tienes la ecuación cuadrática:
x^2 - 5x + 6 = 0
Podemos factorizarla utilizando el método de trinomios. Buscamos dos números que multiplicados den 6 y sumados den -5, que son -2 y -3. Por lo tanto:
(x - 2)(x - 3) = 0
Esto nos da las soluciones:
x = 2 y x = 3.
Consejos para Mejorar en la Factorización
Si bien la factorización puede parecer desafiante al principio, hay algunos consejos que pueden ayudarte a mejorar. ¿Estás listo para algunos trucos?
- Practica regularmente: La práctica hace al maestro. Cuanto más practiques, más cómodo te sentirás.
- Usa recursos en línea: Hay muchos videos y tutoriales que pueden ayudarte a entender los conceptos de manera visual.
- Forma grupos de estudio: A veces, explicar un concepto a alguien más puede ayudarte a entenderlo mejor.
¿Por qué es importante la factorización en matemáticas?
La factorización es crucial porque simplifica la resolución de ecuaciones y permite entender mejor las propiedades de los polinomios. Además, tiene aplicaciones en diversas áreas como la física y la economía.
¿Puedo factorizar cualquier polinomio?
No todos los polinomios son factorizables en números reales. Sin embargo, muchos polinomios pueden ser factorizados utilizando métodos adecuados, y algunos pueden requerir números complejos.
¿Qué hago si no puedo factorizar un polinomio?
Si te encuentras con un polinomio que parece no ser factorizable, puedes intentar métodos alternativos, como la fórmula cuadrática o la aproximación numérica.
¿La factorización se aplica solo a polinomios?
No, aunque la factorización es más comúnmente asociada con polinomios, también se puede aplicar a otros tipos de expresiones algebraicas, como fracciones y raíces.
Así que ahí lo tienes. La factorización de raíces no es solo un tema más en tu lista de tareas, sino una herramienta poderosa que te ayudará en tu viaje matemático. ¡Espero que esta guía te haya sido útil y que ahora te sientas más seguro al abordar problemas de factorización! ¿Listo para ponerlo en práctica?