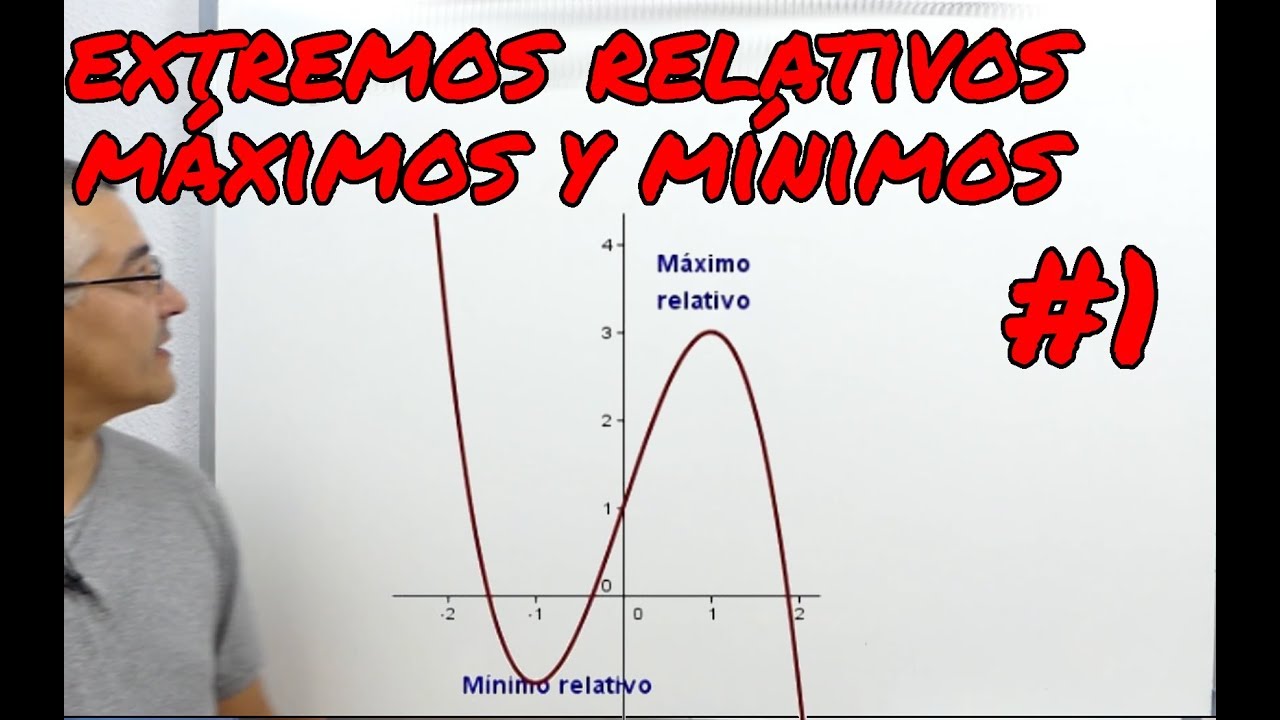
¿Alguna vez te has preguntado qué hace que una montaña sea más alta que otra? O, en términos más matemáticos, ¿cómo podemos identificar los puntos más altos y más bajos de una función? Esto es precisamente lo que se conoce como extremos relativos. En este artículo, vamos a sumergirnos en el fascinante mundo de los extremos relativos de una función, explorando su significado, su importancia y cómo podemos identificarlos. Así que, si estás listo, ¡vamos a desglosar este concepto!
Los extremos relativos son esos puntos en una función donde esta alcanza un valor máximo o mínimo local. Imagina que estás en un paseo por un terreno montañoso; en algunos puntos, podrías estar en la cima de una colina (un máximo relativo) o en el fondo de un valle (un mínimo relativo). Pero, ¿por qué son importantes estos puntos? Bueno, no solo son útiles para entender el comportamiento de las funciones, sino que también tienen aplicaciones prácticas en áreas como la economía, la biología y la ingeniería. ¡Así que no subestimes su valor!
¿Qué son los Extremos Relativos?
Para entender a fondo qué son los extremos relativos, primero debemos definir algunos términos clave. Un extremo relativo se refiere a un punto en el que la función cambia de dirección. Es decir, un máximo relativo es un punto donde la función alcanza un valor más alto que en los puntos cercanos, mientras que un mínimo relativo es donde la función tiene un valor más bajo.
Pero, ¿cómo sabemos cuándo estamos en uno de estos puntos? Aquí es donde entran en juego las derivadas. La primera derivada de una función nos dice la pendiente de la misma en un punto dado. Si la derivada cambia de positiva a negativa, estamos en un máximo relativo. Por otro lado, si la derivada cambia de negativa a positiva, hemos encontrado un mínimo relativo. ¡Es como tener un mapa que nos guía a través del terreno montañoso!
La Importancia de los Extremos Relativos
¿Por qué deberíamos preocuparnos por los extremos relativos? La respuesta es sencilla: nos ayudan a entender el comportamiento de una función. En el mundo real, muchas situaciones pueden modelarse con funciones matemáticas. Por ejemplo, en economía, los extremos relativos pueden indicar el punto de máxima ganancia o pérdida. En biología, pueden representar el crecimiento máximo de una población. Sin duda, entender estos puntos puede ser clave para tomar decisiones informadas.
Además, los extremos relativos son esenciales en el cálculo de optimización. Imagina que eres un ingeniero que necesita diseñar una estructura. Comprender dónde se encuentran los máximos y mínimos puede ayudar a asegurar que la estructura sea segura y eficiente. Así que, como puedes ver, los extremos relativos son más que solo puntos en un gráfico; son herramientas poderosas en la toma de decisiones.
Cómo Encontrar Extremos Relativos
Ahora que entendemos qué son y por qué son importantes, vamos a ver cómo podemos encontrarlos. A continuación, te presento un método paso a paso para identificar extremos relativos en una función.
Paso 1: Encuentra la Derivada
El primer paso es encontrar la primera derivada de la función. Esto implica utilizar las reglas de derivación que ya conoces. Por ejemplo, si tienes la función ( f(x) = x^2 – 4x + 4 ), la derivada sería ( f'(x) = 2x – 4 ).
Paso 2: Igualar a Cero
Una vez que tengas la derivada, el siguiente paso es igualarla a cero para encontrar los puntos críticos. Esto se debe a que los extremos relativos se encuentran donde la pendiente de la función es cero. En nuestro ejemplo, igualamos ( 2x – 4 = 0 ) y encontramos que ( x = 2 ).
Paso 3: Prueba de la Segunda Derivada
Ahora que tenemos los puntos críticos, necesitamos determinar si son máximos o mínimos relativos. Aquí es donde entra la segunda derivada. Si la segunda derivada es positiva en el punto crítico, entonces es un mínimo relativo. Si es negativa, es un máximo relativo. En nuestro caso, la segunda derivada de ( f(x) ) sería ( f»(x) = 2 ), que es positiva. Por lo tanto, ( x = 2 ) es un mínimo relativo.
Ejemplos Prácticos
Veamos un par de ejemplos prácticos para reforzar lo que hemos aprendido.
Ejemplo 1: Función Cuadrática
Consideremos la función ( f(x) = -x^2 + 4x ). Primero, encontramos la derivada: ( f'(x) = -2x + 4 ). Igualamos a cero: ( -2x + 4 = 0 ), lo que nos da ( x = 2 ). Ahora, calculamos la segunda derivada: ( f»(x) = -2 ), que es negativa. Por lo tanto, ( x = 2 ) es un máximo relativo. Si graficamos esta función, veremos que efectivamente alcanza un punto alto en ( x = 2 ).
Ejemplo 2: Función Trigonométrica
Tomemos la función ( f(x) = sin(x) ). La derivada es ( f'(x) = cos(x) ). Para encontrar los extremos relativos, igualamos a cero: ( cos(x) = 0 ). Esto sucede en ( x = frac{pi}{2} + kpi ) para cualquier entero ( k ). La segunda derivada ( f»(x) = -sin(x) ) nos dirá si son máximos o mínimos. Así que, dependiendo del valor de ( k ), podemos identificar los extremos.
Aplicaciones de los Extremos Relativos
Como mencionamos anteriormente, los extremos relativos tienen múltiples aplicaciones en la vida real. Vamos a explorar algunas de ellas.
Optimización en Negocios
En el mundo de los negocios, las empresas buscan maximizar sus beneficios o minimizar sus costos. Aquí es donde los extremos relativos son esenciales. Utilizando cálculos para encontrar estos puntos, las empresas pueden determinar la cantidad óptima de productos a producir o el precio ideal para maximizar las ganancias.
Estudio de Fenómenos Naturales
En biología, los científicos utilizan extremos relativos para estudiar el crecimiento de poblaciones. Por ejemplo, al analizar la función que representa el crecimiento de una especie, pueden identificar los puntos donde la población alcanza su máximo o mínimo, lo que puede ayudar a prever cambios en el ecosistema.
¿Los extremos relativos siempre son máximos o mínimos absolutos?
No necesariamente. Los extremos relativos son puntos donde la función alcanza un máximo o mínimo en un rango limitado, mientras que los máximos y mínimos absolutos son los valores más altos o bajos en todo el dominio de la función.
¿Qué sucede si la derivada no se anula?
Si la derivada nunca se anula, entonces la función no tiene extremos relativos. Esto puede suceder en funciones que son estrictamente crecientes o decrecientes.
¿Cómo afecta la forma de la función a los extremos relativos?
La forma de la función puede influir en la cantidad y ubicación de los extremos relativos. Por ejemplo, funciones polinómicas de grado mayor pueden tener más puntos críticos que funciones lineales.
¿Es posible que una función no tenga extremos relativos?
Sí, hay funciones que no tienen extremos relativos. Un ejemplo clásico es la función exponencial ( f(x) = e^x ), que siempre es creciente.
¿Los extremos relativos son útiles en todas las disciplinas?
Definitivamente. Desde la economía hasta la ingeniería, los extremos relativos son herramientas valiosas para optimizar y entender comportamientos en diversas disciplinas.
En resumen, los extremos relativos son fundamentales para entender el comportamiento de las funciones y tienen aplicaciones prácticas en muchos campos. Ahora que tienes un conocimiento más profundo sobre ellos, ¡es hora de poner en práctica lo que has aprendido! ¿Te animas a buscar extremos relativos en tus funciones favoritas?