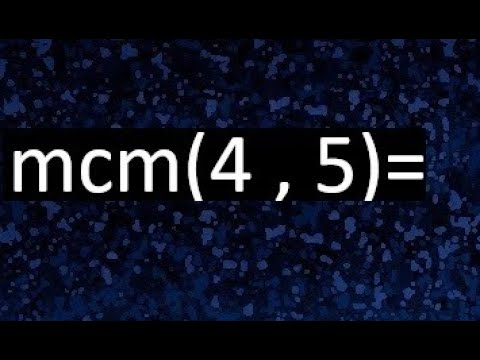¿Qué es el Mínimo Común Múltiplo y por qué es importante?
¡Hola! Hoy vamos a sumergirnos en el fascinante mundo de los números, específicamente en el concepto del Mínimo Común Múltiplo (MCM). Tal vez te estés preguntando, ¿qué es eso y por qué debería importarme? Bueno, el MCM es como el mejor amigo de los números cuando se trata de resolver problemas matemáticos. Es la manera de encontrar un número que es múltiplo de dos o más números, y que además es el más pequeño posible. Imagina que tienes un par de amigos que siempre se encuentran a la misma hora, pero en días diferentes. El MCM te dice cuándo será la próxima vez que coincidan. ¿No es genial?
Para entenderlo mejor, tomemos como ejemplo los números 4 y 5. Si alguna vez has tenido que sincronizar actividades o eventos, sabes lo crucial que es encontrar ese punto en común. Así que, acompáñame en este recorrido donde desglosaremos el MCM de 4 y 5 de una manera sencilla y amigable. ¡Vamos a ello!
¿Cómo se calcula el Mínimo Común Múltiplo?
Calcular el MCM puede parecer complicado al principio, pero una vez que entiendes el proceso, verás que es pan comido. Hay varios métodos para encontrarlo, pero aquí nos centraremos en dos de los más comunes: el método de los múltiplos y el método de la descomposición en factores primos. ¡Empecemos!
Método de los múltiplos
Primero, echemos un vistazo al método de los múltiplos. Para encontrar el MCM de 4 y 5, comenzamos listando los múltiplos de cada número:
- Múltiplos de 4: 4, 8, 12, 16, 20, 24, 28, 32, …
- Múltiplos de 5: 5, 10, 15, 20, 25, 30, …
Ahora, busquemos el primer número que aparece en ambas listas. Si observas, el número 20 es el primer múltiplo que se repite. Por lo tanto, el MCM de 4 y 5 es 20. ¡Así de fácil!
Método de la descomposición en factores primos
Si prefieres un enfoque más matemático, podemos utilizar la descomposición en factores primos. Para esto, primero descomponemos cada número en sus factores primos:
- 4 = 2 × 2 (o 2²)
- 5 = 5 (que es primo)
Luego, tomamos cada factor primo, elevándolo a la mayor potencia que aparece en la descomposición. En este caso, tenemos:
- 2² (de 4)
- 5¹ (de 5)
Ahora, multiplicamos estos factores: 2² × 5¹ = 4 × 5 = 20. Y voilà, hemos encontrado el MCM de 4 y 5 nuevamente, ¡que es 20!
Aplicaciones del Mínimo Común Múltiplo
Una vez que has aprendido a calcular el MCM, es hora de hablar sobre por qué es tan útil. El MCM se utiliza en diversas situaciones, desde la resolución de problemas de fracciones hasta la planificación de eventos. Pero vamos a ver algunos ejemplos concretos.
Problemas de fracciones
Imagina que estás tratando de sumar dos fracciones, digamos 1/4 y 1/5. Para sumarlas, necesitas un denominador común. Aquí es donde el MCM entra en juego. Como ya sabemos que el MCM de 4 y 5 es 20, puedes convertir ambas fracciones:
- 1/4 = 5/20
- 1/5 = 4/20
Así que ahora puedes sumarlas fácilmente: 5/20 + 4/20 = 9/20. ¡Sencillo, verdad?
Planificación de eventos
Imagina que tienes dos eventos: uno ocurre cada 4 días y otro cada 5 días. Si quieres saber cuándo ambos eventos sucederán al mismo tiempo, necesitas encontrar el MCM. Ya sabemos que el MCM de 4 y 5 es 20, así que ambos eventos coincidirán cada 20 días. Esto puede ser muy útil si estás organizando actividades o eventos y necesitas sincronizar horarios.
¿Por qué es útil conocer el MCM?
El MCM no solo es útil en matemáticas, sino que también tiene aplicaciones prácticas en la vida diaria. Aquí hay algunas razones por las que deberías considerar aprender a calcularlo:
- Resolución de problemas: Como mencionamos, el MCM es fundamental para resolver problemas de fracciones y para encontrar denominadores comunes.
- Planificación: Facilita la organización de eventos, permitiéndote saber cuándo se cruzarán diferentes actividades.
- Fundamentos matemáticos: Entender el MCM te ayuda a construir una base sólida en matemáticas, lo cual es esencial para aprender conceptos más avanzados.
Ejercicios prácticos para dominar el MCM
Ahora que has aprendido a calcular el MCM y su importancia, es momento de ponerlo en práctica. Aquí te dejo algunos ejercicios que puedes intentar por tu cuenta:
Ejercicio 1
Encuentra el MCM de 6 y 8. ¿Puedes hacerlo usando ambos métodos? ¡Inténtalo!
Ejercicio 2
Ahora, intenta calcular el MCM de 3, 7 y 9. Este es un poco más complicado, pero estoy seguro de que puedes hacerlo.
Ejercicio 3
¿Qué tal si ahora encuentras el MCM de 10 y 15? Recuerda, puedes usar la lista de múltiplos o la descomposición en factores primos. ¡Vamos, tú puedes!
¿El MCM siempre es mayor que los números originales?
No necesariamente. En algunos casos, el MCM puede ser igual a uno de los números si uno es múltiplo del otro. Por ejemplo, el MCM de 5 y 10 es 10.
¿El MCM se puede utilizar con números negativos?
El MCM generalmente se calcula solo con números positivos. Sin embargo, si consideras los valores absolutos de los números negativos, puedes encontrar el MCM de la misma manera.
¿El MCM es lo mismo que el Máximo Común Divisor (MCD)?
No, el MCM y el MCD son conceptos diferentes. El MCM es el múltiplo común más pequeño, mientras que el MCD es el divisor común más grande de dos o más números.
¿Se puede calcular el MCM de más de dos números?
¡Sí! Puedes calcular el MCM de tres o más números utilizando los mismos métodos. Simplemente encuentra el MCM de dos números y luego usa ese resultado para calcular el MCM con el siguiente número.
¿Dónde puedo practicar más sobre el MCM?
Hay muchos recursos en línea, desde aplicaciones educativas hasta sitios web interactivos donde puedes practicar problemas de MCM. ¡No dudes en explorar!
Así que ahí lo tienes, una guía completa sobre el Mínimo Común Múltiplo de 4 y 5. Espero que ahora te sientas más cómodo con este concepto y que puedas aplicarlo en tu vida diaria. ¡No dudes en practicar y preguntar si tienes más dudas!