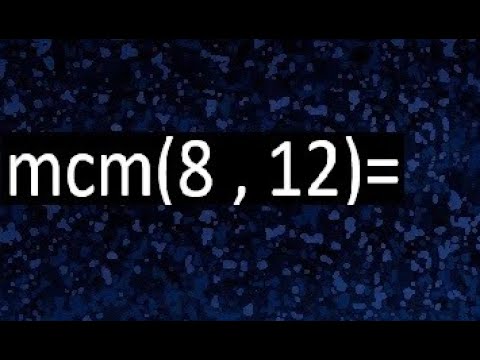Entendiendo el MCM: Un Concepto Clave en Matemáticas
¡Hola, amigo lector! Si alguna vez te has preguntado qué es eso del MCM y por qué es tan importante, estás en el lugar correcto. Hoy vamos a desglosar el concepto de Mínimo Común Múltiplo (MCM) de los números 8 y 12. Pero antes de lanzarnos a los números, imaginemos que estamos organizando una fiesta. ¿Te imaginas? Tienes dos tipos de globos, uno de color azul y otro de color rojo. Los globos azules vienen en paquetes de 8 y los rojos en paquetes de 12. Si quieres que todos los globos estén bien organizados y que no sobre ninguno, necesitas saber cuántos paquetes de cada uno debes comprar. Ahí es donde entra el MCM, porque te ayuda a encontrar la cantidad mínima de globos que puedes comprar sin que sobren. Así que, ¡pongámonos manos a la obra!
¿Qué es el MCM y por qué es útil?
El Mínimo Común Múltiplo es, como su nombre indica, el menor múltiplo que comparten dos o más números. En nuestro caso, queremos encontrar el MCM de 8 y 12. Pero, ¿por qué es útil conocerlo? Bueno, en matemáticas y en la vida diaria, muchas veces necesitamos encontrar un número que sea común entre varias cantidades. Esto puede ser útil en situaciones de programación, planificación de eventos, y hasta en la cocina, cuando estamos ajustando recetas. Imagina que estás haciendo una pizza y necesitas dividir los ingredientes en porciones. El MCM te puede ayudar a asegurarte de que no te falte ni un solo ingrediente. ¡Interesante, ¿verdad?
¿Cómo calcular el MCM de 8 y 12?
Ahora que sabemos qué es el MCM, vamos a descubrir cómo calcularlo. Hay varios métodos para hacerlo, pero aquí te explicaré dos de los más comunes: el método de la lista de múltiplos y el método de la descomposición en factores primos. Así que, sin más preámbulos, ¡vamos a ello!
Método 1: Lista de Múltiplos
Este es el método más sencillo y, a menudo, el más visual. Todo lo que tienes que hacer es listar los múltiplos de cada número hasta que encuentres el primero que sea común. Para el número 8, los primeros múltiplos son:
- 8
- 16
- 24
- 32
- 40
Y para el número 12, los múltiplos son:
- 12
- 24
- 36
- 48
Al observar las listas, vemos que el primer múltiplo que ambos números comparten es el 24. ¡Así que el MCM de 8 y 12 es 24!
Método 2: Descomposición en Factores Primos
Este método puede parecer un poco más complicado, pero en realidad es bastante fácil una vez que lo entiendes. Primero, descomponemos cada número en sus factores primos. Para el 8, tenemos:
- 8 = 2 × 2 × 2 = 2³
Y para el 12, la descomposición es:
- 12 = 2 × 2 × 3 = 2² × 3
Ahora, para encontrar el MCM, tomamos cada factor primo y usamos el exponente más alto que aparece en cualquiera de las descomposiciones. En nuestro caso, los factores son 2 y 3. Así que tomamos:
- Para el 2: el mayor exponente es 3 (de 8).
- Para el 3: el mayor exponente es 1 (de 12).
Multiplicamos estos factores juntos: 2³ × 3¹ = 8 × 3 = 24. Y, ¡voilà! Nuevamente, el MCM de 8 y 12 es 24.
Aplicaciones del MCM en la Vida Real
Ahora que hemos encontrado el MCM, quizás te estés preguntando: «¿Y ahora qué?» Bueno, el MCM tiene muchas aplicaciones prácticas en nuestra vida diaria. Aquí te presento algunas situaciones donde puede ser muy útil:
Organización de Eventos
Imagina que estás organizando un evento y necesitas coordinar actividades que se repiten en intervalos diferentes. Si tienes actividades que ocurren cada 8 y 12 minutos, el MCM te ayudará a saber cada cuántos minutos se alinearán ambas actividades. Así podrás planificar mejor el evento y asegurarte de que todo fluya sin problemas.
Recetas de Cocina
Si te gusta cocinar, seguro que has ajustado recetas para más o menos porciones. Supongamos que una receta sirve para 8 personas y otra para 12. Si quieres hacer una comida para 24 personas, el MCM te ayudará a determinar las cantidades correctas de cada ingrediente para que no te falte nada y no sobre demasiado.
Rutas de Transporte
En el mundo del transporte, especialmente en horarios de autobuses o trenes, el MCM puede ser útil. Si un autobús sale cada 8 minutos y otro cada 12, el MCM te dirá cada cuánto tiempo ambos autobuses estarán en la estación al mismo tiempo. Esto puede ser útil para planificar tu viaje y evitar largas esperas.
¿El MCM siempre es mayor que los números originales?
No necesariamente. En algunos casos, el MCM puede ser igual a uno de los números si uno es múltiplo del otro. Por ejemplo, el MCM de 5 y 10 es 10.
¿Qué pasa si no hay múltiplos comunes?
Todos los números enteros tienen al menos un múltiplo común, que es el producto de los dos números. Sin embargo, este no es necesariamente el MCM. Por ejemplo, el MCM de 7 y 9 es 63, que es el producto de ambos, pero hay múltiples múltiplos comunes menores.
¿Puedo usar el MCM para más de dos números?
¡Claro! El MCM se puede calcular para tres o más números de la misma manera. Simplemente necesitas encontrar los múltiplos o la descomposición en factores primos de todos los números involucrados.
¿Cuál es la diferencia entre MCM y GCD?
El MCM (Mínimo Común Múltiplo) es el menor múltiplo que comparten dos o más números, mientras que el GCD (Máximo Común Divisor) es el mayor divisor que comparten. Ambos son conceptos importantes en matemáticas, pero se utilizan en diferentes contextos.
En resumen, hemos explorado el fascinante mundo del Mínimo Común Múltiplo, específicamente del MCM de 8 y 12. Desde su definición hasta los métodos de cálculo, y sus aplicaciones en la vida diaria, esperamos que este artículo te haya ayudado a entender no solo cómo encontrar el MCM, sino también por qué es útil. La próxima vez que necesites coordinar actividades, ajustar recetas o planificar un evento, recuerda el MCM y cómo puede facilitarte la vida. ¡Hasta la próxima!