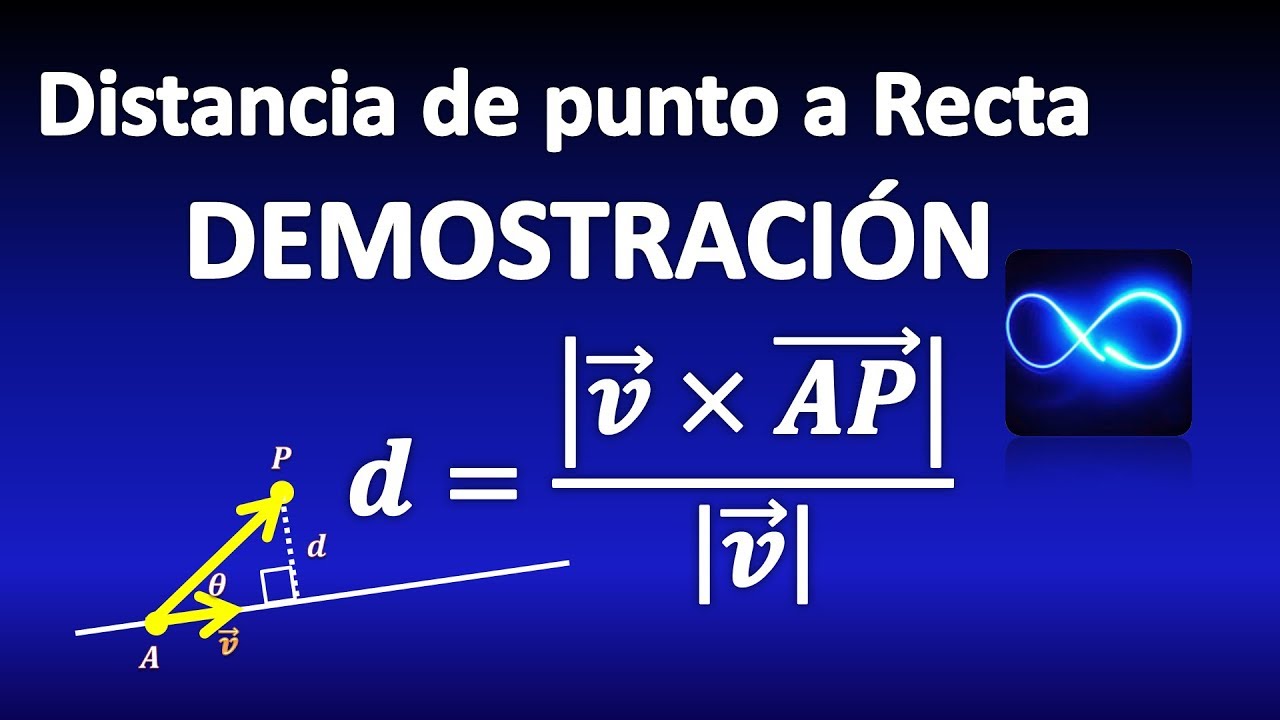
¿Alguna vez te has preguntado cómo medir la distancia entre un punto y una recta en el espacio tridimensional? Bueno, estás en el lugar correcto. Este concepto puede parecer un poco complicado al principio, pero con un poco de práctica y comprensión, ¡te darás cuenta de que es más fácil de lo que parece! Imagina que estás tratando de encontrar la distancia desde un faro (el punto) hasta una línea imaginaria que representa el horizonte (la recta). ¿Cómo lo harías? Vamos a desglosar esto paso a paso.
Entendiendo los Conceptos Básicos
Antes de sumergirnos en los cálculos, es crucial que entendamos algunos conceptos básicos. En el espacio tridimensional, un punto se representa con coordenadas (x, y, z), mientras que una recta se puede definir mediante una ecuación paramétrica o una ecuación cartesiana. Piensa en las coordenadas como un mapa que te dice exactamente dónde está cada punto en el espacio.
Definiendo un Punto y una Recta
Un punto en el espacio tiene tres dimensiones: longitud, ancho y altura. Por ejemplo, el punto A podría estar en (2, 3, 5). Por otro lado, una recta puede definirse de diferentes maneras. Una de las más comunes es la forma paramétrica, donde una recta se expresa como:
R(t) = (x₀ + at, y₀ + bt, z₀ + ct)
En esta ecuación, (x₀, y₀, z₀) son las coordenadas de un punto en la recta, y (a, b, c) son las direcciones en las que la recta se extiende. Es como tener un punto de partida y una dirección en la que ir.
El Método para Calcular la Distancia
Ahora que tenemos claro qué es un punto y una recta, pasemos a la parte emocionante: calcular la distancia. Existen varios métodos para hacerlo, pero aquí te voy a presentar el método más común que involucra un poco de álgebra y geometría. ¡No te preocupes, te guiaré en cada paso!
Determina las Ecuaciones de la Recta
El primer paso es asegurarte de que tienes la ecuación de la recta en la forma adecuada. Si tienes una ecuación paramétrica, asegúrate de que esté claramente definida. Si solo tienes la forma cartesiana, asegúrate de que puedas convertirla a la forma paramétrica si es necesario.
Encuentra un Vector Director
Una vez que tengas la ecuación de la recta, el siguiente paso es encontrar el vector director. Este vector es esencialmente una flecha que apunta en la dirección de la recta. Si tienes la ecuación paramétrica, los coeficientes (a, b, c) son tu vector director. Piensa en él como el camino que seguirías si quisieras moverte a lo largo de la recta.
Crea un Vector desde el Punto a la Recta
Ahora, necesitamos crear un vector que vaya desde el punto (digamos, P) hasta cualquier punto en la recta. Si tomamos un punto en la recta, llamémoslo Q, entonces el vector PQ se puede expresar como:
PQ = Q – P
Esto es como dibujar una línea imaginaria desde tu faro hasta el horizonte. Necesitamos saber cómo se ve esa línea para poder calcular la distancia.
Usando el Producto Cruzado
Una de las maneras más efectivas de calcular la distancia es utilizando el producto cruzado. Este método nos ayuda a encontrar un vector que es perpendicular a ambos, el vector director de la recta y el vector PQ que acabamos de crear. ¡Es como encontrar la sombra más corta del faro en el horizonte!
Calcular el Producto Cruzado
Para calcular el producto cruzado de dos vectores, utilizamos la siguiente fórmula:
U x V = |U||V|sin(θ)
Donde θ es el ángulo entre los dos vectores. En nuestro caso, U sería el vector director de la recta y V sería el vector PQ. El resultado será un nuevo vector que es perpendicular a ambos. Este vector es esencial porque nos ayuda a encontrar la distancia que estamos buscando.
Encontrar la Magnitud del Producto Cruzado
Una vez que tenemos el producto cruzado, el siguiente paso es calcular su magnitud. La magnitud de un vector se puede calcular usando la fórmula:
|V| = √(x² + y² + z²)
Donde x, y y z son las componentes del vector resultante. Esta magnitud representa la longitud de la sombra que proyecta el faro sobre el horizonte.
Calculando la Distancia Final
Finalmente, para encontrar la distancia entre el punto y la recta, utilizamos la siguiente fórmula:
D = |PQ x U| / |U|
Donde D es la distancia que buscamos, PQ es el vector desde el punto a la recta, U es el vector director de la recta, y |U| es la magnitud del vector director. Es como dividir la sombra del faro entre la longitud del horizonte para encontrar la distancia real.
Ejemplo Práctico
Ahora que hemos cubierto los pasos, veamos un ejemplo práctico. Supongamos que tenemos un punto P(1, 2, 3) y una recta definida por la ecuación paramétrica R(t) = (2 + t, 3 + 2t, 4 + 3t). ¿Cómo calcularíamos la distancia entre ellos?
1. Determinar la ecuación de la recta: Ya tenemos la recta en forma paramétrica.
2. Encontrar un vector director: El vector director U es (1, 2, 3).
3. Crear un vector desde P a la recta: Tomamos un punto en la recta, digamos Q(2, 3, 4) cuando t=0, entonces PQ = Q – P = (2 – 1, 3 – 2, 4 – 3) = (1, 1, 1).
4. Calcular el producto cruzado: U x PQ = (1, 2, 3) x (1, 1, 1) = (2-3, 3-1, 1-2) = (-1, 2, -1).
5. Encontrar la magnitud del producto cruzado: |U x PQ| = √((-1)² + 2² + (-1)²) = √(1 + 4 + 1) = √6.
6. Calcular la magnitud del vector director: |U| = √(1² + 2² + 3²) = √(1 + 4 + 9) = √14.
7. Finalmente, la distancia: D = |PQ x U| / |U| = √6 / √14 = √(6/14) = √(3/7).
¡Y ahí lo tienes! Has aprendido cómo calcular la distancia entre un punto y una recta en el espacio tridimensional. Aunque puede parecer complicado al principio, con práctica y paciencia, estos conceptos se volverán mucho más claros. Recuerda, cada vez que te enfrentes a un problema de geometría, descompónlo en pasos más pequeños y trabaja uno por uno. ¡Tú puedes hacerlo!
¿Se puede calcular la distancia entre un punto y una recta en 2D de la misma manera?
¡Sí! El proceso es muy similar, solo que en lugar de trabajar con tres dimensiones, estarías trabajando en un plano bidimensional. Las fórmulas se simplifican un poco, pero la idea básica es la misma.
¿Qué pasa si la recta es vertical?
La dirección de la recta no afecta el método. La distancia se calculará de la misma manera, aunque la orientación del vector director cambiará. Solo asegúrate de seguir los pasos correctamente.
¿Hay alguna aplicación práctica de este cálculo en la vida real?
¡Definitivamente! Este tipo de cálculos se utilizan en campos como la ingeniería, la arquitectura y la navegación. Por ejemplo, al diseñar edificios, es esencial saber la distancia entre diferentes puntos y estructuras para asegurar que todo esté alineado correctamente.
¿Es necesario conocer el álgebra para entender esto?
Un conocimiento básico de álgebra y geometría te ayudará mucho, pero no te preocupes si no eres un experto. Con práctica y paciencia, ¡todo se vuelve más fácil!
¿Puedo usar software para hacer estos cálculos?
Claro, hay muchas herramientas de software y calculadoras en línea que pueden ayudarte a realizar estos cálculos. Sin embargo, entender el proceso detrás de ellos te dará una mejor comprensión de lo que estás haciendo.