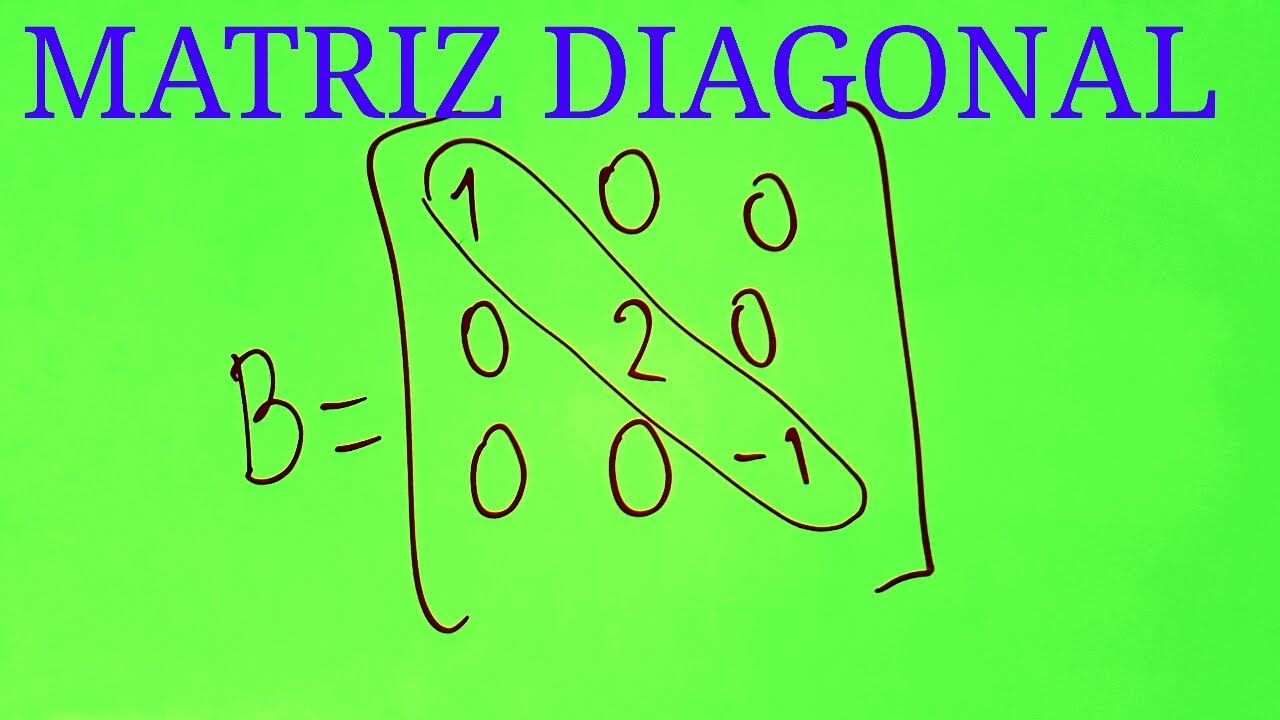
Las matrices son un concepto fundamental en matemáticas y, en particular, en álgebra lineal. Una matriz diagonal es una de esas estructuras que, aunque puede parecer simple a primera vista, posee propiedades fascinantes y aplicaciones en diversos campos. Pero, ¿qué es exactamente una matriz diagonal? Imagina una cuadrícula, donde solo hay números en la diagonal que va desde la esquina superior izquierda hasta la esquina inferior derecha, mientras que todos los demás elementos son ceros. Esta disposición no solo es visualmente atractiva, sino que también tiene implicaciones importantes en cálculos y transformaciones. En este artículo, vamos a desglosar la definición de matrices diagonales, sus propiedades, y veremos algunos ejemplos que nos ayudarán a entender mejor su funcionamiento y su utilidad.
Definición de Matriz Diagonal
En términos simples, una matriz diagonal es una matriz cuadrada donde todos los elementos fuera de la diagonal principal son cero. Por ejemplo, considera la siguiente matriz:
| 5 0 0 | | 0 3 0 | | 0 0 8 |
En este caso, los números 5, 3 y 8 están en la diagonal, mientras que todos los demás elementos son ceros. Esta estructura tan limpia permite realizar operaciones matemáticas de manera más sencilla. En el mundo de las matrices, la diagonal se convierte en el foco de atención, y los ceros alrededor nos dan un respiro al simplificar cálculos.
Propiedades de las Matrices Diagonales
Multiplicación de Matrices Diagonales
Una de las propiedades más interesantes de las matrices diagonales es cómo se comportan durante la multiplicación. Si multiplicamos dos matrices diagonales, el resultado también será una matriz diagonal. Por ejemplo, si tenemos:
A = | 2 0 0 | B = | 4 0 0 |
| 0 3 0 | | 0 5 0 |
| 0 0 6 | | 0 0 7 |
El producto AB será:
AB = | 2*4 0 0 | = | 8 0 0 |
| 0 3*5 0 | | 0 15 0 |
| 0 0 6*7 | | 0 0 42 |
Como puedes ver, la multiplicación se realiza solo en la diagonal, lo que facilita el proceso. ¡Es como si las matrices se llevaran bien y decidieran no complicarse la vida!
Determinante de una Matriz Diagonal
Otra propiedad clave es el cálculo del determinante. El determinante de una matriz diagonal es simplemente el producto de los elementos en su diagonal. Por ejemplo, para la matriz que mencionamos anteriormente:
| 5 0 0 | | 0 3 0 | | 0 0 8 |
El determinante sería 5 * 3 * 8 = 120. Esta característica es muy útil porque nos permite calcular determinantes de manera rápida sin tener que hacer cálculos complejos.
Inversa de una Matriz Diagonal
Las matrices diagonales también son elegantes cuando se trata de encontrar su inversa. Si todos los elementos de la diagonal son diferentes de cero, la inversa de una matriz diagonal también será diagonal. Si tomamos nuestra matriz anterior:
A = | 5 0 0 |
| 0 3 0 |
| 0 0 8 |
Su inversa sería:
A⁻¹ = | 1/5 0 0 |
| 0 1/3 0 |
| 0 0 1/8 |
Esto es realmente útil en álgebra lineal, donde encontrar la inversa de una matriz puede ser una tarea complicada. Las matrices diagonales nos ahorran tiempo y esfuerzo.
Ejemplos Prácticos de Matrices Diagonales
Ejemplo 1: Transformación de Coordenadas
Las matrices diagonales son frecuentemente utilizadas en transformaciones de coordenadas. Imagina que quieres escalar un objeto en un gráfico. Puedes usar una matriz diagonal para hacer esto de manera eficiente. Por ejemplo, si deseas escalar un objeto por 2 en el eje x y por 3 en el eje y, puedes usar la siguiente matriz:
| 2 0 | | 0 3 |
Cuando multiplicas esta matriz por las coordenadas del objeto, obtendrás un nuevo conjunto de coordenadas escaladas. Esto es mucho más rápido que calcular cada coordenada individualmente, ¿verdad?
Ejemplo 2: Resolviendo Sistemas de Ecuaciones
Otra aplicación interesante es en la resolución de sistemas de ecuaciones lineales. Si tienes un sistema que se puede expresar en forma matricial, las matrices diagonales simplifican enormemente el proceso. Por ejemplo, considera el sistema:
2x = 4 3y = 9
Esto se puede escribir como:
| 2 0 | | x | = | 4 | | 0 3 | | y | | 9 |
Al resolver, es fácil despejar x e y directamente al dividir ambos lados por los coeficientes en la diagonal. Este es un gran ejemplo de cómo las matrices diagonales pueden facilitar la vida.
¿Por qué son importantes las Matrices Diagonales?
Las matrices diagonales no solo son una curiosidad matemática, sino que tienen aplicaciones en campos tan diversos como la física, la economía y la informática. Desde la representación de transformaciones en gráficos por computadora hasta la solución de sistemas de ecuaciones en ingeniería, estas matrices son esenciales. Su simplicidad las hace ideales para cálculos rápidos y eficientes, lo que es crucial en situaciones donde el tiempo y la precisión son fundamentales.
¿Qué sucede si hay ceros en la diagonal de una matriz diagonal?
Si hay ceros en la diagonal, la matriz sigue siendo diagonal, pero no será invertible. Esto significa que no podrás encontrar su inversa, lo que puede ser un inconveniente en ciertos cálculos.
¿Las matrices diagonales son siempre cuadradas?
Sí, las matrices diagonales siempre son cuadradas. Esto se debe a que la diagonal principal solo tiene sentido en el contexto de matrices cuadradas, donde el número de filas es igual al número de columnas.
¿Cómo se pueden utilizar las matrices diagonales en programación?
En programación, las matrices diagonales se pueden utilizar para optimizar cálculos en algoritmos que requieren transformaciones de datos o que resuelven sistemas de ecuaciones. Al usar estructuras de datos que representan matrices diagonales, puedes reducir el uso de memoria y aumentar la velocidad de ejecución.
¿Existen aplicaciones de matrices diagonales en la vida diaria?
¡Definitivamente! Desde la programación de gráficos en videojuegos hasta la optimización de rutas en logística, las matrices diagonales juegan un papel crucial en muchos aspectos de nuestra vida cotidiana. Son como el “héroe oculto” en el trasfondo de muchas tecnologías modernas.
¿Qué otros tipos de matrices existen?
Además de las matrices diagonales, existen matrices simétricas, matrices triangulares y matrices ortogonales, entre otras. Cada tipo tiene sus propias propiedades y aplicaciones específicas, lo que las hace interesantes para estudiar en álgebra lineal.
En resumen, las matrices diagonales son más que simples arreglos de números; son herramientas poderosas que simplifican cálculos y tienen aplicaciones en una variedad de campos. Desde su definición hasta sus propiedades y ejemplos prácticos, espero que este artículo te haya ayudado a entender mejor el fascinante mundo de las matrices diagonales. ¿Te animas a seguir explorando este tema y descubrir más sobre el álgebra lineal?