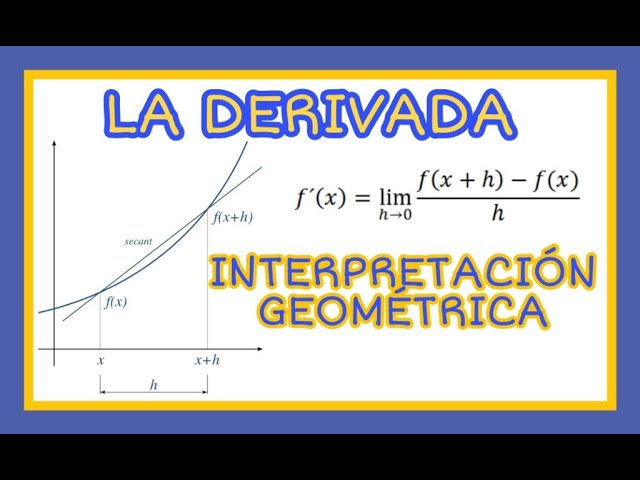
¿Qué es la derivada y por qué es importante?
La derivada es un concepto fundamental en el cálculo que nos ayuda a entender cómo cambian las cosas. Imagina que estás conduciendo un coche y quieres saber a qué velocidad te mueves en un momento específico. La velocidad es una derivada de la posición respecto al tiempo. En términos simples, la derivada nos da la tasa de cambio de una función. Pero, ¿qué significa esto en un contexto más visual? Aquí es donde entra la interpretación geométrica. Vamos a sumergirnos en el fascinante mundo de las derivadas y descubrir su significado y aplicaciones.
La Derivada como Pendiente de una Recta Tangente
Visualiza que tienes una curva en un gráfico. Ahora, si quisieras saber cuán empinada es esa curva en un punto específico, la derivada se convierte en tu mejor amiga. La derivada en un punto dado nos dice la pendiente de la recta tangente a la curva en ese punto. ¿Alguna vez has intentado escalar una montaña? La pendiente de la montaña te diría cuán difícil es escalar en ese lugar. Si la pendiente es alta, ¡prepárate para un esfuerzo considerable! De igual manera, una pendiente baja significa que el camino es más fácil.
Rectas Tangentes y Su Relación con la Derivada
La recta tangente es como un amigo que te da un empujón en la dirección correcta cuando te sientes perdido. Toca la curva en un solo punto y refleja cómo se comporta la curva en ese instante. Si piensas en una montaña rusa, la derivada te dice si estás subiendo o bajando en un momento específico. Cuando la derivada es positiva, ¡estás subiendo! Si es negativa, estás en una bajada. Y si es cero, ¡estás en la cima o en un punto de inflexión! Esta es una forma increíble de visualizar cómo cambian las cosas.
Aplicaciones de la Derivada en la Vida Real
Ahora que entendemos la geometría detrás de la derivada, es hora de ver cómo se aplica en la vida real. Las derivadas no son solo para matemáticos; son herramientas poderosas en diversas disciplinas. Desde la física hasta la economía, la derivada nos ayuda a tomar decisiones informadas. Por ejemplo, en economía, la derivada puede representar cómo cambia el costo en relación con la producción. Si estás produciendo un artículo y quieres saber cuánto costará producir una unidad más, ¡la derivada te lo dirá!
Derivadas en la Física
En el mundo de la física, la derivada es esencial. Cuando hablamos de velocidad, realmente estamos hablando de la derivada de la posición con respecto al tiempo. Si lanzas una pelota al aire, la derivada de su altura con respecto al tiempo te dice cuán rápido está subiendo o bajando en cada instante. Y si quieres saber la aceleración, simplemente tomas la derivada de la velocidad. ¡Es un juego de dominó donde cada parte se conecta con la siguiente!
Interpretación Gráfica de la Derivada
La representación gráfica de la derivada es fundamental para entender su significado. Cuando dibujas una función en un gráfico, la derivada en un punto específico es la pendiente de la línea tangente a esa curva. Imagina que estás en un parque y hay una montaña. La línea tangente en la cima de la montaña te dirá cuán empinada es la subida. Si dibujas la curva y la línea tangente, puedes ver claramente cómo la derivada representa la inclinación en ese punto.
Ejemplo Práctico: La Curva de Crecimiento
Supongamos que estás analizando el crecimiento de una planta. La altura de la planta en función del tiempo puede ser representada por una curva en un gráfico. La derivada en un momento específico te dirá cuán rápido está creciendo la planta en ese instante. Si la derivada es grande, ¡fantástico! La planta está creciendo rápidamente. Pero si es pequeña, quizás necesite un poco más de agua o sol. Esta interpretación visual te ayuda a tomar decisiones más informadas sobre el cuidado de la planta.
Derivadas y Optimización
Una de las aplicaciones más emocionantes de las derivadas es en el campo de la optimización. Aquí es donde las cosas se ponen realmente interesantes. Imagina que estás tratando de encontrar el punto más alto de una montaña o el punto más bajo de un valle. En términos matemáticos, esto significa encontrar los máximos y mínimos de una función. Para hacerlo, necesitas encontrar los puntos donde la derivada es cero. Estos puntos son candidatos para ser máximos o mínimos.
El Método de la Primera Derivada
El método de la primera derivada es como tener un mapa del tesoro. Primero, encuentras la derivada de la función. Luego, estableces la derivada igual a cero para encontrar los puntos críticos. Después, puedes analizar la concavidad de la función para determinar si esos puntos son máximos, mínimos o puntos de inflexión. Es como tener un detector de metales en una búsqueda del tesoro: te guía hacia los lugares donde es más probable que encuentres algo valioso.
La Segunda Derivada: Profundizando en la Curva
La segunda derivada lleva la interpretación de la derivada a un nivel más profundo. Mientras que la primera derivada te dice la pendiente de la función, la segunda derivada te dice cómo está cambiando esa pendiente. Es como tener una lupa que te permite ver los detalles más finos de la curva. Si la segunda derivada es positiva, la función está «sonriendo» (concavidad hacia arriba). Si es negativa, está «frunciendo el ceño» (concavidad hacia abajo).
Aplicaciones de la Segunda Derivada
La segunda derivada es útil en varios contextos. En economía, puede ayudarte a entender cómo cambia la tasa de crecimiento de una función de costo. En física, te da información sobre la aceleración de un objeto. En general, la segunda derivada te ayuda a analizar la estabilidad de los puntos críticos que encontraste anteriormente. Es como tener un segundo par de ojos que te ayudan a ver el panorama completo.
Ejemplos de Derivadas en Diversas Disciplinas
Las derivadas tienen aplicaciones en casi todas las disciplinas. Vamos a explorar algunas de ellas para ver cuán amplias son sus aplicaciones. En biología, la derivada puede representar la tasa de cambio de la población de una especie en un ecosistema. En ingeniería, se utilizan para optimizar diseños y estructuras. En meteorología, ayudan a modelar y predecir cambios en el clima. Las posibilidades son prácticamente infinitas.
Derivadas en la Biología
En biología, el crecimiento de las poblaciones se puede modelar mediante funciones. La derivada puede decirte cómo cambia la población con el tiempo. Si la población está creciendo rápidamente, la derivada será positiva. Si hay una disminución, la derivada será negativa. Esto es crucial para entender la dinámica de las poblaciones y para tomar decisiones sobre conservación y manejo de recursos.
¿Por Qué Deberías Importarte la Derivada?
Ahora que hemos explorado la derivada desde diferentes ángulos, es importante preguntarnos: ¿por qué debería importarte? Las derivadas son herramientas poderosas que te permiten entender el mundo que te rodea. Desde la economía hasta la biología, te ayudan a tomar decisiones informadas. Te permiten ver patrones y cambios, dándote una ventaja en cualquier campo que elijas.
La derivada es más que un concepto matemático; es una forma de ver y entender el mundo. A través de la interpretación geométrica, podemos visualizar cómo cambian las cosas y cómo podemos utilizar ese conocimiento para mejorar nuestras vidas y las decisiones que tomamos. Así que la próxima vez que escuches la palabra «derivada», recuerda que no es solo una herramienta matemática; es una clave para desentrañar los misterios del cambio.
¿Qué es una derivada en términos simples?
La derivada es la tasa de cambio de una función en un punto específico. Te dice cuán rápido cambia el valor de la función en ese punto.
¿Cómo se interpreta geométricamente una derivada?
Geométricamente, la derivada en un punto es la pendiente de la recta tangente a la curva en ese punto. Indica si la función está subiendo, bajando o es constante.
¿Por qué son importantes las derivadas en la vida real?
Las derivadas tienen aplicaciones en diversas disciplinas, como la física, la economía y la biología, ayudando a entender y predecir cambios en diferentes contextos.
¿Qué es la segunda derivada y por qué debería importarme?
La segunda derivada nos dice cómo está cambiando la pendiente de la función. Es útil para identificar la concavidad y analizar la estabilidad de los puntos críticos.
¿Puedo usar derivadas si no soy matemático?
¡Absolutamente! Las derivadas son herramientas útiles en muchas áreas, y entender su concepto básico puede ayudarte a tomar decisiones más informadas en tu vida diaria.