Las derivadas son una herramienta fundamental en el mundo del cálculo. Pero, ¿alguna vez te has preguntado por qué son tan importantes? Imagina que estás conduciendo un coche. La derivada es como el velocímetro que te dice cuán rápido estás yendo en un momento específico. Al entender las derivadas, no solo puedes analizar la velocidad de cambio, sino que también puedes predecir comportamientos futuros en una variedad de contextos, desde la economía hasta la física. En este artículo, vamos a explorar cómo puedes mejorar tu comprensión de las derivadas a través de ejercicios prácticos y ejemplos que te ayudarán a afianzar tus conocimientos.
¿Qué Son las Derivadas y Cómo Funcionan?
Para comenzar, es crucial tener una idea clara de qué son las derivadas. En términos simples, la derivada de una función mide cómo cambia el valor de esa función cuando se altera ligeramente su variable independiente. Si te resulta más fácil, piensa en las derivadas como una forma de medir la pendiente de una curva en un punto específico. ¿Recuerdas esas montañas rusas? La pendiente de la montaña rusa en un punto dado te dirá si vas hacia arriba o hacia abajo. Así es como funcionan las derivadas: te indican la dirección y la velocidad del cambio.
Definición Formal de Derivadas
Matemáticamente, la derivada se define como el límite de la tasa de cambio promedio de una función a medida que el intervalo de cambio se aproxima a cero. Es un concepto que puede parecer complicado al principio, pero una vez que lo desglosas, se vuelve más accesible. La notación comúnmente utilizada para la derivada de una función ( f(x) ) es ( f'(x) ) o ( frac{df}{dx} ). Aquí, ( f'(x) ) representa la derivada de ( f ) con respecto a ( x ).
Ejercicios Prácticos para Entender las Derivadas
Ahora que tenemos una comprensión básica de lo que son las derivadas, es hora de poner en práctica este conocimiento. Aquí te propongo algunos ejercicios que puedes realizar para mejorar tu comprensión. No te preocupes si no entiendes todo de inmediato; lo importante es practicar y familiarizarte con los conceptos.
Ejercicio 1: Derivadas de Funciones Polinómicas
Comencemos con un ejercicio simple. Considera la función ( f(x) = 3x^2 + 2x + 1 ). Tu tarea es encontrar la derivada de esta función. Para hacerlo, aplicamos la regla de potencia, que establece que si tienes ( ax^n ), la derivada es ( n cdot ax^{n-1} ). Así que, al aplicar esto:
- La derivada de ( 3x^2 ) es ( 6x ).
- La derivada de ( 2x ) es ( 2 ).
- La derivada de ( 1 ) es ( 0 ).
Por lo tanto, ( f'(x) = 6x + 2 ). ¡Felicidades! Has calculado tu primera derivada.
Ejercicio 2: Aplicación de la Regla del Producto
Ahora, probemos algo un poco más complicado. Supongamos que tienes dos funciones, ( u(x) = x^2 ) y ( v(x) = sin(x) ). La derivada del producto de estas funciones se calcula usando la regla del producto, que dice que ( (uv)’ = u’v + uv’ ). Primero, encontramos las derivadas de ( u ) y ( v ):
- La derivada de ( u(x) = x^2 ) es ( u'(x) = 2x ).
- La derivada de ( v(x) = sin(x) ) es ( v'(x) = cos(x) ).
Ahora, aplicamos la regla del producto:
Así que ( (uv)’ = (2x)(sin(x)) + (x^2)(cos(x)) ). Este ejercicio no solo te ayuda a practicar la derivación, sino que también te familiariza con el uso de diferentes reglas.
Más Ejercicios para Profundizar en el Tema
A medida que te sientas más cómodo con las derivadas, puedes comenzar a abordar ejercicios más desafiantes. Aquí hay algunos ejemplos que puedes intentar:
Ejercicio 3: Derivadas de Funciones Trigonométricas
Calcula la derivada de la función ( f(x) = tan(x) + cos(x) ). Recuerda que la derivada de ( tan(x) ) es ( sec^2(x) ) y la de ( cos(x) ) es ( -sin(x) ). Por lo tanto:
La derivada ( f'(x) = sec^2(x) – sin(x) ).
Ejercicio 4: Derivadas de Funciones Exponenciales
Ahora, considera la función ( g(x) = e^{2x} ). Aquí, puedes usar la regla de la cadena. La derivada de ( e^{u} ) es ( e^{u} cdot u’ ), donde ( u = 2x ). Entonces, ( g'(x) = e^{2x} cdot 2 = 2e^{2x} ).
Consejos para Practicar Derivadas
Practicar derivadas puede ser un desafío, pero hay algunas estrategias que pueden ayudarte a mejorar:
Comprende las Reglas
Familiarízate con las diferentes reglas de derivación, como la regla de la suma, la regla del producto, la regla del cociente y la regla de la cadena. Tener un buen dominio de estas reglas te facilitará mucho el trabajo.
Resuelve Problemas Variados
No te limites a un solo tipo de función. Practica con polinómicas, trigonométricas, exponenciales y logarítmicas. Cuanto más amplio sea tu rango de práctica, más preparado estarás.
Usa Recursos en Línea
Hay muchos recursos en línea, desde videos explicativos hasta foros de discusión donde puedes hacer preguntas y obtener respuestas. No dudes en utilizarlos. Aprender en comunidad puede ser muy enriquecedor.
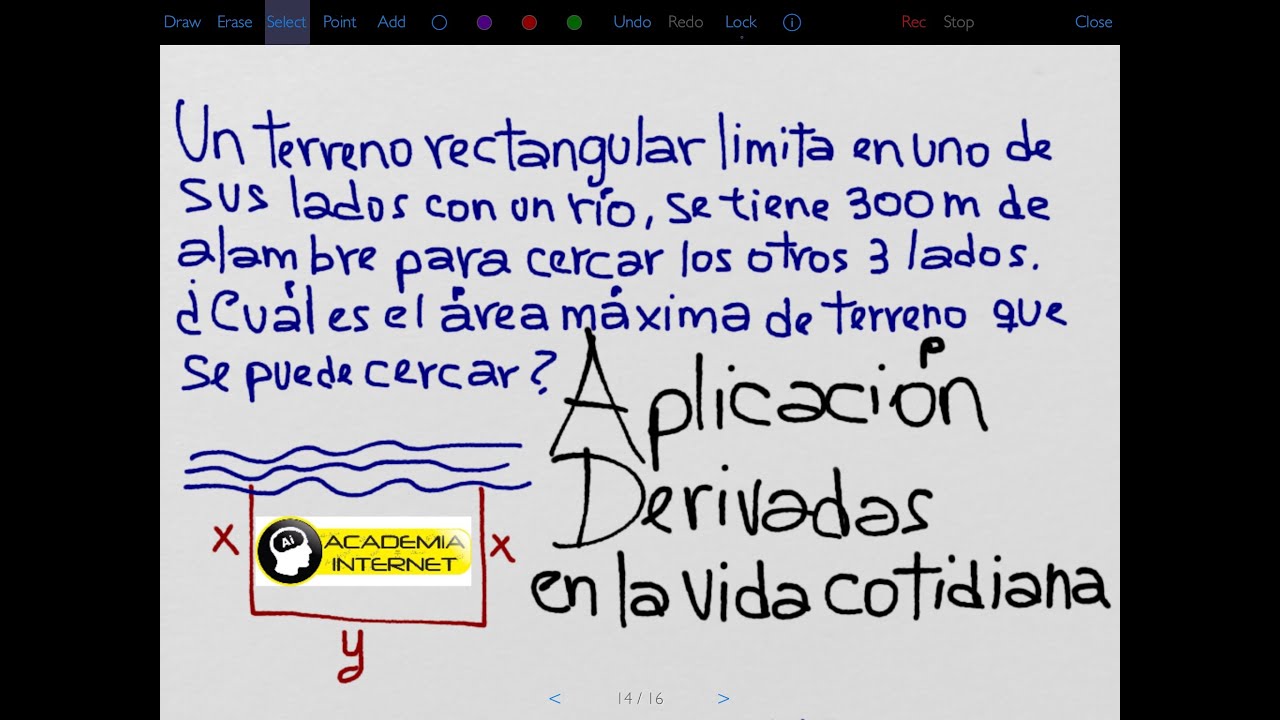
Aplicaciones Prácticas de las Derivadas
Ahora que ya has practicado y entendido cómo funcionan las derivadas, es hora de ver cómo se aplican en la vida real. Las derivadas no son solo un concepto abstracto; tienen aplicaciones prácticas en diversas áreas:
Economía
En economía, las derivadas se utilizan para analizar cómo los cambios en el precio afectan la oferta y la demanda. Por ejemplo, si tienes una función de ingresos, la derivada te dirá cómo cambiará el ingreso si alteras el precio de un producto.
Física
En física, las derivadas se utilizan para describir el movimiento. La velocidad es la derivada de la posición con respecto al tiempo, y la aceleración es la derivada de la velocidad. Esto permite a los físicos modelar el movimiento de los objetos de manera precisa.
Biología
En biología, las derivadas pueden ayudar a modelar el crecimiento de poblaciones. Por ejemplo, si conoces la tasa de crecimiento de una población, puedes usar derivadas para predecir cuántos individuos habrá en el futuro.
Las derivadas son una herramienta poderosa que, aunque puede parecer intimidante al principio, se vuelve más accesible con la práctica. Recuerda que la clave está en hacer ejercicios variados y entender las reglas que rigen su aplicación. Así que, ¿por qué no te desafías a ti mismo y comienzas a resolver algunos problemas hoy mismo? ¡Tu futuro yo te lo agradecerá!
- ¿Por qué es importante entender las derivadas? Las derivadas son esenciales para comprender cómo cambian las funciones, lo que tiene aplicaciones en diversas áreas como la economía, la física y la biología.
- ¿Cuáles son las principales reglas de derivación que debo conocer? Las reglas más importantes incluyen la regla de la suma, la regla del producto, la regla del cociente y la regla de la cadena.
- ¿Dónde puedo encontrar más ejercicios de derivadas? Puedes encontrar ejercicios en libros de texto, sitios web educativos y plataformas en línea que ofrecen problemas de práctica.
- ¿Las derivadas tienen aplicaciones en la vida diaria? Sí, las derivadas se utilizan en muchas áreas, desde la economía hasta la biología, para modelar y entender cambios en diferentes contextos.