¿Alguna vez te has preguntado cómo se comportan las funciones matemáticas? Imagina que las funciones son como montañas y valles en un paisaje. Algunas suben hacia el cielo (crecimiento) y otras bajan hacia el suelo (decrecimiento). En este artículo, exploraremos en detalle cómo determinar el crecimiento y el decrecimiento de una función, y por qué es fundamental entender estos conceptos en matemáticas y en la vida cotidiana. Vamos a desglosar este tema en partes más pequeñas, como si estuviéramos armando un rompecabezas. ¿Listo? ¡Empecemos!
¿Qué es el Crecimiento y Decrecimiento de una Función?
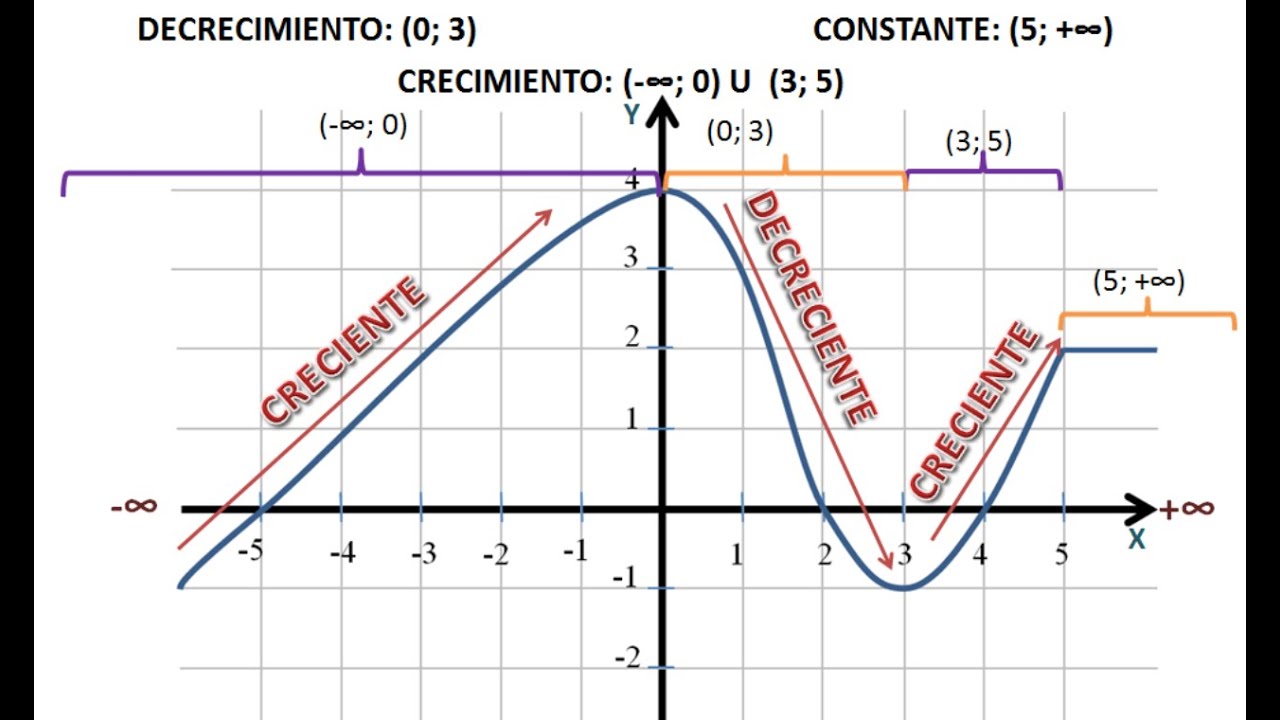
Para comenzar, definamos qué significa que una función esté creciendo o decreciendo. En términos simples, una función está en crecimiento en un intervalo cuando, a medida que avanzamos hacia la derecha en el eje x, los valores de la función (eje y) aumentan. Por otro lado, una función está en decrecimiento cuando, al movernos hacia la derecha, los valores de la función disminuyen. ¡Así de fácil!
Imagina que estás subiendo una montaña: cada paso que das hacia la derecha te lleva a un lugar más alto. Eso es crecimiento. Ahora, piensa en un descenso: cada paso hacia la derecha te lleva a un lugar más bajo. Eso es decrecimiento. ¿Ves cómo estas ideas son bastante intuitivas?
Identificando el Crecimiento y Decrecimiento
Derivadas: Tu Mejor Amiga
Para identificar dónde una función crece o decrece, utilizamos la derivada. La derivada de una función nos dice la pendiente de la curva en un punto específico. Si la derivada es positiva, la función está creciendo; si es negativa, está decreciendo. ¡Es como tener un mapa que te guía en tu viaje a través de la montaña!
Por ejemplo, si tienes una función f(x) y calculas su derivada f'(x), y encuentras que f'(x) > 0 en un intervalo, eso significa que la función está creciendo en ese intervalo. Por otro lado, si f'(x) < 0, la función está decreciendo. Entonces, la clave aquí es analizar la derivada y ver dónde cambia de signo.
Puntos Críticos: Donde Cambia el Juego
Los puntos críticos son esos lugares en los que la derivada es cero o no está definida. Aquí es donde la función puede cambiar de crecer a decrecer o viceversa. Para encontrar estos puntos, simplemente igualamos la derivada a cero y resolvemos para x.
Pero no te preocupes, no necesitas una calculadora científica para esto. Solo necesitas un poco de paciencia y práctica. Una vez que encuentres estos puntos críticos, puedes hacer un análisis de intervalos para determinar el comportamiento de la función en diferentes secciones del eje x.
Ejemplo Práctico: Una Función Cuadrática
Veamos un ejemplo concreto. Supongamos que tenemos la función f(x) = -x^2 + 4x. Primero, vamos a calcular su derivada:
f'(x) = -2x + 4.
Ahora, igualamos la derivada a cero para encontrar los puntos críticos:
-2x + 4 = 0
2x = 4
x = 2.
Ahora que tenemos nuestro punto crítico en x = 2, necesitamos analizar el comportamiento de la función en los intervalos (-∞, 2) y (2, ∞).
Para x < 2, por ejemplo, probemos con x = 1: f'(1) = -2(1) + 4 = 2 (positivo, por lo tanto, está creciendo). Para x > 2, probemos con x = 3:
f'(3) = -2(3) + 4 = -2 (negativo, por lo tanto, está decreciendo).
Así que podemos concluir que la función está creciendo en el intervalo (-∞, 2) y decreciendo en el intervalo (2, ∞). ¡Y así es como se hace!
Gráficos: La Visualización es Clave
Una imagen vale más que mil palabras, ¿verdad? Cuando trabajamos con funciones, los gráficos son herramientas poderosas. Nos permiten visualizar el crecimiento y el decrecimiento de manera clara. Al graficar la función f(x) = -x^2 + 4x, verás que efectivamente hay un pico en x = 2, lo que confirma que antes de ese punto la función está creciendo y después está decreciendo.
Recuerda que los gráficos no solo son para los matemáticos. También pueden ser útiles en muchas áreas de la vida, desde la economía hasta la biología. ¿Quién no ha visto un gráfico de crecimiento de ventas o el aumento de la población a lo largo del tiempo?
Aplicaciones del Crecimiento y Decrecimiento de Funciones
En el Mundo Real
Entender el crecimiento y decrecimiento de funciones tiene aplicaciones prácticas en diversas áreas. Por ejemplo, en economía, podemos analizar cómo los precios cambian con el tiempo. En biología, podemos estudiar el crecimiento de poblaciones y cómo estas pueden decrecer debido a factores ambientales.
Imagina que eres un empresario y quieres saber cuándo tus ventas alcanzarán su punto máximo. Al analizar la función de tus ventas, puedes prever cuándo será ese momento y tomar decisiones informadas sobre tus estrategias de marketing.
En la Ciencia y la Ingeniería
En campos como la física y la ingeniería, el crecimiento y el decrecimiento de funciones son esenciales para entender conceptos como la velocidad y la aceleración. La relación entre la posición de un objeto y el tiempo puede ser modelada por funciones que crecen o decrecen, dependiendo de cómo se mueve el objeto.
Por ejemplo, si lanzas una pelota al aire, su altura (posición) en función del tiempo es una parábola que primero crece (sube) y luego decrece (baja). Entender este comportamiento puede ayudarte a calcular la altura máxima que alcanzará la pelota o el tiempo que tardará en caer.
En resumen, el crecimiento y el decrecimiento de una función son conceptos fundamentales en matemáticas que tienen un impacto significativo en el mundo que nos rodea. Ya sea que estés analizando una función cuadrática o explorando un fenómeno en la naturaleza, comprender cómo se comportan estas funciones te proporcionará una herramienta poderosa para hacer predicciones y tomar decisiones.
Así que, la próxima vez que veas una función, recuerda que detrás de esos números y letras hay una historia de crecimiento y decrecimiento, como una montaña rusa de emociones. ¿Te atreves a explorarla?
¿Qué es una función creciente?
Una función creciente es aquella en la que, a medida que aumentamos el valor de x, el valor de la función (y) también aumenta. Esto significa que la pendiente de la función es positiva en ese intervalo.
¿Cómo se puede determinar si una función es decreciente?
Para determinar si una función es decreciente, se debe calcular la derivada de la función. Si la derivada es negativa en un intervalo, eso indica que la función está decreciendo en ese intervalo.
¿Qué son los puntos críticos y por qué son importantes?
Los puntos críticos son valores de x donde la derivada de la función es cero o no está definida. Son importantes porque indican posibles cambios en el comportamiento de la función, como pasar de crecer a decrecer.
¿Existen funciones que no crecen ni decrecen?
Sí, existen funciones constantes que no cambian su valor, independientemente de los cambios en x. En este caso, la derivada es cero en todo el dominio de la función.
¿Por qué es importante entender el crecimiento y decrecimiento de funciones?
Entender el crecimiento y decrecimiento de funciones es crucial en muchas disciplinas, como la economía, la biología y la ingeniería, ya que nos permite hacer predicciones, tomar decisiones informadas y comprender mejor los fenómenos del mundo real.