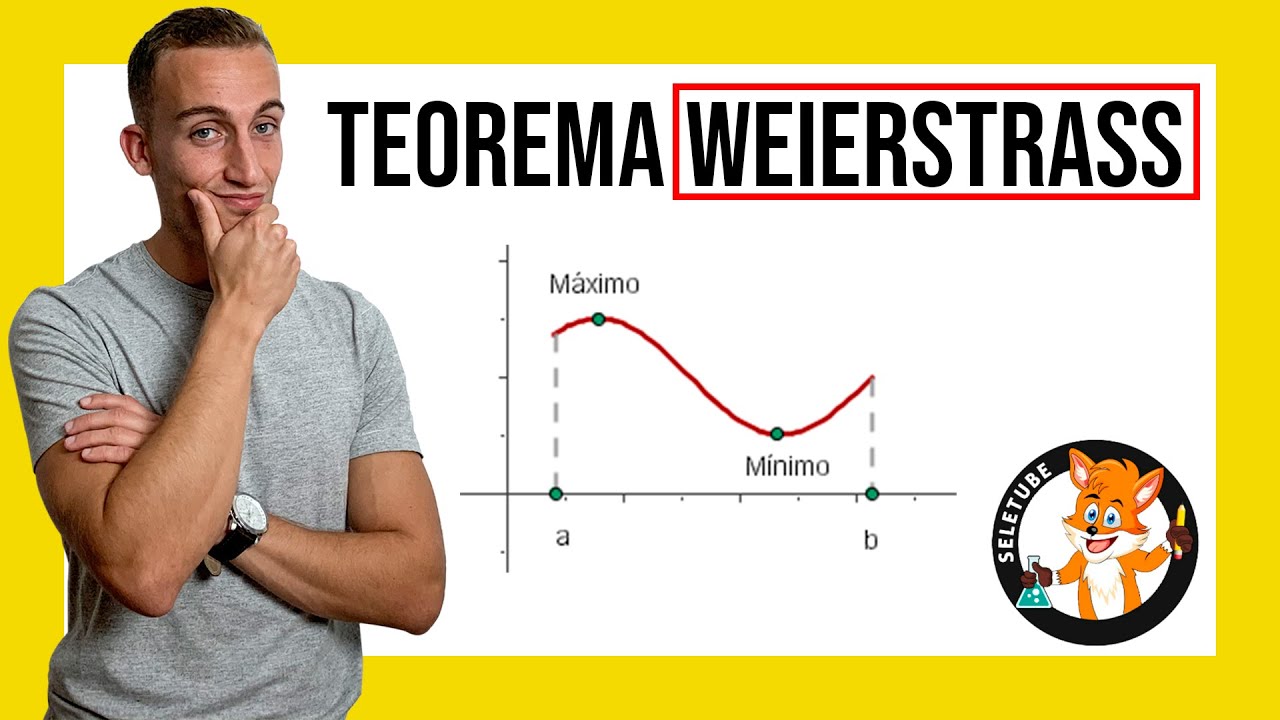
El Teorema de Weierstrass es una de esas joyas matemáticas que, aunque puede parecer un poco intimidante al principio, es esencial para entender el análisis matemático. Imagina que estás en un vasto océano de funciones y límites, y de repente, encuentras un faro que te guía. Eso es exactamente lo que hace este teorema. Nos dice que en cualquier intervalo cerrado y acotado, una función continua alcanza su máximo y mínimo. Suena sencillo, ¿verdad? Pero, ¿qué significa realmente en términos prácticos? En este artículo, vamos a desglosar este teorema y resolver algunos ejercicios para que puedas verlo en acción. Así que prepárate para sumergirte en el fascinante mundo de las matemáticas.
¿Qué es el Teorema de Weierstrass?
Para entender el Teorema de Weierstrass, primero necesitamos desmenuzarlo. Este teorema se basa en dos conceptos clave: la continuidad y los intervalos cerrados y acotados. ¿Alguna vez has visto una montaña? Imagina que la cima de la montaña es el máximo y el valle es el mínimo. El teorema nos asegura que, en cualquier montaña que dibujes, habrá un punto más alto y un punto más bajo, siempre que te limites a un intervalo cerrado. Esto es crucial en el análisis porque nos permite garantizar que ciertas propiedades se cumplen en situaciones específicas.
Definiciones Clave
Antes de continuar, es importante aclarar algunos términos. Una función es continua si no tiene saltos o interrupciones; puedes dibujar su gráfico sin levantar el lápiz del papel. Un intervalo cerrado es aquel que incluye sus extremos, como [a, b], donde a y b son los límites. Por último, un intervalo acotado significa que hay límites finitos a la función, es decir, no se extiende hacia el infinito.
Ejercicios Resueltos
Ahora que tenemos una buena base, ¡es hora de poner en práctica lo que hemos aprendido! Vamos a resolver algunos ejercicios que nos ayudarán a aplicar el Teorema de Weierstrass.
Ejercicio 1: Función Lineal
Consideremos la función f(x) = 2x + 3 en el intervalo [1, 4]. Primero, evaluamos la función en los extremos del intervalo:
- f(1) = 2(1) + 3 = 5
- f(4) = 2(4) + 3 = 11
Como esta es una función lineal, sabemos que no tiene máximos o mínimos en el interior del intervalo. Por lo tanto, el máximo es 11 y el mínimo es 5. ¿Ves cómo el teorema se aplica aquí? No importa lo que hagas, siempre habrá un punto más alto y uno más bajo en ese intervalo.
Ejercicio 2: Función Cuadrática
Ahora, probemos con una función cuadrática: g(x) = -x² + 4x en el intervalo [0, 4]. Primero, necesitamos encontrar los extremos y el vértice de la parábola, que se da por la fórmula x = -b/(2a). En este caso, a = -1 y b = 4:
- x = -4/(2 * -1) = 2
Ahora evaluamos g(x) en los puntos relevantes: 0, 2 y 4:
- g(0) = -0² + 4(0) = 0
- g(2) = -2² + 4(2) = 8
- g(4) = -4² + 4(4) = 0
Así que tenemos g(0) = 0, g(2) = 8 y g(4) = 0. El máximo es 8 y el mínimo es 0. Nuevamente, el Teorema de Weierstrass nos asegura que estos valores existen dentro del intervalo cerrado y acotado.
Aplicaciones Prácticas del Teorema de Weierstrass
El Teorema de Weierstrass no es solo un ejercicio académico; tiene aplicaciones en el mundo real. Desde la economía hasta la ingeniería, este teorema se utiliza para optimizar funciones, modelar comportamientos y tomar decisiones informadas. Por ejemplo, si estás tratando de maximizar las ganancias de un negocio, querrás encontrar el precio que maximiza tus ingresos. El Teorema de Weierstrass te dice que hay un precio óptimo que puedes encontrar dentro de un rango específico.
Ejemplo en Economía
Imagina que tienes una función de ingreso I(p) = -p² + 10p, donde p es el precio del producto. Si deseas maximizar tus ingresos, puedes aplicar el Teorema de Weierstrass en el intervalo [0, 10]. Al encontrar el vértice de la parábola y evaluarla en los extremos, puedes determinar el precio que maximiza tus ingresos. ¡Es como encontrar el tesoro escondido en una búsqueda del tesoro!
Errores Comunes y Cómo Evitarlos
Al trabajar con el Teorema de Weierstrass, hay algunos errores comunes que debes evitar. Uno de ellos es no verificar la continuidad de la función. Recuerda, si la función no es continua, el teorema no se aplica. También es fácil olvidar que el intervalo debe ser cerrado y acotado. Si trabajas con intervalos abiertos, podrías perderte el máximo o mínimo que buscas.
Consejos Prácticos
Para evitar estos errores, siempre verifica la continuidad de tu función antes de aplicar el teorema. Haz una lista de los puntos críticos y evalúa la función en esos puntos, así como en los extremos del intervalo. ¡No dejes que la confusión te detenga!
El Teorema de Weierstrass es una herramienta poderosa que puede parecer complicada al principio, pero con práctica, se convierte en un aliado en tu viaje matemático. Desde funciones lineales hasta cuadráticas, el teorema garantiza que siempre haya un máximo y un mínimo en un intervalo cerrado y acotado. Así que la próxima vez que te enfrentes a una función, recuerda que siempre puedes contar con este teorema para guiarte.
- ¿Puedo aplicar el Teorema de Weierstrass a funciones discontinuas? No, el teorema se aplica únicamente a funciones continuas en intervalos cerrados y acotados.
- ¿Qué pasa si el intervalo es abierto? Si el intervalo es abierto, es posible que no se encuentren máximos o mínimos, ya que los extremos no están incluidos.
- ¿El teorema se aplica solo a funciones reales? Principalmente, sí, pero también se puede extender a funciones complejas bajo ciertas condiciones.
- ¿Cómo puedo saber si una función es continua? Puedes comprobar que no hay saltos, puntos de discontinuidad o asymptotas en el gráfico de la función.
- ¿Es necesario encontrar el vértice en funciones cuadráticas? No es necesario, pero es útil para determinar el máximo o mínimo en ese caso específico.
Este artículo proporciona una visión general y práctica del Teorema de Weierstrass, abordando ejemplos y aplicaciones para ayudar a los estudiantes a comprender mejor este concepto matemático fundamental.