¿Por qué es importante entender las funciones?
¡Hola! ¿Alguna vez te has sentido abrumado por las matemáticas? No te preocupes, no estás solo. Las funciones pueden parecer un laberinto complicado al principio, pero con un poco de práctica, pueden transformarse en un camino claro y directo. Las funciones son como recetas en un libro de cocina; cada una tiene sus propios ingredientes (valores de entrada) que, al mezclarse de la manera correcta, producen un platillo delicioso (valores de salida). Pero, ¿cómo puedes asegurarte de que estás siguiendo la receta correctamente? Aquí es donde entran los ejercicios de representación de funciones. Al practicar, no solo entenderás mejor cómo funcionan las funciones, sino que también te sentirás más seguro al abordarlas en exámenes o en situaciones cotidianas. Así que, ¡manos a la obra!
¿Qué es una función?
Antes de sumergirnos en los ejercicios, es fundamental que entendamos qué es una función. En términos simples, una función es una relación entre dos conjuntos de números, donde a cada elemento del primer conjunto (llamado dominio) le corresponde exactamente un elemento del segundo conjunto (llamado codominio). Imagina que tienes un saco de frutas y cada fruta tiene un número asignado. Si decides que a la manzana le corresponde el número 1, a la naranja el 2, y así sucesivamente, ¡has creado una función! Este es el primer paso para representar funciones y comprender su comportamiento.
Tipos de funciones
Funciones lineales
Las funciones lineales son como una línea recta que se extiende indefinidamente. Se representan en la forma y = mx + b, donde m es la pendiente y b es la intersección con el eje Y. Si piensas en una carretera que se extiende en línea recta, esa es la esencia de una función lineal. La pendiente indica qué tan empinada es la carretera; si m es positivo, la carretera sube; si es negativo, baja. ¿No es genial pensar en las funciones como caminos que podemos recorrer?
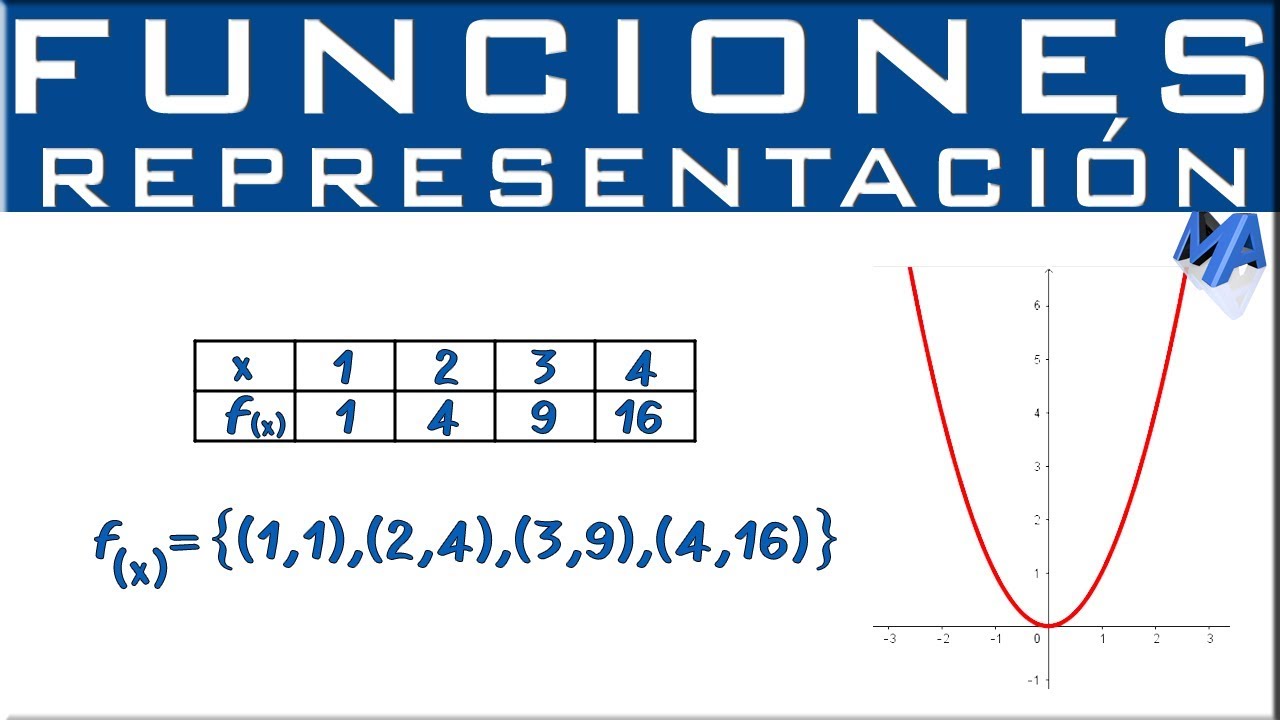
Funciones cuadráticas
Ahora, pasemos a las funciones cuadráticas. Estas son un poco más interesantes porque, en lugar de ser líneas rectas, forman una parábola. Se representan como y = ax² + bx + c. Imagina que lanzas una pelota al aire. Al principio, sube, pero luego, inevitablemente, cae. Esa trayectoria es similar a la de una función cuadrática. La forma de la parábola dependerá de los valores de a, b y c, así que jugar con estos números puede resultar en diferentes ‘lanzamientos’ de la pelota.
Ejercicios prácticos para representar funciones
Ahora que hemos cubierto lo básico, ¡es hora de practicar! La mejor manera de aprender es haciendo, así que aquí van algunos ejercicios que te ayudarán a mejorar tu comprensión.
Ejercicio 1: Graficar una función lineal
Elige la función y = 2x + 3. Comienza creando una tabla de valores. Elige algunos valores de x (por ejemplo, -2, -1, 0, 1, 2) y calcula el correspondiente valor de y. Luego, grafica estos puntos en un plano cartesiano. Une los puntos y observa cómo forman una línea recta. ¿Notaste cómo la pendiente (2) afecta la inclinación de la línea?
Ejercicio 2: Analizar una función cuadrática
Ahora, selecciona la función y = x² – 4. Al igual que antes, crea una tabla de valores, eligiendo valores de x que incluyan números negativos y positivos. Grafica los puntos y observa cómo forman una parábola. ¿Puedes identificar el vértice de la parábola? Es interesante ver cómo los cambios en los coeficientes afectan la forma de la gráfica, ¿verdad?
Interpretando las gráficas
Una vez que hayas graficado tus funciones, es crucial que aprendas a interpretar lo que ves. Cada gráfico cuenta una historia. La intersección con el eje Y te dice dónde comienza la función, y la pendiente o la forma de la parábola te muestra cómo se comporta la función a medida que te alejas del origen. Pregúntate: ¿qué sucede cuando x es grande? ¿Y cuando es pequeño? Esta curiosidad te ayudará a entender mejor el comportamiento de las funciones.
Consejos para mejorar en la representación de funciones
Practica con regularidad
La práctica hace al maestro. Cuanto más tiempo dediques a trabajar con funciones, más fácil será entenderlas. Intenta resolver diferentes tipos de problemas y no te limites a los ejemplos que ya conoces. Cuanto más variado sea tu enfoque, más preparado estarás para cualquier desafío que se presente.
Utiliza recursos en línea
Hay un mundo de recursos disponibles en línea. Desde videos hasta simuladores interactivos, estas herramientas pueden ofrecerte diferentes perspectivas y métodos de aprendizaje. A veces, escuchar a alguien más explicar un concepto puede hacer que todo haga clic en tu mente.
Formar grupos de estudio
Estudiar con otros puede ser muy beneficioso. Cada uno tiene su propio estilo de aprendizaje y al compartir ideas y resolver problemas juntos, pueden encontrar soluciones que tal vez no habrías considerado por tu cuenta. Además, ¡es más divertido aprender en compañía!
Entender y representar funciones puede parecer una tarea monumental, pero con práctica y dedicación, se convierte en un proceso mucho más manejable. Recuerda que cada función tiene su propia historia y, al aprender a leer esas historias, te conviertes en un mejor matemático. Así que sigue practicando, experimentando y explorando el fascinante mundo de las funciones. ¡Nunca se sabe qué maravillas matemáticas te esperan en el camino!
¿Cuál es la diferencia entre una función lineal y una cuadrática?
Las funciones lineales forman una línea recta y se representan como y = mx + b, mientras que las funciones cuadráticas forman una parábola y se representan como y = ax² + bx + c. La clave está en cómo los términos afectan la forma de la gráfica.
¿Cómo puedo saber si una relación es una función?
Una relación es una función si cada valor del dominio tiene exactamente un valor correspondiente en el codominio. Una manera rápida de verificarlo es usar la prueba de la línea vertical: si una línea vertical cruza la gráfica en más de un punto, no es una función.
¿Por qué es importante practicar la representación de funciones?
Practicar la representación de funciones te ayuda a comprender mejor cómo funcionan las matemáticas en el mundo real. Te prepara para resolver problemas más complejos y te da confianza en tus habilidades matemáticas.
Este artículo está diseñado para involucrar al lector y ayudar a que se sienta más cómodo con el concepto de funciones en matemáticas. Si necesitas más información o alguna modificación, ¡hazmelo saber!