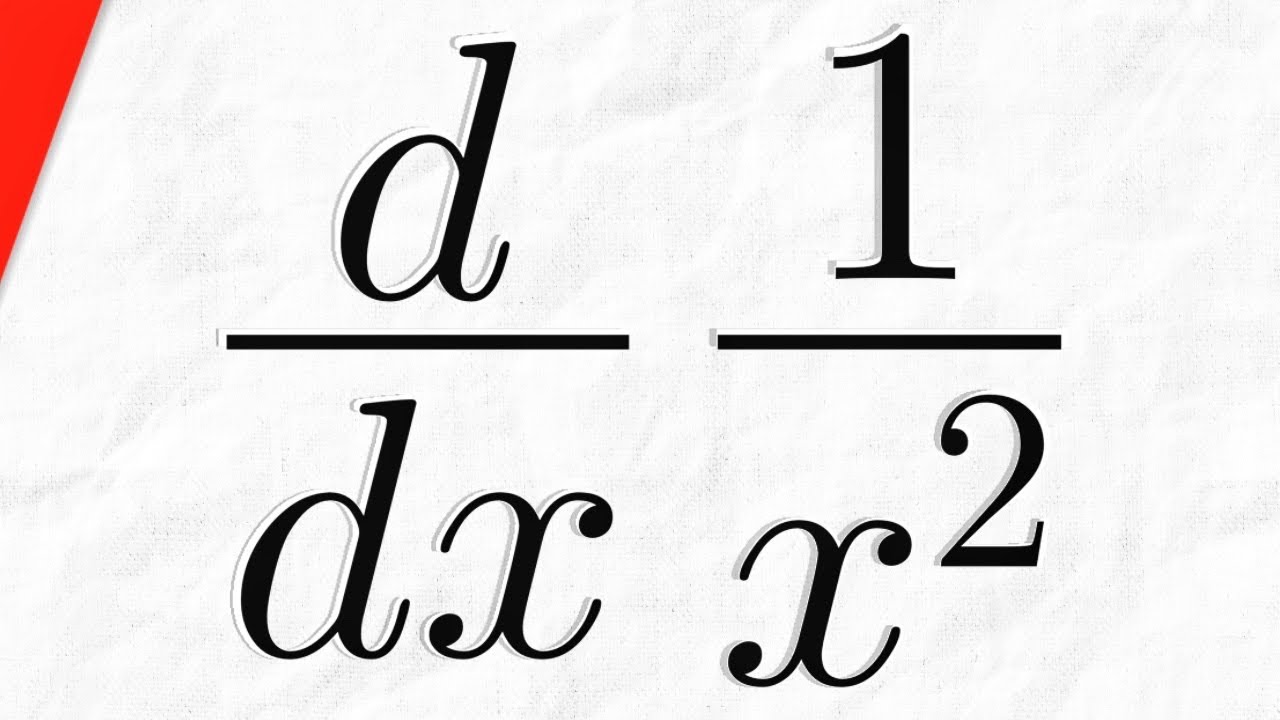¿Alguna vez te has preguntado cómo los matemáticos logran obtener esas respuestas tan rápidas y precisas? Bueno, hoy vamos a desmenuzar un tema que puede parecer complicado, pero que en realidad es bastante sencillo una vez que le agarras el truco: la derivada de la función 1/x². Así que, si estás listo para sumergirte en el mundo de las derivadas, ¡acomódate y empecemos!
### ¿Qué es una Derivada?
Antes de lanzarnos a calcular la derivada de 1/x², es crucial entender qué es una derivada. En términos simples, la derivada de una función mide cómo cambia esa función a medida que cambias la variable. Es como observar cómo se inclina una montaña: si subes, ¿qué tan rápido estás subiendo? La derivada te da esa respuesta.
### La Regla de Potencias
Para calcular la derivada de 1/x², primero debemos recordar que podemos reescribir esa función. En lugar de pensar en 1/x², podemos escribirlo como x^(-2). Esto nos permite aplicar la regla de potencias, que es una de las herramientas más útiles en el cálculo. La regla de potencias dice que si tienes una función en la forma f(x) = x^n, su derivada f'(x) es n*x^(n-1).
### Paso 1: Reescribir la Función
Así que, como mencionamos, 1/x² se convierte en x^(-2). Ahora estamos listos para aplicar la regla de potencias. Recuerda, esto es solo un cambio de perspectiva. En lugar de ver la función como fracciones, la estamos transformando en una forma que es más fácil de manejar.
### Paso 2: Aplicar la Regla de Potencias
Ahora que tenemos f(x) = x^(-2), aplicamos la regla de potencias. Aquí, n es -2. Así que, siguiendo la regla, la derivada se calcularía de la siguiente manera:
f'(x) = -2 * x^(-2 – 1)
Esto se convierte en:
f'(x) = -2 * x^(-3)
### Paso 3: Simplificar la Derivada
¡Estamos casi allí! Ahora, para hacer que nuestra respuesta sea más comprensible, podemos reescribir x^(-3) como 1/x³. Entonces, nuestra derivada final se verá así:
f'(x) = -2/x³
### ¿Por Qué es Importante?
Pero, ¿por qué deberías preocuparte por la derivada de 1/x²? Las derivadas son fundamentales en muchas áreas, como la física, la economía y la ingeniería. Nos ayudan a entender el comportamiento de funciones, optimizar problemas y modelar situaciones del mundo real. Por ejemplo, en física, la derivada puede ayudarte a entender cómo cambia la velocidad de un objeto con respecto al tiempo.
### Aplicaciones de la Derivada
#### Optimización
Imagina que eres un ingeniero que está diseñando un puente. Necesitas saber cómo cambiar la forma del puente afectará su resistencia. Las derivadas te permitirán optimizar el diseño para que sea seguro y eficiente.
#### Movimiento
Si estás en una carrera y quieres saber cómo tu velocidad cambia a lo largo del tiempo, la derivada de tu posición te dará esa información. Así, puedes ajustar tu ritmo para alcanzar la meta más rápidamente.
### Visualizando la Derivada
Ahora, para hacerlo aún más interesante, hablemos de cómo visualizar la derivada. Imagina que estás observando la gráfica de la función f(x) = 1/x². La curva tiene una forma particular, y la derivada te dice cómo se está inclinando en diferentes puntos. En los puntos donde la curva es más empinada, la derivada será más grande (en valor absoluto), y donde es más plana, la derivada será más pequeña.
### Ejemplo Práctico
Supongamos que quieres calcular la derivada de la función en un punto específico, digamos x = 1. Usando nuestra derivada f'(x) = -2/x³, simplemente sustituimos x = 1:
f'(1) = -2/(1)³ = -2
Esto significa que en x = 1, la pendiente de la tangente a la curva de f(x) = 1/x² es -2. En otras palabras, si dibujas una línea tangente en ese punto, se inclinará hacia abajo a una razón de 2 unidades verticales por cada 1 unidad horizontal.
### Resumen de Pasos
1. Reescribe la función como x^(-2).
2. Aplica la regla de potencias: f'(x) = -2 * x^(-3).
3. Simplifica: f'(x) = -2/x³.
### Conclusiones
Calcular la derivada de 1/x² no solo es un ejercicio matemático, sino que también abre la puerta a muchas aplicaciones en el mundo real. Desde la optimización en ingeniería hasta la comprensión de fenómenos físicos, las derivadas son herramientas esenciales en nuestra caja de herramientas matemática.
### Preguntas Frecuentes
#### ¿Puedo calcular la derivada de otras funciones similares?
¡Absolutamente! La misma técnica se puede aplicar a funciones como 1/x^n, donde n es cualquier número real. Solo recuerda reescribir la función en forma de potencia.
#### ¿Por qué la derivada de 1/x² es negativa?
La derivada es negativa porque la función 1/x² está decreciendo en todo su dominio. Esto significa que a medida que x aumenta, el valor de la función disminuye.
#### ¿Qué sucede con la derivada cuando x se acerca a cero?
La derivada se vuelve indefinida a medida que x se acerca a cero, ya que la función original tiene una asíntota vertical en x = 0. Esto significa que la función se dispara a infinito.
#### ¿Cómo se relaciona la derivada con la integral?
La derivada y la integral son operaciones inversas en cálculo. Mientras que la derivada mide el cambio, la integral suma esos cambios para encontrar el área bajo la curva.
¡Y ahí lo tienes! Ahora tienes las herramientas necesarias para calcular la derivada de 1/x² y entender su importancia en diversas aplicaciones. ¿Listo para practicar más? ¡Vamos a por ello!