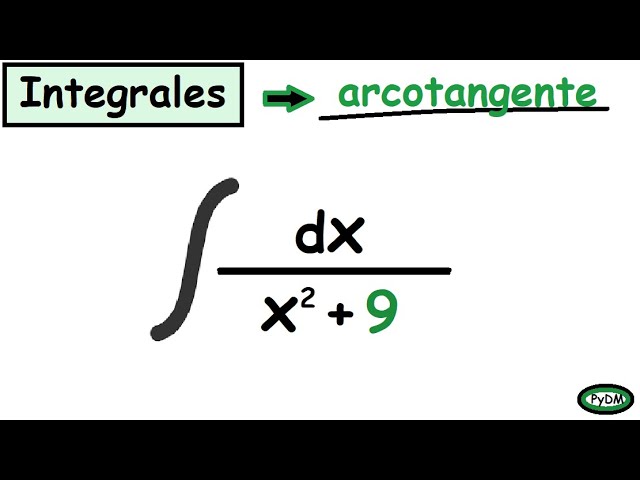¡Hola! Hoy vamos a sumergirnos en el fascinante mundo de las integrales de arcotangente. Tal vez te estés preguntando, «¿Qué es eso de la arcotangente y por qué debería importarme?» Bueno, la arcotangente es una función trigonométrica inversa que juega un papel crucial en el cálculo y, por ende, en muchas áreas de la ciencia y la ingeniería. Si alguna vez has sentido que las integrales son como un laberinto sin salida, no te preocupes, aquí estoy para guiarte. A lo largo de este artículo, desglosaremos las integrales de arcotangente, exploraremos métodos efectivos y te ofreceré ejemplos prácticos que te ayudarán a entender cómo funcionan. ¡Así que prepárate para convertirte en un experto en este tema!
¿Qué es la Arcotangente?
La arcotangente, denotada como arctan(x) o tan-1(x), es la función inversa de la tangente. Es decir, si y = tan(x), entonces x = arctan(y). Esta función nos ayuda a encontrar el ángulo cuyo tangente es un número dado. En términos más simples, si tienes un triángulo rectángulo y conoces la longitud de los lados opuestos y adyacentes, puedes usar la arcotangente para calcular el ángulo. ¡Es como tener una brújula que te señala la dirección correcta en un mar de números!
¿Por qué estudiar las integrales de arcotangente?
Tal vez te preguntes, «¿Qué utilidad tienen las integrales de arcotangente en la vida real?» La respuesta es: ¡mucho! Estas integrales aparecen en diversas aplicaciones, desde la física hasta la ingeniería. Por ejemplo, al resolver problemas relacionados con la velocidad, el movimiento y las ondas, las integrales de arcotangente pueden ser tu mejor aliada. Además, entender cómo funcionan te dará una base sólida para abordar otros conceptos más avanzados en cálculo. Es como construir una casa: necesitas una buena base antes de poder levantar las paredes.
Métodos para Calcular la Integral de Arcotangente
Integración por Sustitución
Uno de los métodos más comunes para calcular la integral de arcotangente es a través de la integración por sustitución. Imagina que tienes la integral de la forma:
∫ (1/(1+x²)) dxSabemos que la derivada de arctan(x) es 1/(1+x²). Así que, al integrar, simplemente obtendremos:
arctan(x) + CDonde C es la constante de integración. Este es un caso simple, pero sirve para ilustrar cómo funciona la sustitución. La clave aquí es reconocer las funciones y sus derivadas. ¿Te suena familiar?
Integración por Partes
Otro método útil es la integración por partes, que se basa en la fórmula:
∫ u dv = uv - ∫ v duDigamos que queremos calcular:
∫ x/(1+x²) dxPodemos elegir u = x y dv = (1/(1+x²)) dx. Al aplicar la fórmula, obtenemos:
uv - ∫ v du = (x * arctan(x)) - ∫ (arctan(x)) dxEste método puede parecer un poco más complicado, pero es extremadamente poderoso. Recuerda, la práctica hace al maestro, así que no te desanimes si no lo entiendes a la primera.
Uso de Tablas de Integrales
Si prefieres un enfoque más directo, las tablas de integrales son una herramienta valiosa. Muchas veces, no necesitas reinventar la rueda. En las tablas, encontrarás la integral de arcotangente ya resuelta, lo que te ahorrará tiempo y esfuerzo. Por ejemplo:
∫ arctan(x) dx = x * arctan(x) - (1/2) * ln(1+x²) + CEste es un gran recurso para aquellos días en que simplemente no tienes ganas de trabajar demasiado. ¡A veces, hay que ser astuto!
Ejemplos Prácticos de Integrales de Arcotangente
Ejemplo 1: Integral Directa
Vamos a resolver la integral:
∫ (1/(1+x²)) dx
Como mencionamos anteriormente, sabemos que:
∫ (1/(1+x²)) dx = arctan(x) + CAsí que, ¡ya tenemos la respuesta! Este es un ejemplo sencillo, pero fundamental. A medida que avanzamos, verás cómo las cosas se complican un poco más.
Ejemplo 2: Integral con Sustitución
Ahora, veamos un caso más interesante:
∫ (2x/(1+x²)) dxEn este caso, podemos usar la sustitución. Tomemos u = 1 + x², lo que implica que du = 2x dx. Así que la integral se convierte en:
∫ (1/u) du = ln|u| + C = ln|1+x²| + C¡Y ahí lo tienes! Un ejemplo donde la sustitución hace que la integral sea mucho más manejable.
Ejemplo 3: Integral por Partes
Finalmente, veamos un ejemplo que involucra la integración por partes:
∫ x * arctan(x) dxUsando la fórmula de integración por partes, eligiendo u = arctan(x) y dv = x dx, obtenemos:
uv - ∫ v du = x * arctan(x) - ∫ (x/(1+x²)) dxResolviendo la integral restante, llegamos a:
x * arctan(x) - (1/2) * ln(1+x²) + CEste ejemplo muestra cómo las integrales pueden complicarse, pero con las herramientas adecuadas, ¡todo es posible!
En resumen, las integrales de arcotangente son un tema apasionante que no solo tiene aplicaciones prácticas, sino que también puede ser divertido de aprender. Desde la integración por sustitución hasta la integración por partes, hemos cubierto diferentes métodos que te ayudarán a abordar este tipo de integrales con confianza. Recuerda, la clave es practicar y no rendirte. Así que, ¿qué te parece si intentas resolver algunas integrales por tu cuenta? ¡Te prometo que vale la pena!
¿Las integrales de arcotangente tienen aplicaciones en la vida real?
¡Definitivamente! Se utilizan en física, ingeniería y en problemas relacionados con la velocidad y el movimiento, entre otros.
¿Es necesario conocer la derivada de la arcotangente para resolver integrales?
Conocer la derivada es muy útil, ya que muchas integrales de arcotangente se basan en esa relación. Es como tener un mapa que te guía por el camino correcto.
¿Qué herramientas puedo usar para practicar integrales de arcotangente?
Las tablas de integrales, calculadoras y software de matemáticas son excelentes recursos. Además, no subestimes el poder de los libros de texto y las plataformas en línea.
¿Qué consejo me darías para mejorar en integrales de arcotangente?
Practica regularmente y no temas cometer errores. Cada error es una oportunidad para aprender y mejorar tus habilidades matemáticas.
Espero que este artículo sea útil y te ayude a comprender mejor las integrales de arcotangente. ¡No dudes en preguntar si tienes más dudas!