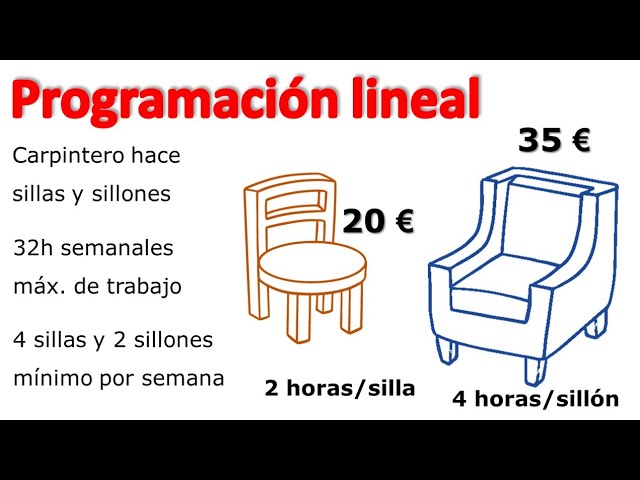
La programación lineal es una técnica poderosa en el campo de la optimización, utilizada para maximizar o minimizar una función objetivo sujeta a ciertas restricciones. Pero, ¿alguna vez te has encontrado con problemas que parecen insuperables al trabajar en este ámbito? No te preocupes, no estás solo. En este artículo, vamos a explorar los 10 problemas más comunes que enfrentan los programadores lineales y cómo puedes solucionarlos. Así que, si estás listo para convertirte en un maestro de la programación lineal, ¡sigue leyendo!
Entender la Función Objetivo
Uno de los errores más frecuentes al abordar la programación lineal es la confusión sobre la función objetivo. ¿Qué es exactamente? La función objetivo es la expresión matemática que queremos maximizar o minimizar. A menudo, los principiantes luchan por definirla claramente. La clave aquí es formularla de manera sencilla. ¿Estás buscando maximizar ganancias o minimizar costos? Define tu objetivo en términos claros y concisos.
Solución
Para aclarar tu función objetivo, intenta descomponerla. Pregúntate: ¿Cuáles son las variables que afectan mi objetivo? Al identificar estos elementos, podrás formular una función más efectiva. No dudes en utilizar diagramas o gráficos para visualizar mejor tu problema. ¡A veces, ver es creer!
Definir las Restricciones
Otro obstáculo común es la definición de restricciones. Estas son las limitaciones que deben ser respetadas en el modelo. Muchos principiantes simplemente se olvidan de incluir restricciones o las plantean de forma incorrecta. ¿Por qué es esto un problema? Porque si tus restricciones no reflejan la realidad, tu solución será inútil.
Solución
Tómate un tiempo para pensar en las limitaciones reales de tu problema. ¿Tienes un presupuesto que no puedes exceder? ¿Hay recursos limitados? Escribe todas tus restricciones de forma clara y asegúrate de que sean coherentes con la función objetivo. Recuerda que una buena restricción es como una buena receta: necesita los ingredientes correctos.
Manejo de Variables No Negativas
En programación lineal, las variables a menudo deben ser no negativas. Esto significa que no puedes tener cantidades negativas de algo, como productos o recursos. Sin embargo, es común que los programadores olviden esta regla y terminen con soluciones que no tienen sentido. ¿Te imaginas tener -5 manzanas? ¡No suena bien!
Solución
Siempre que estés planteando tu modelo, recuerda incluir la condición de no negatividad. Puedes hacerlo simplemente añadiendo la restricción ( x geq 0 ) para cada variable. Esto garantizará que tus soluciones sean viables y realistas.
Elegir el Método Correcto
Hay varios métodos para resolver problemas de programación lineal, como el método gráfico, el método simplex y otros algoritmos más avanzados. Pero, ¿cómo sabes cuál elegir? Esta decisión puede ser un verdadero dolor de cabeza. Algunos métodos son más adecuados para problemas simples, mientras que otros son mejores para problemas más complejos.
Solución
Para elegir el método correcto, evalúa la complejidad de tu problema. Si estás lidiando con un problema sencillo con dos variables, el método gráfico puede ser suficiente. Sin embargo, si tienes muchas variables y restricciones, el método simplex o software especializado como LINDO o MATLAB podría ser la solución. No tengas miedo de experimentar y ver qué funciona mejor para ti.
Interpretar Resultados
Una vez que has resuelto tu problema, es hora de interpretar los resultados. Este paso es crucial, pero a menudo se pasa por alto. ¿Qué significan realmente esos números? A veces, los resultados pueden ser confusos o parecer no tener sentido. ¿Te ha pasado alguna vez?
Solución
Para interpretar correctamente tus resultados, vuelve a la función objetivo y a las restricciones. Pregúntate: ¿Los resultados cumplen con mis restricciones? ¿Tienen sentido en el contexto de mi problema? Si algo no cuadra, es posible que debas revisar tu modelo y asegurarte de que todo esté correctamente formulado.
Dificultades con Problemas de Múltiples Soluciones
A veces, puedes encontrarte con un problema que tiene múltiples soluciones óptimas. Esto puede ser desconcertante, especialmente si no estás preparado para manejarlo. ¿Qué haces cuando hay más de una respuesta correcta? ¿Significa eso que has cometido un error?
Solución
No te preocupes, tener múltiples soluciones óptimas no es un error. Es una característica de ciertos problemas de programación lineal. Si te enfrentas a esta situación, considera las implicaciones de cada solución y elige la que mejor se adapte a tus necesidades. También puedes optar por un enfoque de optimización adicional, como minimizar costos o maximizar beneficios, para decidir cuál solución es la más adecuada.
Falta de Sensibilidad y Análisis de Escenarios
Otro problema común es no realizar un análisis de sensibilidad. ¿Sabías que los cambios en las restricciones o en los coeficientes de la función objetivo pueden afectar drásticamente tus resultados? Ignorar este aspecto puede llevarte a decisiones equivocadas. ¿Te imaginas tomar una decisión basada en datos que podrían cambiar?
Solución
Realiza un análisis de sensibilidad para comprender cómo los cambios en tu modelo pueden afectar los resultados. Pregúntate: ¿Qué pasaría si mi presupuesto se reduce? ¿O si el costo de un recurso aumenta? Esto te permitirá tomar decisiones más informadas y prepararte para posibles escenarios futuros.
Errores en la Codificación
Si estás utilizando software para resolver tu problema de programación lineal, los errores de codificación pueden ser un gran obstáculo. Un pequeño error tipográfico puede llevar a resultados completamente incorrectos. ¿Te ha pasado? Es frustrante, ¿verdad?
Solución
Para evitar errores de codificación, siempre revisa tu modelo y asegúrate de que todas las variables y restricciones estén correctamente ingresadas. Puedes hacer una revisión cruzada con un compañero o utilizar herramientas de depuración para identificar posibles problemas en tu código. ¡Un par de ojos adicionales nunca está de más!
No Validar el Modelo
Finalmente, uno de los errores más grandes que puedes cometer es no validar tu modelo. Después de todo el trabajo que has puesto, ¿cómo puedes estar seguro de que tu solución es correcta? Sin una validación adecuada, podrías estar tomando decisiones basadas en información errónea.
Solución
Valida tu modelo comparando los resultados con datos reales o utilizando un conjunto de pruebas. Pregúntate: ¿Los resultados son razonables? ¿Se alinean con la realidad? Si algo no parece correcto, vuelve a revisar tu modelo y ajusta según sea necesario. La validación es como un cinturón de seguridad; nunca sabes cuándo lo vas a necesitar.
Ignorar el Aprendizaje Continuo
Finalmente, no olvides que la programación lineal es un campo en constante evolución. Ignorar la necesidad de aprender y adaptarse puede dejarte atrás. ¿Te gustaría quedarte estancado mientras el mundo avanza a tu alrededor?
Solución
Dedica tiempo a aprender nuevas técnicas y herramientas. Participa en foros, asiste a talleres o sigue cursos en línea. Mantente al tanto de las últimas tendencias y avances en programación lineal. Recuerda, la práctica hace al maestro, y siempre hay algo nuevo que aprender.
La programación lineal puede ser un desafío, pero también es una herramienta increíblemente útil. Al conocer y abordar estos problemas comunes, estarás mejor preparado para enfrentarte a cualquier reto que se presente. Así que la próxima vez que te encuentres con un obstáculo, recuerda estos consejos y sigue adelante. ¡La solución está al alcance de tu mano!
¿Qué es la programación lineal?
La programación lineal es un método matemático para optimizar una función objetivo sujeta a restricciones lineales. Se utiliza en diversos campos, como la economía, la ingeniería y la logística.
¿Cuáles son los métodos más comunes para resolver problemas de programación lineal?
Los métodos más comunes son el método gráfico, el método simplex y el uso de software especializado como LINDO, MATLAB o Python con bibliotecas como PuLP o SciPy.
¿Qué debo hacer si mi modelo tiene múltiples soluciones óptimas?
Evalúa las diferentes soluciones y elige la que mejor se adapte a tus necesidades. Considera factores como costos, tiempo y recursos disponibles para tomar una decisión informada.
¿Cómo puedo validar mi modelo de programación lineal?
Valida tu modelo comparando los resultados con datos reales o utilizando un conjunto de pruebas. Asegúrate de que los resultados sean razonables y se alineen con la realidad.
¿Es importante el análisis de sensibilidad en programación lineal?
Sí, el análisis de sensibilidad es crucial, ya que te permite entender cómo los cambios en las restricciones o en los coeficientes de la función objetivo pueden afectar tus resultados. Esto te ayuda a tomar decisiones más informadas.
Espero que este artículo sea útil y cumpla con tus expectativas. Si tienes alguna pregunta o necesitas más información, no dudes en preguntar. ¡Feliz programación!