Los sistemas de ecuaciones son una parte fundamental de las matemáticas, especialmente en el álgebra. Pero, ¿qué son exactamente? Imagina que tienes varias incógnitas que deseas resolver al mismo tiempo, como si fueras un detective tratando de juntar las pistas para resolver un misterio. Cada ecuación en el sistema es una pista que te acerca más a la solución. En este artículo, exploraremos los diferentes tipos de sistemas de ecuaciones, ejemplos prácticos y cómo podemos resolverlos. ¡Así que ponte cómodo y prepárate para sumergirte en el fascinante mundo de las ecuaciones!
¿Qué es un Sistema de Ecuaciones?
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que comparten al menos una variable. La solución de este sistema es el conjunto de valores que satisfacen todas las ecuaciones simultáneamente. Por ejemplo, si tienes dos ecuaciones, la solución sería el punto donde ambas líneas se cruzan en un gráfico. Pero no todos los sistemas son iguales; aquí es donde entra la clasificación.
Tipos de Sistemas de Ecuaciones
Sistemas Compatibles
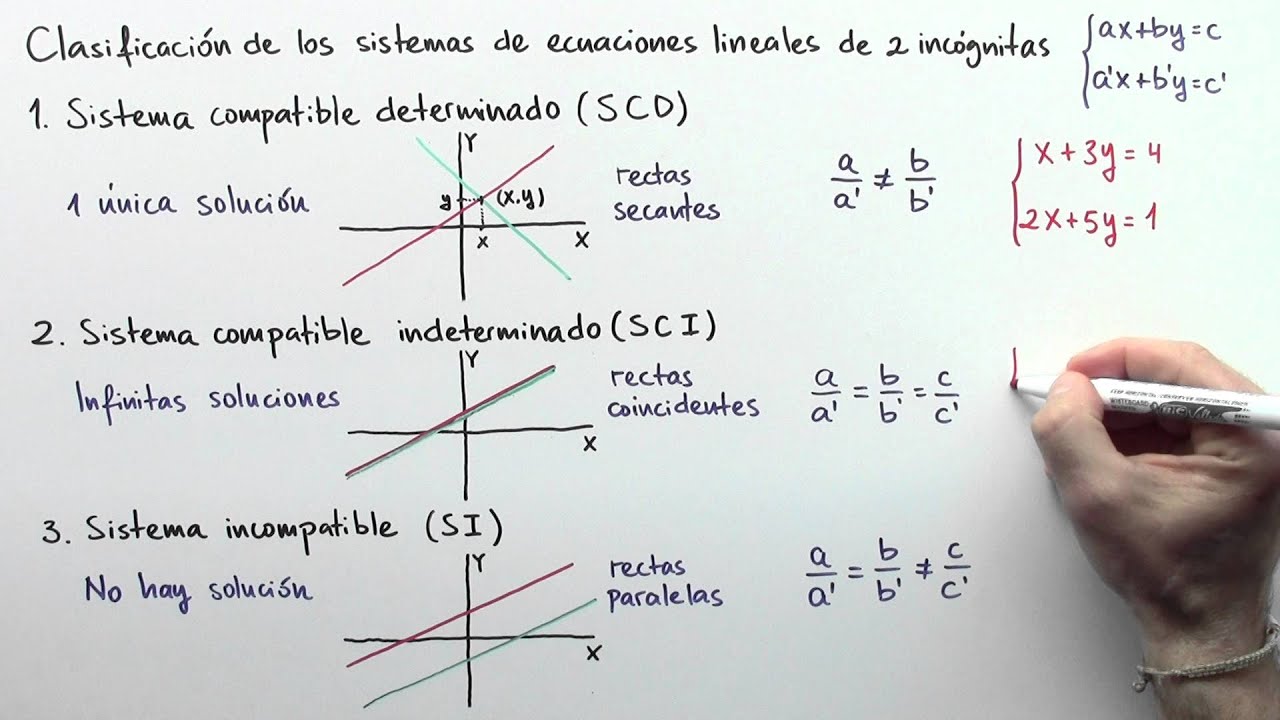
Los sistemas compatibles son aquellos que tienen al menos una solución. Dentro de esta categoría, podemos encontrar:
- Sistemas Compatibles Determinados: Tienen exactamente una solución. Piensa en un cruce de caminos: hay un único camino que debes tomar. Por ejemplo, el sistema de ecuaciones:
- 2x + 3y = 6
- x – y = 2
- Sistemas Compatibles Indeterminados: Tienen infinitas soluciones. Es como un río que se bifurca en múltiples caminos: hay muchas maneras de llegar a un destino. Por ejemplo:
- 2x + 4y = 8
- x + 2y = 4
Este sistema tiene un único punto donde se cruzan ambas líneas.
Ambas ecuaciones representan la misma línea en el gráfico, lo que significa que hay infinitas combinaciones de x e y que satisfacen el sistema.
Sistemas Incompatibles
Los sistemas incompatibles, por otro lado, no tienen solución. Imagina que intentas encontrar un lugar donde dos caminos paralelos se crucen; eso es imposible. Un ejemplo sería:
- 2x + 3y = 6
- 2x + 3y = 10
Aquí, ambas ecuaciones representan líneas paralelas que nunca se encuentran. Por lo tanto, no hay solución posible.
Ejemplos Prácticos
Ejemplo de un Sistema Compatible Determinado
Vamos a resolver el siguiente sistema:
- 2x + 3y = 6
- x – y = 2
Podemos resolverlo utilizando el método de sustitución. Primero, despejamos x en la segunda ecuación:
x = y + 2
Ahora, sustituimos x en la primera ecuación:
2(y + 2) + 3y = 6
Esto se simplifica a:
2y + 4 + 3y = 6
5y + 4 = 6
5y = 2
y = 0.4
Ahora sustituimos y en la ecuación de x:
x = 0.4 + 2 = 2.4
Así que la solución del sistema es (2.4, 0.4).
Ejemplo de un Sistema Compatible Indeterminado
Ahora, veamos un sistema compatible indeterminado:
- 2x + 4y = 8
- x + 2y = 4
Si resolvemos la segunda ecuación para x, obtenemos:
x = 4 – 2y
Ahora, sustituimos x en la primera ecuación:
2(4 – 2y) + 4y = 8
Esto se simplifica a:
8 – 4y + 4y = 8
Lo que es cierto para cualquier valor de y. Esto significa que hay infinitas soluciones.
Ejemplo de un Sistema Incompatible
Finalmente, veamos un sistema incompatible:
- 2x + 3y = 6
- 2x + 3y = 10
Si intentamos resolver estas ecuaciones, notaremos que no hay forma de que ambas sean verdaderas al mismo tiempo. Esto es porque representan líneas paralelas. No hay solución.
Métodos de Resolución de Sistemas de Ecuaciones
Método de Sustitución
El método de sustitución es como un juego de «encuentra la pareja». Primero, despejas una variable en una ecuación y luego sustituyes ese valor en la otra ecuación. Este método es muy útil cuando una de las ecuaciones ya está despejada o se puede despejar fácilmente.
Método de Igualación
Este método implica igualar las dos expresiones de la misma variable. Es como si tuvieras dos recetas diferentes para el mismo platillo y decides combinarlas. Una vez que igualas, puedes resolver para una variable y luego sustituir en cualquiera de las ecuaciones originales.
Método de Eliminación
El método de eliminación es como limpiar un desorden: eliminas una de las variables sumando o restando las ecuaciones. Por ejemplo, si tienes:
- 2x + 3y = 6
- 4x + 6y = 12
Si multiplicas la primera ecuación por 2, verás que ambas ecuaciones son equivalentes. Al restar, puedes eliminar una variable.
Aplicaciones de los Sistemas de Ecuaciones
Los sistemas de ecuaciones tienen aplicaciones en diversas áreas, como la economía, la ingeniería y las ciencias sociales. Por ejemplo, en economía, se pueden usar para encontrar el equilibrio en un mercado. En ingeniería, ayudan a resolver problemas relacionados con circuitos eléctricos. Las posibilidades son infinitas, y eso es lo que los hace tan fascinantes.
¿Qué es un sistema de ecuaciones lineales?
Un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones lineales que involucran las mismas variables. Su objetivo es encontrar los valores de esas variables que satisfacen todas las ecuaciones al mismo tiempo.
¿Cuántas soluciones puede tener un sistema de ecuaciones?
Un sistema puede tener una solución (compatible determinado), infinitas soluciones (compatible indeterminado) o ninguna solución (incompatible).
¿Cuál es el método más fácil para resolver sistemas de ecuaciones?
El método más fácil depende de la situación. Si una ecuación ya está despejada, el método de sustitución puede ser el más sencillo. Si las ecuaciones son simples, el método de eliminación puede ser más rápido.
¿Dónde se utilizan los sistemas de ecuaciones en la vida real?
Se utilizan en diversas áreas, incluyendo la economía, la ingeniería, la física y las ciencias sociales, para modelar situaciones donde múltiples factores interactúan entre sí.
¿Puedo resolver un sistema de ecuaciones gráficamente?
Sí, puedes graficar las ecuaciones en un plano cartesiano. El punto de intersección de las líneas representará la solución del sistema.
Espero que este artículo cumpla con tus expectativas y te ayude a comprender mejor los sistemas de ecuaciones. Si tienes más preguntas o necesitas más ejemplos, ¡no dudes en preguntar!