¿Alguna vez te has encontrado con una función que parece un rompecabezas? Las funciones irracionales son precisamente eso: un reto fascinante que puede ser complicado al principio, pero que se vuelve más claro con la práctica. En este artículo, nos sumergiremos en el mundo de las funciones irracionales, explorando su naturaleza, cómo funcionan y, lo más importante, cómo puedes dominarlas a través de ejercicios prácticos. Así que, si estás listo para mejorar tu comprensión matemática, sigue leyendo y prepárate para desentrañar los misterios de estas funciones.
¿Qué Son las Funciones Irracionales?
Primero, aclaremos qué entendemos por funciones irracionales. En términos sencillos, una función irracional es aquella que incluye raíces cuadradas, cúbicas o de grados superiores de variables. Por ejemplo, la función f(x) = √x o g(x) = 3√(x-2) son ejemplos típicos. La clave aquí es que la variable está dentro de una raíz, lo que hace que la función no se pueda expresar como un polinomio. Esto puede parecer intimidante, pero una vez que comprendes su estructura, se convierte en un juego.
Características de las Funciones Irracionales
Las funciones irracionales tienen características únicas que las diferencian de las funciones racionales. Por ejemplo, a menudo no están definidas para ciertos valores de x. En el caso de f(x) = √x, no puedes sustituir valores negativos porque no hay una raíz cuadrada real de un número negativo. ¿Ves cómo esto puede llevar a situaciones inesperadas? Además, el dominio de estas funciones suele ser más restringido. Es como si estuvieras jugando un videojuego donde solo puedes entrar a ciertas áreas; necesitas saber dónde puedes y no puedes ir.
Dominio y Rango de Funciones Irracionales
El dominio de una función es el conjunto de valores de x para los cuales la función está definida. Por otro lado, el rango es el conjunto de valores que puede tomar la función. Para nuestras funciones irracionales, determinar el dominio es esencial. Por ejemplo, en f(x) = √(x – 1), el dominio se limita a x ≥ 1. Si intentas introducir un valor menor que 1, te enfrentarás a un número imaginario, lo que no es el objetivo aquí.
Ejemplo Práctico: Encontrando el Dominio
Imagina que tienes la función h(x) = √(2x + 3). Para encontrar el dominio, necesitas asegurarte de que el argumento de la raíz sea mayor o igual a cero. Así que, resolviendo 2x + 3 ≥ 0, llegamos a x ≥ -3. Por lo tanto, el dominio de h(x) es [-3, ∞). ¿Fácil, verdad? Ahora ya tienes una herramienta para trabajar con funciones irracionales.
Graficando Funciones Irracionales
Una vez que comprendes el dominio, es hora de graficar. Graficar funciones irracionales puede ser sorprendentemente gratificante. Te permite visualizar cómo se comportan estas funciones en diferentes intervalos. Por ejemplo, la gráfica de f(x) = √x comienza en el origen (0,0) y se extiende hacia la derecha, nunca tocando el eje x negativo. Esto ilustra perfectamente cómo el dominio restringido afecta la gráfica.
Pasos para Graficar una Función Irracional
- Determina el dominio de la función.
- Elige algunos valores de x dentro del dominio y calcula los valores correspondientes de f(x).
- Plotea los puntos en un sistema de coordenadas.
- Une los puntos con una línea suave, teniendo en cuenta que la función no se extiende a valores fuera del dominio.
¿Ves cómo la gráfica se convierte en un mapa que te ayuda a entender mejor la función? Es como tener una brújula en medio de un bosque; te guía y te muestra el camino correcto.
Ejercicios Prácticos para Mejorar tus Habilidades
Ahora que hemos cubierto los conceptos básicos, es hora de poner manos a la obra. Aquí hay algunos ejercicios prácticos que te ayudarán a afianzar tus conocimientos sobre funciones irracionales.
Ejercicio 1: Encuentra el Dominio
Determina el dominio de la función f(x) = √(x^2 – 4). Recuerda que el argumento de la raíz debe ser mayor o igual a cero. ¿Puedes hacerlo?
Ejercicio 2: Graficando Funciones
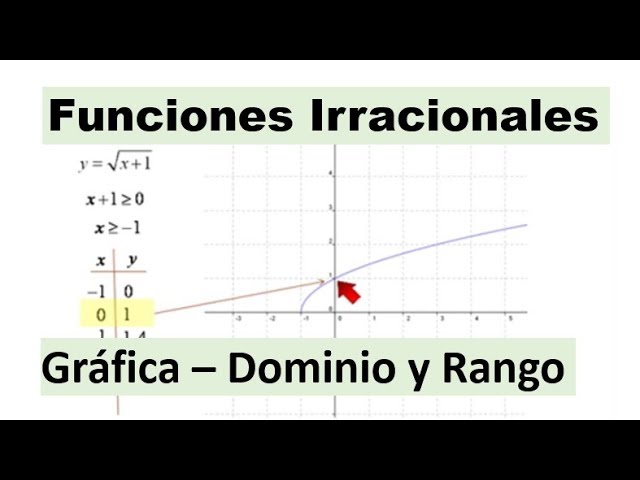
Graficar la función g(x) = √(x + 1). Sigue los pasos que discutimos anteriormente y observa cómo se comporta la función. ¿Qué observas sobre su forma y su dominio?
Ejercicio 3: Composición de Funciones
Si tienes dos funciones, f(x) = √(x) y g(x) = x^2, intenta encontrar la composición (f o g)(x) = f(g(x)). ¿Qué resultado obtienes? Esto es esencial para entender cómo se relacionan las funciones entre sí.
Aplicaciones de las Funciones Irracionales
Las funciones irracionales no solo son un ejercicio académico; tienen aplicaciones en el mundo real. Por ejemplo, en física, las ecuaciones que involucran raíces pueden describir la trayectoria de un objeto en caída libre. En la economía, algunas funciones irracionales se utilizan para modelar costos y beneficios. Así que, aunque puedas pensar que estas funciones son solo un concepto abstracto, en realidad, son herramientas poderosas que te ayudarán a resolver problemas del mundo real.
Ejemplo del Mundo Real
Imagina que estás diseñando un parque y necesitas calcular la longitud de una rampa. Si la rampa se eleva 3 metros y se extiende 4 metros horizontalmente, puedes usar la fórmula de la distancia en un triángulo rectángulo: d = √(3^2 + 4^2). Aquí, estás aplicando una función irracional para encontrar la solución a un problema práctico. ¿No es genial cómo las matemáticas se entrelazan con nuestra vida diaria?
Consejos para Dominar las Funciones Irracionales
Si quieres ser un experto en funciones irracionales, aquí tienes algunos consejos prácticos:
- Practica Regularmente: La práctica hace al maestro. Cuanto más trabajes con funciones irracionales, más cómodo te sentirás.
- Utiliza Recursos Visuales: Las gráficas son tus amigas. Visualizar funciones te ayudará a comprender mejor su comportamiento.
- No Temas Preguntar: Si te atascas, no dudes en pedir ayuda. Las matemáticas pueden ser complicadas, y es normal necesitar un empujón.
Las funciones irracionales pueden parecer desafiantes al principio, pero con la práctica y los ejercicios adecuados, puedes dominarlas y utilizarlas en situaciones del mundo real. Así que, la próxima vez que te encuentres con una función irracional, recuerda que tienes las herramientas y el conocimiento para enfrentarla. ¿Listo para el desafío? ¡Vamos a hacerlo!
¿Cuál es la diferencia entre una función racional e irracional?
Las funciones racionales pueden expresarse como una fracción de polinomios, mientras que las funciones irracionales incluyen raíces que no se pueden simplificar a un polinomio.
¿Cómo se resuelven ecuaciones que involucran funciones irracionales?
Para resolver ecuaciones con funciones irracionales, a menudo necesitas elevar al cuadrado ambos lados de la ecuación para eliminar la raíz, pero debes tener cuidado con las soluciones extraviadas.
¿Pueden las funciones irracionales tener un rango negativo?
No, la mayoría de las funciones irracionales que involucran raíces cuadradas tienen un rango que comienza en cero y se extiende hacia el infinito, ya que no puedes obtener un valor negativo al tomar la raíz cuadrada de un número real.