¿Alguna vez te has preguntado cómo se pueden combinar dos matrices para obtener una nueva? La multiplicación de matrices es una herramienta poderosa en matemáticas y tiene aplicaciones en diversos campos, desde la física hasta la informática. En este artículo, te llevaré a través de un viaje sencillo y práctico sobre cómo multiplicar matrices 2×2. Así que, si estás listo para sumergirte en el fascinante mundo de las matrices, ¡comencemos!
¿Qué es una Matriz?
Antes de entrar en la multiplicación, hablemos un poco sobre qué es una matriz. Imagina que tienes una tabla con filas y columnas; eso es una matriz. Por ejemplo, una matriz 2×2 tiene dos filas y dos columnas. Su forma general se ve así:
| a b | | c d |
Donde a, b, c y d son números que llamamos elementos de la matriz. ¡Sencillo, ¿verdad? Ahora que sabemos qué es una matriz, vamos a aprender cómo multiplicarlas!
Cómo Multiplicar Matrices 2×2
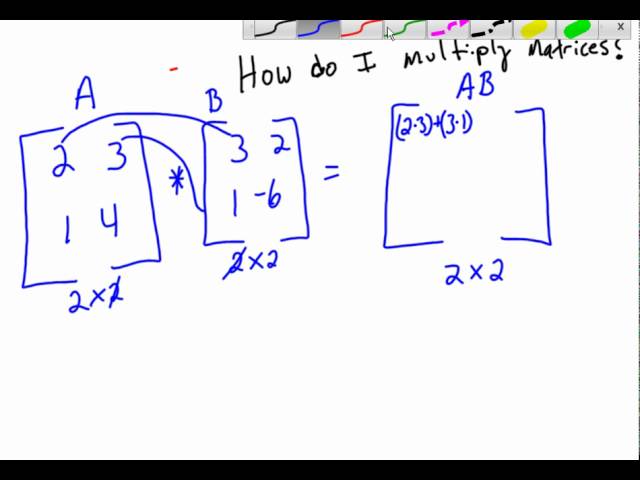
Multiplicar matrices puede parecer complicado al principio, pero con un poco de práctica, se vuelve pan comido. Para multiplicar dos matrices 2×2, seguimos un método específico. Supongamos que tenemos las siguientes dos matrices:
Matriz A: | a b | | c d | Matriz B: | e f | | g h |
El resultado de la multiplicación de A y B, que llamaremos Matriz C, se verá así:
Matriz C: | i j | | k l |
Donde los elementos de la Matriz C se calculan de la siguiente manera:
- i = a * e + b * g
- j = a * f + b * h
- k = c * e + d * g
- l = c * f + d * h
Así que, si tenemos los números específicos, podemos calcular cada uno de estos elementos. Vamos a verlo con un ejemplo práctico.
Ejemplo Práctico de Multiplicación de Matrices
Supongamos que tenemos las siguientes matrices:
Matriz A: | 1 2 | | 3 4 | Matriz B: | 5 6 | | 7 8 |
Ahora, multipliquemos A por B siguiendo las fórmulas que mencionamos antes:
- i = 1 * 5 + 2 * 7 = 5 + 14 = 19
- j = 1 * 6 + 2 * 8 = 6 + 16 = 22
- k = 3 * 5 + 4 * 7 = 15 + 28 = 43
- l = 3 * 6 + 4 * 8 = 18 + 32 = 50
Por lo tanto, nuestra Matriz C se verá así:
Matriz C: | 19 22 | | 43 50 |
¿Por Qué es Importante la Multiplicación de Matrices?
La multiplicación de matrices no es solo un ejercicio matemático; tiene un montón de aplicaciones prácticas. Desde gráficos por computadora hasta resolver sistemas de ecuaciones lineales, entender cómo multiplicar matrices te abre las puertas a un mundo lleno de posibilidades. ¿Alguna vez has jugado un videojuego? Detrás de la pantalla, hay un montón de cálculos con matrices que hacen que todo funcione sin problemas. ¡Increíble, ¿verdad?
Propiedades de la Multiplicación de Matrices
Ahora que ya sabes cómo multiplicar matrices, es útil conocer algunas propiedades de esta operación. Estas propiedades pueden hacerte la vida más fácil cuando trabajas con matrices. Aquí hay algunas de ellas:
- No conmutativa: A * B no es lo mismo que B * A. ¡Sorpresa! El orden importa.
- Asociativa: (A * B) * C = A * (B * C). Puedes agrupar las matrices como quieras.
- Distributiva: A * (B + C) = A * B + A * C. Puedes distribuir la multiplicación sobre la suma.
Estas propiedades son como las reglas del juego. Te ayudan a navegar por el mundo de las matrices sin perderte.
Ejercicios Prácticos para Reforzar el Aprendizaje
La mejor manera de aprender es practicando. Aquí tienes algunos ejercicios que puedes intentar:
- Multiplica las siguientes matrices:
Matriz A:
| 2 3 |
| 1 4 |
Matriz B:
| 0 1 |
| 5 2 |
Matriz A:
| 4 2 |
| 3 1 |
Matriz B:
| 1 0 |
| 2 5 |
¡No te preocupes si no lo logras a la primera! La práctica es clave, y con el tiempo, te volverás un experto en multiplicar matrices.
Aplicaciones de la Multiplicación de Matrices
¿Te has preguntado dónde se aplica la multiplicación de matrices en el mundo real? Aquí hay algunas áreas donde juega un papel crucial:
- Gráficos por Computadora: Las matrices se utilizan para transformar imágenes y modelos en 3D.
- Estadística: En análisis de datos, las matrices ayudan a manejar grandes conjuntos de datos.
- Redes Neuronales: En inteligencia artificial, las matrices son fundamentales para el aprendizaje automático.
Así que, la próxima vez que veas gráficos impresionantes en un videojuego o una aplicación de inteligencia artificial, recuerda que detrás de todo eso hay una buena cantidad de multiplicación de matrices.
¿Se pueden multiplicar matrices de diferentes tamaños?
No, para multiplicar matrices, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda. Así que, si tienes una matriz 2×3, solo puedes multiplicarla por una matriz de 3xN.
¿La multiplicación de matrices es conmutativa?
No, la multiplicación de matrices no es conmutativa. A veces A * B es diferente de B * A. ¡Así que cuidado con el orden!
¿Cómo se multiplica una matriz por un escalar?
Multiplicar una matriz por un escalar es mucho más sencillo. Solo multiplicas cada elemento de la matriz por el escalar. Por ejemplo, si tienes 3 * Matriz A, simplemente multiplica cada elemento de A por 3.
¿Dónde puedo encontrar más ejercicios sobre multiplicación de matrices?
Hay muchos recursos en línea, desde sitios web educativos hasta aplicaciones que ofrecen ejercicios prácticos. ¡Solo busca «ejercicios de multiplicación de matrices» y encontrarás un montón de opciones!
Así que ahí lo tienes, una guía completa sobre cómo multiplicar matrices 2×2. Espero que te haya sido útil y que ahora te sientas más seguro al abordar este tema. ¡Hasta la próxima!