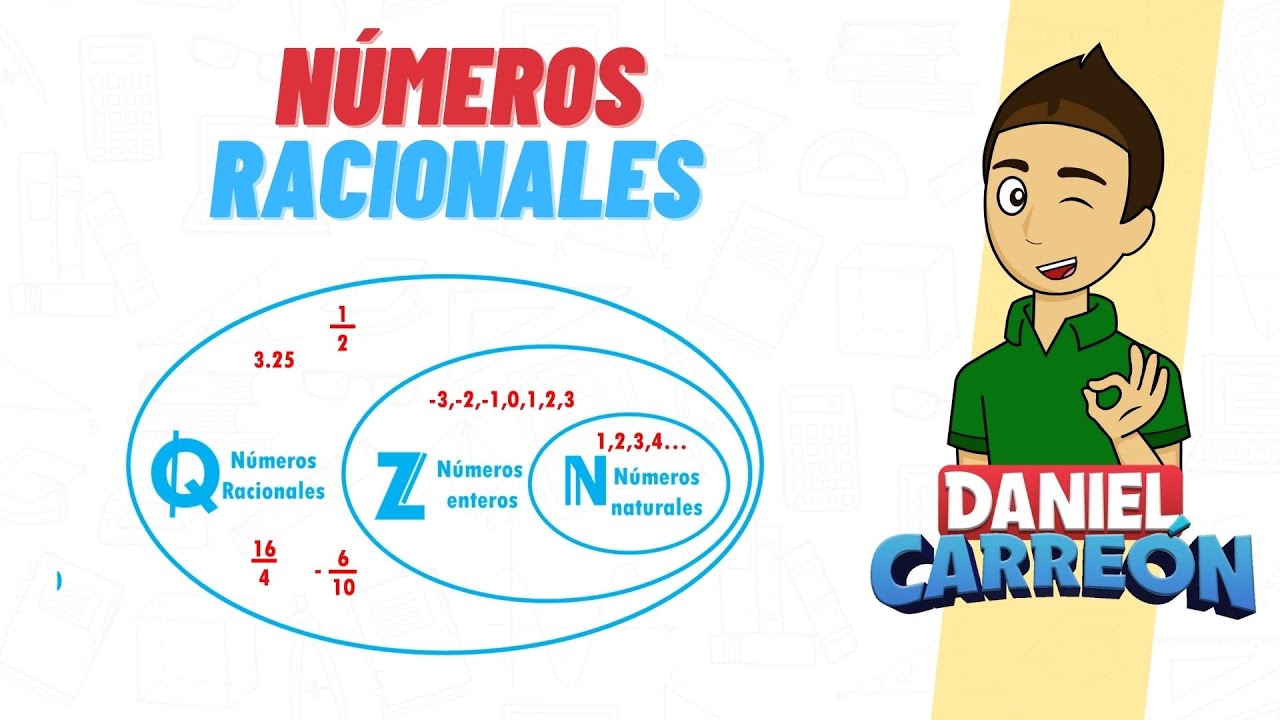
¡Hola! Hoy vamos a sumergirnos en el fascinante mundo de los números racionales. ¿Te has preguntado alguna vez qué son exactamente? Bueno, para empezar, un número racional es cualquier número que se puede expresar como el cociente de dos enteros, donde el denominador no puede ser cero. Es como esa pizza que compartes con tus amigos: si tienes 8 porciones y decides compartirlas, cada amigo recibe una parte de esa deliciosa pizza. En términos matemáticos, eso se traduce a algo como 3/8. ¡Y eso es un número racional!
¿Por qué son importantes los números racionales? Imagínate que estás en un supermercado y ves un precio de $3.75. ¡Eso es un número racional en acción! Comprender los números racionales es esencial no solo en matemáticas, sino en la vida diaria. Desde calcular descuentos hasta dividir cuentas, los números racionales son tus mejores amigos. Así que, ¿estás listo para mejorar tu comprensión de ellos? ¡Vamos a ello!
¿Cómo Identificar Números Racionales?
Primero, hablemos sobre cómo identificar un número racional. No te preocupes, no necesitas ser un genio matemático para hacerlo. Si puedes escribir un número en forma de fracción, ¡felicitaciones! Estás tratando con un número racional. Por ejemplo, 0.5 es igual a 1/2, y 3.75 se puede expresar como 15/4. Incluso los números negativos pueden ser racionales, como -2/3. ¿Ves cómo se puede encontrar un número racional en casi cualquier lugar?
Ejemplos de Números Racionales
Ahora, vamos a poner esto en práctica. Aquí tienes algunos ejemplos de números que son racionales:
- 1/2
- -4/5
- 0.333… (que es 1/3)
- 7 (que es 7/1)
- -2.25 (que es -9/4)
¿Te das cuenta de que incluso los números decimales pueden ser racionales? Lo importante es que puedas expresarlos como fracciones. ¡Así de simple!
Operaciones con Números Racionales
Ahora que ya sabemos qué son y cómo identificarlos, es hora de hablar sobre cómo operar con ellos. Las operaciones básicas son la suma, resta, multiplicación y división. ¡No te asustes! Vamos a desglosar cada una de ellas para que te resulte más fácil.
Suma de Números Racionales
La suma de números racionales puede ser sencilla o un poco más complicada, dependiendo de si los denominadores son iguales o diferentes. Si son iguales, simplemente sumas los numeradores. Por ejemplo:
1/4 + 2/4 = (1 + 2)/4 = 3/4
Pero si los denominadores son diferentes, tendrás que encontrar un común denominador. Digamos que quieres sumar 1/3 y 1/6. Primero, debes encontrar el mínimo común múltiplo (MCM) de 3 y 6, que es 6. Luego, convierte 1/3 a una fracción con denominador 6:
1/3 = 2/6
Ahora puedes sumar:
2/6 + 1/6 = 3/6 = 1/2
Resta de Números Racionales
La resta funciona de manera muy similar a la suma. Utiliza el mismo principio de encontrar un común denominador si es necesario. Por ejemplo:
5/6 – 1/3. Primero, cambia 1/3 a 2/6, y luego resta:
5/6 – 2/6 = 3/6 = 1/2
Multiplicación de Números Racionales
Multiplicar números racionales es más sencillo. Simplemente multiplicas los numeradores entre sí y los denominadores entre sí. Por ejemplo:
(2/3) * (3/4) = (2 * 3) / (3 * 4) = 6/12 = 1/2
División de Números Racionales
La división de números racionales se puede ver como multiplicar por el recíproco. Por ejemplo:
(2/3) ÷ (4/5) es lo mismo que (2/3) * (5/4). Entonces:
(2 * 5) / (3 * 4) = 10/12 = 5/6
Ejercicios Prácticos
¡Ahora que ya conoces las operaciones, es hora de ponerlo en práctica! Aquí tienes algunos ejercicios para que puedas probar tus habilidades:
Ejercicio 1: Suma
Suma 1/2 + 1/4. ¿Cuál es el resultado?
Ejercicio 2: Resta
Resta 3/5 – 1/10. ¿Qué obtienes?
Ejercicio 3: Multiplicación
Multiplica 2/7 * 3/5. ¿Cuál es la respuesta?
Ejercicio 4: División
Divide 3/8 ÷ 1/2. ¿Qué resultado obtienes?
Soluciones a los Ejercicios
Ahora, vamos a ver las respuestas a los ejercicios que acabas de hacer:
Respuesta 1
1/2 + 1/4 = 2/4 + 1/4 = 3/4
Respuesta 2
3/5 – 1/10 = 6/10 – 1/10 = 5/10 = 1/2
Respuesta 3
2/7 * 3/5 = 6/35
Respuesta 4
3/8 ÷ 1/2 = 3/8 * 2/1 = 6/8 = 3/4
Importancia de los Números Racionales en la Vida Cotidiana
Quizás te estés preguntando: «¿Por qué debería preocuparme por los números racionales en mi vida diaria?» Bueno, imagina que estás cocinando. Las recetas a menudo requieren fracciones para medir ingredientes. Por ejemplo, si una receta pide 2/3 de taza de azúcar, ¿cómo vas a saber cuánto es eso si no entiendes los números racionales?
Además, en el mundo financiero, la comprensión de los números racionales es clave. Desde calcular el interés en un préstamo hasta dividir cuentas en un restaurante, los números racionales están en todas partes. Así que, no solo es importante para tus clases de matemáticas; ¡es esencial para la vida!
¿Los números enteros son también números racionales?
¡Sí! Todos los números enteros son números racionales porque pueden expresarse como fracciones con un denominador de 1. Por ejemplo, 5 se puede escribir como 5/1.
¿Qué pasa con los números decimales? ¿Todos son racionales?
No todos los números decimales son racionales. Los decimales que terminan o que tienen un patrón repetitivo son racionales (como 0.75 o 0.333…), mientras que los decimales que no terminan y no repiten, como π, no son racionales.
¿Cómo puedo practicar más sobre números racionales?
Hay muchos recursos en línea, desde juegos hasta ejercicios de práctica. También puedes crear tus propios problemas o pedir ayuda a un amigo. ¡La práctica es clave!
¿Los números racionales se utilizan en ciencias?
Absolutamente. En química, física y biología, los números racionales son fundamentales para medir cantidades, calcular proporciones y realizar experimentos.
Así que ahí lo tienes, una guía completa sobre los números racionales. Ahora, la próxima vez que veas una fracción, ¡sabrás exactamente qué es y cómo usarla! ¿Listo para salir y aplicar tus nuevos conocimientos? ¡Vamos a hacerlo!