¿Alguna vez te has preguntado cómo podemos visualizar datos de una manera que sea fácil de entender? ¡Aquí es donde entra el polígono de frecuencias relativas! Este término puede sonar un poco técnico, pero en realidad, es una herramienta bastante útil para aquellos que trabajan con datos estadísticos. A lo largo de este artículo, desglosaremos qué es un polígono de frecuencias relativas, cómo se construye y, lo más importante, cómo se puede aplicar en diversas situaciones. Prepárate para sumergirte en el fascinante mundo de la estadística de una manera sencilla y amigable.
Los polígonos de frecuencias relativas son gráficos que representan la distribución de un conjunto de datos, y lo hacen de una forma que es fácil de visualizar. En lugar de presentar los datos en tablas complicadas, este tipo de gráfico conecta puntos que representan las frecuencias relativas de diferentes categorías o intervalos. ¿Te suena complicado? No te preocupes, porque a medida que avancemos, verás que es más sencillo de lo que parece. Así que, sin más preámbulos, vamos a desglosar cada aspecto de este tema.
¿Qué es un Polígono de Frecuencias Relativas?
Para comenzar, hablemos de la definición básica. Un polígono de frecuencias relativas es un gráfico que muestra la frecuencia relativa de diferentes intervalos de datos. La frecuencia relativa es simplemente la proporción de veces que un valor o un grupo de valores aparece en un conjunto de datos, en comparación con el total. Por ejemplo, si tienes un conjunto de datos con 100 observaciones y 25 de ellas caen en un intervalo específico, la frecuencia relativa de ese intervalo sería 0.25 o 25%.
Ahora, ¿por qué querríamos utilizar un polígono de frecuencias relativas en lugar de otros tipos de gráficos? La respuesta es sencilla: la claridad. Este tipo de gráfico te permite ver de un vistazo cómo se distribuyen los datos, y también te ayuda a identificar patrones y tendencias. Es como mirar un mapa: en lugar de tener que leer cada calle y cada edificio, puedes ver rápidamente cómo se organiza todo.
Cómo Construir un Polígono de Frecuencias Relativas
Construir un polígono de frecuencias relativas no es tan complicado como parece. Aquí te dejo un paso a paso para que puedas hacerlo tú mismo:
Paso 1: Recolectar los Datos
El primer paso es tener un conjunto de datos. Puede ser cualquier cosa: las calificaciones de los estudiantes, las edades de los participantes en un evento, o incluso el número de veces que aparece una palabra en un texto. Lo importante es que los datos sean relevantes para la pregunta que estás tratando de responder.
Paso 2: Calcular las Frecuencias Relativas
Una vez que tengas tus datos, el siguiente paso es calcular las frecuencias relativas. Para hacer esto, simplemente cuentas cuántas veces aparece cada categoría o intervalo en tus datos y luego divides esa cantidad entre el total de observaciones. Recuerda, si tienes 100 datos y 25 caen en un intervalo específico, la frecuencia relativa es 0.25.
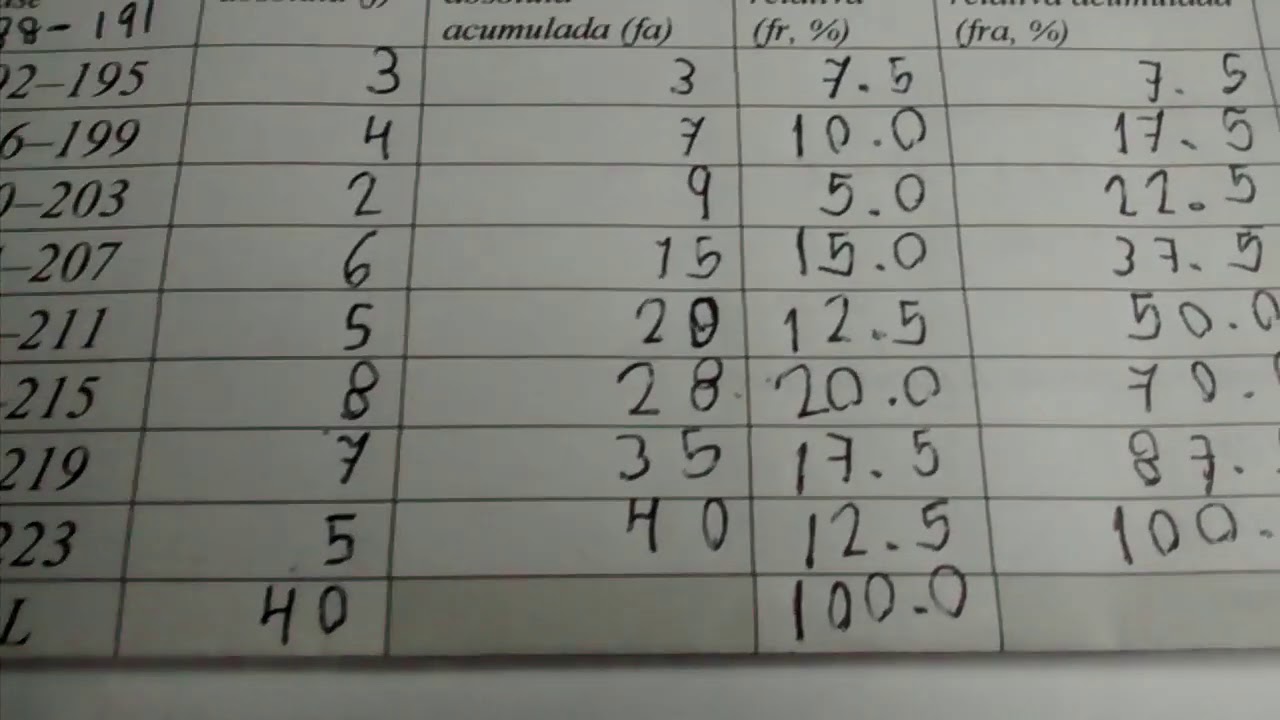
Paso 3: Crear una Tabla
Ahora que tienes tus frecuencias relativas, es útil organizarlas en una tabla. Esta tabla debe incluir las categorías o intervalos en una columna y las frecuencias relativas en otra. Esto te dará una visión clara de cómo se distribuyen tus datos.
Paso 4: Dibujar el Gráfico
Finalmente, es hora de dibujar el gráfico. Para hacerlo, coloca las frecuencias relativas en el eje Y y los intervalos en el eje X. Luego, marca un punto para cada intervalo en función de su frecuencia relativa y conecta los puntos con líneas. ¡Y voilà! Tienes tu polígono de frecuencias relativas.
Ejemplos Prácticos
Ahora que hemos cubierto cómo construir un polígono de frecuencias relativas, veamos algunos ejemplos prácticos para que todo quede más claro.
Ejemplo 1: Calificaciones de Estudiantes
Imagina que tienes las calificaciones de un grupo de estudiantes en un examen. Supongamos que las calificaciones están distribuidas en intervalos de 10 puntos (0-10, 11-20, etc.). Después de calcular las frecuencias relativas, podrías encontrar que el 30% de los estudiantes obtuvieron calificaciones entre 70 y 80. Al graficar esto, podrás ver rápidamente que la mayoría de los estudiantes se desempeñaron bien en ese intervalo.
Ejemplo 2: Edades de Participantes en un Evento
Supongamos que organizas un evento y registras las edades de los participantes. Si la mayoría de ellos tienen entre 20 y 30 años, el polígono de frecuencias relativas te mostrará claramente esa tendencia. Al observar el gráfico, podrías incluso decidir enfocar tu marketing en un grupo demográfico específico basado en esta información.
Aplicaciones del Polígono de Frecuencias Relativas
Los polígonos de frecuencias relativas no son solo gráficos bonitos; tienen aplicaciones en el mundo real que pueden ser muy útiles. Veamos algunas de ellas.
Análisis de Datos
En el ámbito de la investigación, los polígonos de frecuencias relativas son herramientas valiosas para analizar datos. Los investigadores pueden identificar patrones y tendencias que de otra manera podrían pasar desapercibidos en tablas de datos. Esto es especialmente útil en campos como la sociología, la psicología y el marketing.
Educación
En el contexto educativo, los maestros pueden utilizar polígonos de frecuencias relativas para evaluar el rendimiento de sus estudiantes. Al visualizar las calificaciones, pueden identificar áreas donde los estudiantes están luchando y ajustar su enseñanza en consecuencia.
Negocios
Las empresas pueden utilizar polígonos de frecuencias relativas para entender mejor a sus clientes. Por ejemplo, si una tienda de ropa observa que la mayoría de sus ventas se realizan en un rango de precios específico, puede ajustar su inventario para centrarse en esos productos.
Limitaciones del Polígono de Frecuencias Relativas
A pesar de sus ventajas, los polígonos de frecuencias relativas también tienen algunas limitaciones. Aquí hay un par de cosas a tener en cuenta:
Datos Discretos
Los polígonos de frecuencias relativas funcionan mejor con datos continuos. Si tienes datos discretos (como el número de hijos en una familia), es posible que un gráfico de barras sea más adecuado.
Interpretación Errónea
Si no se construyen correctamente, los polígonos de frecuencias relativas pueden llevar a interpretaciones erróneas. Por ejemplo, si no se incluyen todos los intervalos relevantes, podrías obtener una imagen distorsionada de los datos.
En resumen, el polígono de frecuencias relativas es una herramienta poderosa para visualizar y analizar datos. Nos permite ver de manera clara y concisa cómo se distribuyen nuestros datos, y puede aplicarse en una variedad de campos, desde la educación hasta los negocios. Así que la próxima vez que te enfrentes a un conjunto de datos, considera utilizar un polígono de frecuencias relativas para ayudarte a comprenderlo mejor.
¿Cuál es la diferencia entre un polígono de frecuencias relativas y un histograma?
La principal diferencia radica en la forma en que se representan los datos. Mientras que un histograma utiliza barras para mostrar la frecuencia de los intervalos, el polígono de frecuencias relativas conecta puntos que representan esas frecuencias.
¿Puedo usar un polígono de frecuencias relativas con datos cualitativos?
No es recomendable. Los polígonos de frecuencias relativas son más efectivos con datos cuantitativos, ya que estos permiten calcular frecuencias y frecuencias relativas de manera precisa.
¿Es necesario tener un software especializado para crear un polígono de frecuencias relativas?
No necesariamente. Puedes crear un polígono de frecuencias relativas a mano utilizando papel milimetrado, aunque también hay software y herramientas en línea que facilitan el proceso.
¿Qué otros gráficos son útiles para visualizar datos?
Además del polígono de frecuencias relativas, otros gráficos útiles incluyen gráficos de barras, gráficos de líneas y diagramas de dispersión, cada uno con sus propias ventajas dependiendo del tipo de datos que estés analizando.
¿Cómo puedo asegurarme de que mis datos sean precisos antes de crear un polígono de frecuencias relativas?
Es fundamental realizar una limpieza de datos, que incluye verificar que no haya errores tipográficos, duplicados y que todas las categorías estén correctamente representadas. Esto garantizará que tu polígono refleje la realidad de tus datos.