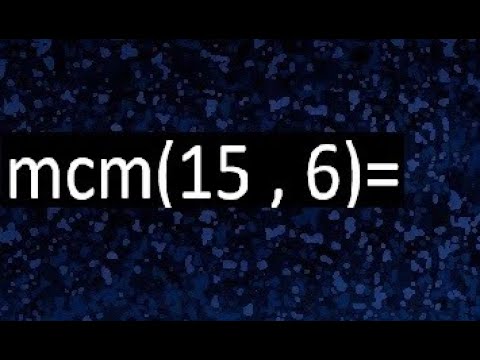Entendiendo el MCM y su Importancia
¿Alguna vez te has preguntado qué es el MCM y por qué es tan crucial en matemáticas? El MCM, o Mínimo Común Múltiplo, es un concepto que se encuentra en el corazón de muchas áreas de la matemática, desde la resolución de fracciones hasta la programación de eventos. Imagina que estás organizando una fiesta y necesitas coordinar la llegada de tus amigos que vienen en diferentes horarios. Aquí es donde el MCM se convierte en tu mejor amigo, ayudándote a encontrar el momento perfecto en que todos estarán disponibles.
Así que, cuando hablamos del MCM de dos números, en este caso, 15 y 6, estamos buscando el número más pequeño que es múltiplo de ambos. Pero antes de sumergirnos en los cálculos, es útil entender cómo llegamos allí y por qué este concepto es tan fascinante. ¡Vamos a desglosarlo!
¿Qué es el Mínimo Común Múltiplo?
El Mínimo Común Múltiplo es, en términos sencillos, el menor número que es un múltiplo de dos o más números. Por ejemplo, los múltiplos de 15 son 15, 30, 45, 60, y así sucesivamente. Por otro lado, los múltiplos de 6 son 6, 12, 18, 24, 30, etc. Si observas estos conjuntos de múltiplos, te darás cuenta de que el primer número que aparece en ambos es 30. ¡Y ahí lo tienes! El MCM de 15 y 6 es 30.
Pero, ¿por qué es importante conocer el MCM? En la vida cotidiana, el MCM se utiliza en situaciones como la planificación de eventos, la creación de horarios y la resolución de problemas de fracciones. Por ejemplo, si quieres sumar dos fracciones con diferentes denominadores, necesitas encontrar el MCM para poder hacerlo. Así que, en esencia, el MCM es una herramienta poderosa que nos ayuda a simplificar problemas complejos.
Cómo Calcular el MCM
Existen varios métodos para calcular el MCM, y cada uno tiene su propia utilidad. Vamos a explorar algunos de los más comunes.
Método de Listado de Múltiplos
Este es el método más simple y, a menudo, el más intuitivo. Todo lo que necesitas hacer es listar los múltiplos de ambos números hasta que encuentres el primero que se repita. Para nuestro caso:
– Múltiplos de 15: 15, 30, 45, 60…
– Múltiplos de 6: 6, 12, 18, 24, 30…
Como ya mencionamos, el primer múltiplo que aparece en ambas listas es 30. Por lo tanto, el MCM de 15 y 6 es 30.
Método de Factorización Prima
Si buscas un enfoque más matemático, puedes usar la factorización prima. Este método consiste en descomponer ambos números en sus factores primos y luego multiplicar los factores comunes y no comunes.
– 15 se descompone en 3 y 5.
– 6 se descompone en 2 y 3.
Ahora, tomamos todos los factores primos, usando cada uno la mayor cantidad de veces que aparece en cualquiera de las descomposiciones:
– Factores primos: 2, 3, 5
– Usamos: 2^1, 3^1, 5^1
Multiplicamos: 2^1 * 3^1 * 5^1 = 2 * 3 * 5 = 30.
Así que, nuevamente, llegamos a que el MCM de 15 y 6 es 30.
Aplicaciones Prácticas del MCM
Ahora que ya sabemos cómo calcular el MCM, es interesante pensar en algunas aplicaciones prácticas. ¿Te imaginas cuántas veces te puedes encontrar con este concepto en tu día a día?
Planificación de Eventos
Si estás organizando un evento, como una fiesta o una reunión, es posible que necesites coordinar a diferentes grupos que tienen horarios distintos. Supón que un grupo de amigos llega cada 15 minutos y otro cada 6 minutos. El MCM te dirá cuándo todos estarán presentes al mismo tiempo, lo que puede ser útil para actividades en grupo.
Resolución de Problemas de Fracciones
Si alguna vez has tenido que sumar o restar fracciones, sabes lo complicado que puede ser trabajar con diferentes denominadores. Aquí es donde el MCM entra en juego. Encuentras el MCM de los denominadores y lo usas para convertir las fracciones a un denominador común. Esto simplifica el proceso y te permite realizar operaciones más fácilmente.
Programación de Rutas
Imagina que eres un conductor de autobús y tienes dos rutas diferentes que se repiten en intervalos de 15 y 6 minutos. Usar el MCM te permitirá saber cada cuánto tiempo las dos rutas se cruzarán, lo que es esencial para una planificación eficiente.
El MCM es más que un simple concepto matemático; es una herramienta que podemos aplicar en diversas situaciones cotidianas. Desde organizar eventos hasta resolver fracciones, entender cómo funciona el MCM puede facilitarte la vida de maneras que nunca imaginaste. Así que la próxima vez que te enfrentes a dos números y te preguntes cuál es su MCM, recuerda que tienes varias herramientas a tu disposición.
Si bien hemos cubierto cómo calcular el MCM de 15 y 6, las aplicaciones son infinitas. Así que, ¿por qué no poner en práctica este conocimiento? Tal vez haya una fracción que necesites simplificar o un evento que debas planificar. ¡La matemática está en todas partes!
¿El MCM siempre es mayor que ambos números?
No necesariamente. El MCM puede ser igual a uno de los números si uno es múltiplo del otro. Por ejemplo, el MCM de 6 y 12 es 12.
¿Puedo calcular el MCM de más de dos números?
¡Por supuesto! Puedes calcular el MCM de tres o más números siguiendo el mismo proceso, ya sea listando los múltiplos o usando la factorización prima.
¿El MCM y el MCD son lo mismo?
No, el MCM (Mínimo Común Múltiplo) y el MCD (Máximo Común Divisor) son conceptos diferentes. El MCD es el número más grande que puede dividir a ambos números sin dejar residuo, mientras que el MCM es el menor número que es múltiplo de ambos.
¿Cómo se relacionan el MCM y el MCD?
Hay una relación interesante entre el MCM y el MCD. Para dos números a y b, se cumple que: MCM(a, b) * MCD(a, b) = a * b. Esto significa que si conoces uno, puedes calcular el otro.
¿Se puede calcular el MCM de números negativos?
El MCM se define generalmente para números enteros positivos. Sin embargo, si trabajas con números negativos, puedes ignorar el signo y calcular el MCM como lo harías normalmente.
¡Y ahí lo tienes! Un recorrido completo sobre el MCM de 15 y 6. Espero que ahora tengas una comprensión más clara y te sientas listo para aplicar este conocimiento en tu vida diaria. ¡Feliz cálculo!