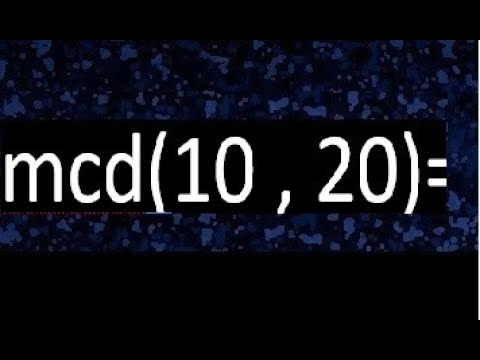¿Alguna vez te has encontrado en una situación donde necesitas encontrar el máximo común divisor (MCD) de dos números? No te preocupes, ¡estás en el lugar correcto! En este artículo, vamos a desglosar el proceso de calcular el MCD de 10 y 20, y lo haremos de una manera sencilla y comprensible. Antes de entrar en detalles, permíteme explicarte brevemente qué es el MCD y por qué es importante.
El MCD es el número más grande que puede dividir a dos o más números sin dejar un residuo. Imagina que tienes un grupo de amigos y quieres repartir dulces de manera equitativa. El MCD te dirá cuántos dulces puede recibir cada amigo sin que sobre ninguno. En nuestro caso, vamos a ver cómo 10 y 20 pueden ser divididos equitativamente. ¡Vamos a sumergirnos en este tema!
¿Qué es el Máximo Común Divisor?
Antes de calcular el MCD de 10 y 20, es útil entender el concepto en sí. El MCD es fundamental en matemáticas, especialmente en la teoría de números. Es una herramienta valiosa que se utiliza en diversas aplicaciones, desde simplificar fracciones hasta resolver problemas de álgebra.
Por ejemplo, si estás simplificando la fracción 10/20, el MCD te ayudará a reducirla a su forma más simple. En este caso, el MCD de 10 y 20 es 10, lo que significa que puedes dividir tanto el numerador como el denominador por 10 y obtener 1/2. Pero no nos adelantemos; primero, veamos cómo calcular el MCD paso a paso.
Métodos para Calcular el MCD
Existen varios métodos para calcular el MCD, pero hoy nos enfocaremos en dos de los más comunes: el método de factores primos y el método de divisiones sucesivas. Ambos son efectivos, así que elige el que más te guste.
Método de Factores Primos
Este método consiste en descomponer cada número en sus factores primos. Para el 10, los factores primos son 2 y 5, ya que 10 = 2 x 5. Por otro lado, el 20 se descompone en 2 x 2 x 5 (o 2² x 5). Ahora, ¿cómo encontramos el MCD?
1. Descomponemos los números:
– 10 = 2 x 5
– 20 = 2² x 5
2. Identificamos los factores comunes: Observamos que ambos números comparten el 2 y el 5.
3. Tomamos el menor exponente de cada factor: Para el 2, el menor exponente es 1 (de 2^1 en 10), y para el 5, es 1 (de 5^1 en ambos).
4. Multiplicamos los factores comunes: Así que, MCD(10, 20) = 2^1 x 5^1 = 2 x 5 = 10.
¡Y ahí lo tienes! El MCD de 10 y 20 es 10.
Método de Divisiones Sucesivas
Ahora, veamos el método de divisiones sucesivas, que es bastante directo. Este método implica dividir los números entre sí y continuar el proceso hasta que obtengamos un residuo de 0.
1. Dividimos el número mayor entre el menor: Comenzamos dividiendo 20 entre 10. Esto nos da un cociente de 2 y un residuo de 0.
2. Si el residuo es 0, el divisor (10 en este caso) es el MCD.
Así que, una vez más, llegamos a que el MCD de 10 y 20 es 10.
Ejemplos Prácticos
Para que el proceso sea más claro, consideremos algunos ejemplos prácticos que involucran otros números. Supongamos que quieres encontrar el MCD de 24 y 36. ¿Cómo lo harías?
1. Método de Factores Primos:
– 24 = 2³ x 3
– 36 = 2² x 3²
Los factores comunes son 2 y 3. Tomamos los menores exponentes: 2² y 3¹. Así que MCD(24, 36) = 2² x 3¹ = 4 x 3 = 12.
2. Método de Divisiones Sucesivas:
– Dividimos 36 entre 24, lo que nos da un cociente de 1 y un residuo de 12.
– Ahora, dividimos 24 entre 12, lo que nos da un cociente de 2 y un residuo de 0.
Por lo tanto, el MCD de 24 y 36 es 12.
Aplicaciones del MCD
Ahora que sabes cómo calcular el MCD, es importante entender cómo se utiliza en la vida real. Aquí hay algunas aplicaciones prácticas:
Simplificación de Fracciones
Como mencionamos antes, el MCD es crucial para simplificar fracciones. Si tienes la fracción 18/24, primero calculas el MCD, que es 6. Luego, divides ambos números por 6 para obtener 3/4.
Resolución de Problemas de Proporciones
En situaciones donde necesitas dividir recursos, como repartir pizzas entre amigos, el MCD te ayuda a asegurarte de que todos reciban una porción equitativa sin desperdiciar.
Algebra y Ecuaciones
El MCD también juega un papel en la resolución de ecuaciones algebraicas y sistemas de ecuaciones. Te permite simplificar términos y hacer que las ecuaciones sean más manejables.
Consejos para Recordar
Antes de terminar, aquí hay algunos consejos útiles para recordar al calcular el MCD:
1. Practica con diferentes números: Cuanto más practiques, más fácil te será encontrar el MCD.
2. Usa calculadoras en línea: Si alguna vez te sientes atascado, hay herramientas en línea que pueden hacer el trabajo por ti.
3. Recuerda los factores primos: Familiarízate con los factores primos de los números comunes, esto te ayudará a calcular el MCD más rápidamente.
¿Cuál es la diferencia entre el MCD y el Mínimo Común Múltiplo (MCM)?
El MCD es el mayor número que puede dividir dos o más números, mientras que el MCM es el menor número que es múltiplo de dos o más números.
¿Puedo calcular el MCD de más de dos números?
Sí, puedes calcular el MCD de más de dos números. Simplemente calcula el MCD de los dos primeros números y luego usa ese resultado para calcular el MCD con el siguiente número.
¿Existen algoritmos para calcular el MCD de forma más rápida?
Sí, el algoritmo de Euclides es un método eficiente para calcular el MCD y se basa en la resta y divisiones sucesivas.
¿Qué pasa si los números son negativos?
El MCD se define para números enteros, así que puedes ignorar el signo y calcular el MCD de los valores absolutos.
¿El MCD de dos números consecutivos siempre es 1?
Sí, dos números consecutivos no comparten factores primos, así que su MCD es 1.
Espero que esta guía te haya ayudado a entender cómo calcular el MCD de 10 y 20, así como la importancia de este concepto en matemáticas. ¡Ahora es tu turno de practicar y convertirte en un experto en MCD!