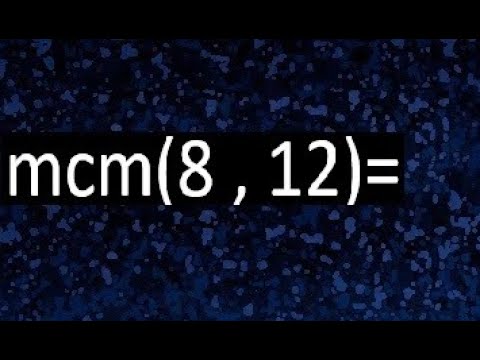Entendiendo el MCM: ¿Qué es y por qué es importante?
¡Hola! Hoy vamos a adentrarnos en el fascinante mundo de las matemáticas, específicamente en cómo calcular el Mínimo Común Múltiplo (MCM) de dos números: 8 y 12. Pero, ¿qué es exactamente el MCM? Imagina que tienes dos amigos que se reúnen cada cierto tiempo, uno cada 8 días y el otro cada 12 días. El MCM sería el día en que ambos coinciden en la misma reunión. Así que, en este artículo, te llevaré paso a paso por el proceso de cálculo del MCM de 8 y 12, y lo haremos de una manera sencilla y práctica. Vamos a desglosarlo, porque sé que a veces los números pueden parecer intimidantes. ¡Así que, sin más preámbulos, empecemos!
¿Qué es el Mínimo Común Múltiplo?
Antes de sumergirnos en los cálculos, es crucial entender qué significa Mínimo Común Múltiplo. El MCM de dos o más números es el múltiplo más pequeño que es común a todos ellos. Es decir, es el primer número que aparece en la lista de múltiplos de cada uno de los números. Para 8 y 12, queremos encontrar ese número mágico que ambos comparten. Suena un poco complicado, pero no te preocupes, ¡lo haremos juntos!
Pasos para Calcular el MCM de 8 y 12
Encuentra los múltiplos de cada número
Comencemos encontrando los múltiplos de 8 y 12. ¿Cómo se hace esto? Simplemente multiplicamos cada número por 1, 2, 3, y así sucesivamente. Aquí tienes los primeros múltiplos:
- Múltiplos de 8: 8, 16, 24, 32, 40, 48, …
- Múltiplos de 12: 12, 24, 36, 48, 60, …
Ahora, echemos un vistazo a estas listas. ¿Ves algún número que se repita? ¡Exacto! El primer múltiplo común que encontramos es 24. Así que, hasta ahora, parece que el MCM podría ser 24, pero sigamos confirmándolo con otros métodos.
Método de la descomposición en factores primos
Este método puede sonar un poco más técnico, pero en realidad es bastante simple. Lo que haremos es descomponer ambos números en sus factores primos. Esto nos dará una visión más clara de qué números están involucrados. Vamos a hacerlo:
- 8 se descompone en: 2 x 2 x 2 = 2³
- 12 se descompone en: 2 x 2 x 3 = 2² x 3¹
Ahora, para encontrar el MCM, tomamos cada factor primo y lo elevamos a la mayor potencia que aparece en cualquiera de las descomposiciones. En este caso, tenemos:
- Para el 2: la mayor potencia es 2³ (de 8)
- Para el 3: la mayor potencia es 3¹ (de 12)
Entonces, el MCM se calcula así: MCM = 2³ x 3¹ = 8 x 3 = 24. ¡Bingo! Nuevamente llegamos al mismo resultado.
Método de la lista de múltiplos
Si prefieres un enfoque más visual, siempre puedes simplemente listar los múltiplos de cada número hasta que encuentres el primero que se repite. Esto es especialmente útil si estás trabajando con números más pequeños o si simplemente prefieres ver las cosas de manera más gráfica. Como ya vimos, los múltiplos de 8 son 8, 16, 24, 32, … y los múltiplos de 12 son 12, 24, 36, … ¡Y aquí está 24 otra vez!
Ejemplo práctico: ¿Por qué es útil el MCM?
Ahora que hemos encontrado el MCM de 8 y 12, es posible que te preguntes por qué es tan importante. Imagina que eres un maestro y tienes dos grupos de estudiantes que necesitan hacer un proyecto. Un grupo tiene que presentar cada 8 días y el otro cada 12 días. Si deseas que ambos grupos presenten el mismo día, necesitarás coordinarse para que esto suceda. El MCM te dice exactamente cuándo deben hacerlo: ¡cada 24 días!
Otras formas de calcular el MCM
Si bien hemos cubierto varios métodos, hay otros enfoques que también puedes considerar. Algunos de ellos son:
Método de la regla de tres
Este es un método menos común, pero a veces puede ser útil. Básicamente, puedes usar la regla de tres para encontrar el MCM si tienes una relación directa entre los números. Sin embargo, es un poco más complicado y, en general, no se utiliza tanto como los métodos que ya discutimos.
Uso de calculadoras
Hoy en día, las calculadoras en línea pueden hacer el trabajo pesado por ti. Solo tienes que ingresar los números y te dirán el MCM en un instante. Pero, ¿dónde está la diversión en eso? Aprender a calcularlo tú mismo es una habilidad que te será útil en el futuro.
Resumiendo lo aprendido
En resumen, calcular el MCM de 8 y 12 puede hacerse de varias maneras: encontrando múltiplos, descomponiendo en factores primos o usando listas. Todos estos métodos nos llevan al mismo resultado: 24. Recuerda que el MCM es una herramienta valiosa en muchas situaciones cotidianas, especialmente cuando se trata de coordinar eventos o tareas. Así que la próxima vez que te enfrentes a un par de números, ¡no dudes en calcular su MCM!
¿El MCM siempre es mayor que los números originales?
No necesariamente. En algunos casos, como cuando los números son iguales, el MCM será el mismo número. Pero en general, el MCM tiende a ser mayor que los números originales.
¿Puedo calcular el MCM de más de dos números?
¡Claro! Puedes calcular el MCM de tres o más números utilizando los mismos métodos que hemos discutido. Simplemente asegúrate de considerar todos los factores primos involucrados.
¿Cuál es la diferencia entre MCM y MCD?
El Mínimo Común Múltiplo (MCM) es el múltiplo más pequeño que es común a dos o más números, mientras que el Máximo Común Divisor (MCD) es el número más grande que puede dividir a dos o más números sin dejar residuo. Son conceptos diferentes pero igualmente útiles.
¿Por qué es importante el MCM en la vida diaria?
El MCM es útil en situaciones donde necesitas sincronizar eventos, como en programación de tareas, planificación de proyectos o incluso en juegos de estrategia. Te ayuda a organizar mejor tus actividades y a trabajar de manera más eficiente.
¿Puedo usar el MCM para resolver problemas de fracciones?
Sí, el MCM es útil cuando sumas o restas fracciones con denominadores diferentes. Te ayuda a encontrar un denominador común, facilitando el proceso de suma o resta.
Así que ahí lo tienes, una guía completa sobre cómo calcular el MCM de 8 y 12. Espero que te haya sido útil y que ahora te sientas más seguro al tratar con números. ¡Hasta la próxima!