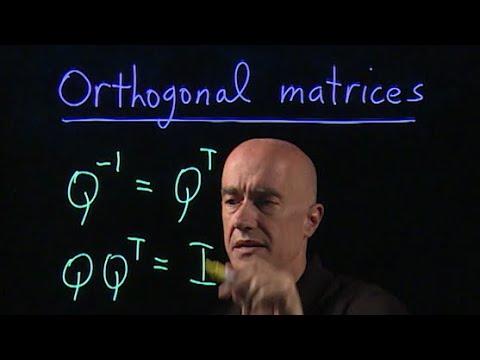Las matrices ortogonales son un concepto fascinante dentro del mundo del álgebra lineal. ¿Alguna vez te has preguntado cómo los matemáticos logran resolver sistemas de ecuaciones o transformar datos sin perder información? Las matrices ortogonales juegan un papel crucial en este proceso. Imagina que tienes un conjunto de datos en un espacio tridimensional, y quieres rotarlo sin cambiar su forma. Aquí es donde las matrices ortogonales entran en acción. Estas matrices, que se caracterizan por tener filas y columnas que son vectores ortogonales entre sí, ofrecen una serie de propiedades interesantes que las hacen ideales para diversas aplicaciones, desde gráficos por computadora hasta procesamiento de señales. Pero, ¿qué significa realmente que una matriz sea ortogonal? Vamos a desglosarlo.
Definición de Matriz Ortogonal
Una matriz cuadrada ( A ) se considera ortogonal si cumple con la condición ( A^T A = I ), donde ( A^T ) es la matriz transpuesta de ( A ) e ( I ) es la matriz identidad. Esto implica que las columnas (y filas) de la matriz son ortonormales, es decir, son perpendiculares entre sí y tienen una longitud de uno. Pero, ¿qué significa esto en términos más simples? Piensa en un sistema de coordenadas: si las líneas de un gráfico son ortogonales, se cruzan en ángulos rectos. De la misma manera, las columnas de una matriz ortogonal se «cruzan» de forma que no se solapan ni se distorsionan. Esta propiedad es fundamental en aplicaciones donde la preservación de la distancia y el ángulo es crucial.
Propiedades de las Matrices Ortogonales
Conservación de la Normativa
Una de las propiedades más interesantes de las matrices ortogonales es que conservan la longitud de los vectores. ¿Te imaginas lanzar una pelota en un campo de fútbol? La distancia que recorre la pelota no cambia, independientemente de cómo la gires, siempre y cuando no la toques. De forma similar, si aplicas una matriz ortogonal a un vector, la longitud de ese vector se mantendrá igual. Matemáticamente, esto se expresa como ( ||Av|| = ||v|| ), donde ( v ) es un vector y ( A ) es una matriz ortogonal.
Determinante Igual a Uno o Menos Uno
Otra propiedad importante es que el determinante de una matriz ortogonal es siempre igual a 1 o -1. Esto es relevante porque nos dice que, a pesar de que la matriz puede reflejar o rotar el espacio, no cambia el volumen. Es como cuando giras un cubo: su volumen permanece constante, solo cambia su orientación en el espacio.
Inversa Igual a la Transpuesta
Además, la inversa de una matriz ortogonal es igual a su transpuesta. Esto significa que si tienes una matriz ortogonal ( A ), puedes encontrar su inversa simplemente transponiéndola: ( A^{-1} = A^T ). Es como si tuvieras una receta: si quieres revertir un plato, simplemente sigues los pasos en orden inverso, y obtendrás el resultado original.
Ejemplos de Matrices Ortogonales
Ejemplo 1: La Matriz Identidad
Un ejemplo clásico de una matriz ortogonal es la matriz identidad ( I ). Esta matriz tiene 1s en la diagonal y 0s en todas las demás posiciones. Al multiplicar cualquier vector por la matriz identidad, el vector permanece inalterado, lo que demuestra que cumple con la propiedad de ortogonalidad. En este caso, ( I^T I = I ), confirmando que es ortogonal.
Ejemplo 2: Rotaciones en el Plano
Otro ejemplo son las matrices de rotación en el plano. Supón que deseas rotar un vector ( v ) en el plano ( xy ) un ángulo ( theta ). La matriz de rotación se expresa como:
[ R(theta) = begin{pmatrix}
cos(theta) & -sin(theta) \
sin(theta) & cos(theta)
end{pmatrix} ]
Esta matriz es ortogonal porque sus columnas son vectores unitarios y perpendiculares entre sí. Al aplicar esta matriz a un vector, se logra una rotación sin cambiar su longitud.
Aplicaciones de las Matrices Ortogonales
Procesamiento de Imágenes
Las matrices ortogonales son esenciales en el procesamiento de imágenes, especialmente en la compresión de datos. Por ejemplo, la Transformada Discreta de Coseno (DCT), utilizada en JPEG, emplea matrices ortogonales para transformar la imagen de un dominio espacial a un dominio de frecuencia. Esto permite reducir la cantidad de información necesaria para representar la imagen sin perder calidad notable.
Gráficos por Computadora
En gráficos por computadora, las matrices ortogonales se utilizan para realizar transformaciones de rotación y escalado. Si alguna vez has visto un modelo 3D girar en tu pantalla, es muy probable que se haya utilizado una matriz ortogonal para calcular su nueva orientación. La capacidad de rotar objetos sin distorsionarlos es crucial para crear gráficos realistas.
Análisis de Datos
En el análisis de datos, las matrices ortogonales se utilizan en técnicas como el Análisis de Componentes Principales (PCA). Este método ayuda a reducir la dimensionalidad de los datos al encontrar direcciones ortogonales que maximizan la varianza. Así, se pueden identificar patrones y tendencias en conjuntos de datos complejos.
Las matrices ortogonales son herramientas poderosas en matemáticas y sus aplicaciones son vastas y variadas. Desde la conservación de la longitud de los vectores hasta su uso en gráficos por computadora y procesamiento de imágenes, estas matrices son fundamentales en muchas disciplinas. Ahora que tienes una mejor comprensión de qué son y cómo funcionan, ¿te animas a explorar más sobre el álgebra lineal? Quizás te sorprenda todo lo que puedes hacer con estos conceptos matemáticos.
¿Por qué son importantes las matrices ortogonales en el álgebra lineal?
Las matrices ortogonales son importantes porque preservan la longitud y el ángulo de los vectores, lo que es fundamental en muchas aplicaciones, como la rotación y la transformación de datos.
¿Cómo puedo verificar si una matriz es ortogonal?
Para verificar si una matriz es ortogonal, debes calcular su transpuesta y multiplicarla por la matriz original. Si el resultado es la matriz identidad, entonces es ortogonal.
¿Las matrices ortogonales siempre tienen determinante 1 o -1?
Sí, el determinante de una matriz ortogonal siempre es 1 o -1, lo que significa que no alteran el volumen en el espacio al transformarlo.
¿Puedo crear una matriz ortogonal a partir de cualquier conjunto de vectores?
No necesariamente. Para que un conjunto de vectores forme una matriz ortogonal, deben ser linealmente independientes y deben ser ortogonales entre sí. Puedes usar el proceso de Gram-Schmidt para ortogonalizar un conjunto de vectores.
¿Qué papel juegan las matrices ortogonales en el aprendizaje automático?
En el aprendizaje automático, las matrices ortogonales se utilizan en algoritmos de reducción de dimensionalidad y en técnicas de regularización, donde ayudan a mejorar la estabilidad y la interpretabilidad de los modelos.
Espero que este artículo te haya proporcionado una comprensión clara y amena sobre las matrices ortogonales y su importancia en diversas aplicaciones. Si tienes más preguntas o te gustaría profundizar en algún tema específico, ¡no dudes en preguntar!