¿Te has preguntado alguna vez cómo se puede representar el mundo que nos rodea utilizando un simple gráfico? El plano cartesiano es una herramienta increíblemente poderosa que nos permite visualizar relaciones y patrones en los datos. Imagina que tienes un mapa de un tesoro y, en lugar de una X marcando el lugar, tienes un par de coordenadas que te indican exactamente dónde cavar. En este artículo, vamos a sumergirnos en el fascinante mundo del plano cartesiano, desglosando sus componentes y cómo puedes dominar su uso a través de ejercicios prácticos. ¡Prepárate para convertirte en un experto en la materia!
¿Qué es el Plano Cartesiano?
El plano cartesiano, también conocido como sistema de coordenadas cartesianas, es un sistema que permite ubicar puntos en un espacio bidimensional mediante un par de números, conocidos como coordenadas. Estas coordenadas se representan como (x, y), donde ‘x’ indica la posición horizontal y ‘y’ la vertical. Imagina que estás en un juego de video donde te mueves en un mapa; las coordenadas te indican tu ubicación exacta en ese mundo virtual. En este sentido, el plano cartesiano se convierte en tu mapa personal para entender mejor el espacio que te rodea.
Componentes del Plano Cartesiano
Para comprender el plano cartesiano, es crucial conocer sus componentes. La primera parte son los ejes: el eje horizontal se llama eje X y el eje vertical se llama eje Y. La intersección de estos dos ejes se llama origen, representado como (0, 0). Desde este punto, los números en el eje X aumentan hacia la derecha y disminuyen hacia la izquierda, mientras que en el eje Y, los números aumentan hacia arriba y disminuyen hacia abajo. ¿Te imaginas un juego de coordenadas donde el origen es el punto de partida y cada movimiento te lleva a un nuevo lugar? Esa es la esencia del plano cartesiano.
Cómo Leer las Coordenadas
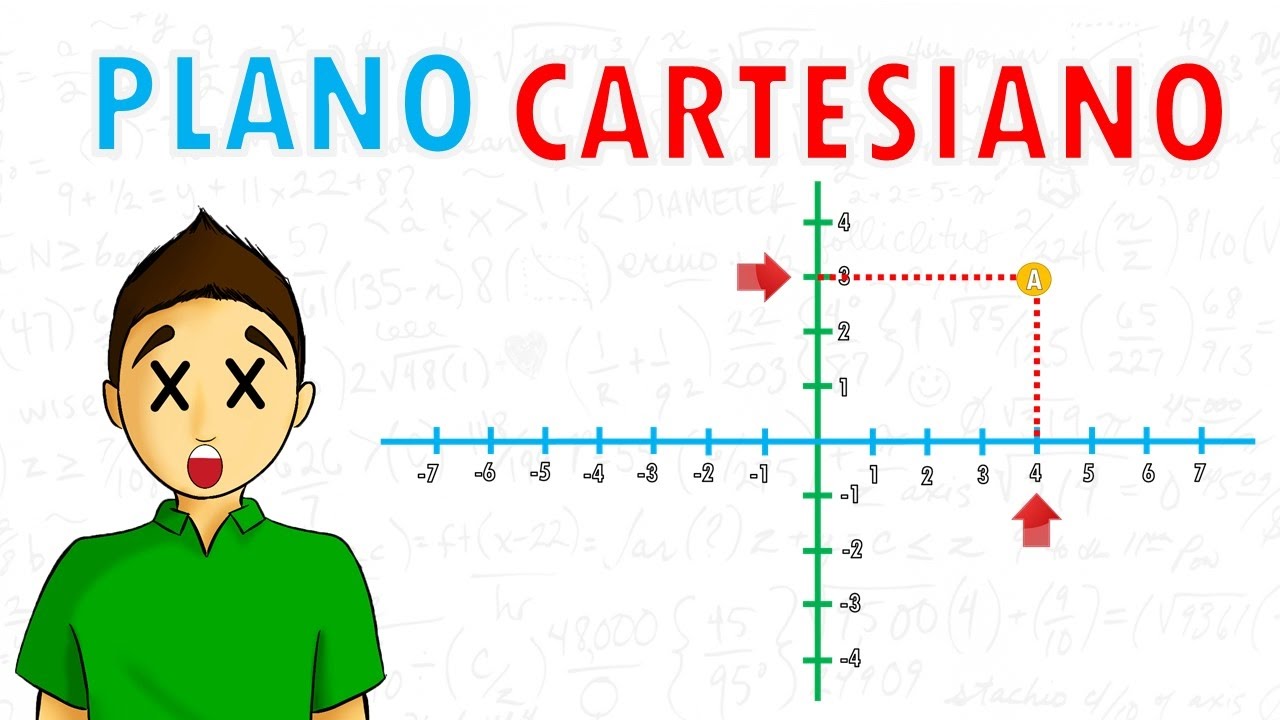
Leer coordenadas en el plano cartesiano es como leer un mapa. Cada par de números te lleva a un lugar específico. Por ejemplo, si tienes la coordenada (3, 2), te mueves 3 unidades a la derecha desde el origen y luego 2 unidades hacia arriba. Pero, ¿qué pasa si te encuentras con (−1, −4)? Ahí, te moverías 1 unidad a la izquierda y 4 unidades hacia abajo. Entender cómo se mueven estas coordenadas es clave para manejar el plano cartesiano con confianza.
Ejemplos Prácticos de Coordenadas
Para que esto sea más claro, consideremos algunos ejemplos prácticos. Supongamos que queremos ubicar puntos en un gráfico. Imagina que estás organizando una fiesta y necesitas colocar diferentes actividades en tu jardín. Puedes usar coordenadas para representar el lugar de cada actividad: una piñata en (2, 3), un área de comida en (4, 1) y un juego de sillas musicales en (1, 5). Visualizar estas ubicaciones en el plano cartesiano te permitirá planificar mejor tu evento. ¡Es como tener un plano de acción!
Ejercicios para Practicar el Uso del Plano Cartesiano
Ahora que tienes una comprensión básica, es hora de poner en práctica lo aprendido. Te propongo algunos ejercicios que te ayudarán a afianzar tus conocimientos. Recuerda, la práctica hace al maestro.
Ejercicio 1: Ubicación de Puntos
Ubica los siguientes puntos en un gráfico: (2, 5), (−3, 1), (0, −4), (4, 2). Una vez que los hayas marcado, trata de conectar los puntos en el orden que desees. ¿Qué figura se forma? Puede ser un triángulo, un cuadrado o algo completamente único. La creatividad es tu mejor aliada aquí.
Ejercicio 2: Identificación de Cuadrantes
El plano cartesiano se divide en cuatro cuadrantes. El cuadrante I está en la parte superior derecha, el II en la parte superior izquierda, el III en la parte inferior izquierda y el IV en la parte inferior derecha. Toma algunas coordenadas al azar y trata de identificar en qué cuadrante se encuentran. Por ejemplo, (−2, 3) está en el cuadrante II. ¿Puedes encontrar ejemplos en cada cuadrante?
Aplicaciones del Plano Cartesiano en la Vida Real
El plano cartesiano no es solo una herramienta matemática; tiene aplicaciones en diversos campos. Desde la ingeniería hasta la economía, esta herramienta es fundamental. Por ejemplo, en la ingeniería civil, se utilizan coordenadas para diseñar edificios y carreteras. En economía, se pueden graficar datos para analizar tendencias de mercado. Así que la próxima vez que veas un gráfico, recuerda que detrás de esa imagen hay una historia que se cuenta a través de coordenadas.
Gráficos y Funciones
Las funciones son una parte esencial del plano cartesiano. Una función es una relación entre dos variables que puede representarse gráficamente. Por ejemplo, la ecuación y = 2x + 1 es una función lineal. Puedes graficar esta función y ver cómo se comporta a medida que cambian los valores de ‘x’. ¡Es como ver una película en la que cada punto cuenta una parte de la historia! Así que, ¿qué tal si intentas graficar algunas funciones tú mismo? Puede ser muy divertido.
Consejos para Dominar el Uso del Plano Cartesiano
Si deseas convertirte en un maestro del plano cartesiano, aquí hay algunos consejos prácticos que te ayudarán en el camino:
Practica Regularmente
La práctica constante es la clave. Cuanto más trabajes con coordenadas, más fácil te resultará visualizarlas y entenderlas. Dedica unos minutos cada día a resolver problemas o graficar funciones. Con el tiempo, te sentirás como un experto.
Usa Herramientas Visuales
Las herramientas visuales pueden ser de gran ayuda. Usa gráficos en línea, aplicaciones educativas o incluso papel milimetrado para practicar. Ver cómo se representan los puntos y las funciones puede facilitar mucho la comprensión.
Forma Grupos de Estudio
Aprender en grupo puede ser muy efectivo. Comparte tus conocimientos con amigos o compañeros y resuelvan problemas juntos. A veces, una explicación diferente puede hacer que todo tenga sentido.
Dominar el ejercicio en el plano cartesiano es una habilidad que puede abrirte muchas puertas, no solo en el ámbito académico, sino también en la vida diaria. Desde la planificación de eventos hasta la comprensión de conceptos más complejos en matemáticas y ciencias, el plano cartesiano es una herramienta invaluable. Así que, ¡no dudes en seguir practicando y explorando! Recuerda, cada nuevo punto que descubras es un paso más en tu camino hacia la maestría en esta fascinante área.
- ¿Por qué es importante el plano cartesiano? El plano cartesiano es fundamental para visualizar y analizar datos en matemáticas y ciencias, facilitando la comprensión de relaciones y patrones.
- ¿Cómo puedo practicar más el uso del plano cartesiano? Puedes resolver ejercicios en línea, graficar funciones y trabajar con problemas de ubicación de puntos en el plano.
- ¿Qué aplicaciones tiene el plano cartesiano en la vida real? Se utiliza en ingeniería, economía, diseño gráfico, y muchas otras áreas donde la representación visual de datos es clave.
- ¿Qué son las funciones y cómo se relacionan con el plano cartesiano? Las funciones son relaciones entre variables que se pueden graficar en el plano cartesiano, mostrando cómo una variable depende de otra.
- ¿Cuáles son los cuadrantes del plano cartesiano? El plano se divide en cuatro cuadrantes: I (positivo, positivo), II (negativo, positivo), III (negativo, negativo) y IV (positivo, negativo).