¿Alguna vez te has preguntado cómo se comportan los objetos cuando se deslizan por una superficie inclinada? Los planos inclinados son una parte fascinante de la física que nos ayuda a entender cómo la gravedad afecta a los objetos en movimiento. Imagina que tienes una rampa y decides dejar rodar una bola de tenis. ¿Qué crees que pasará? La bola acelerará, y la inclinación de la rampa influirá en su velocidad. En este artículo, vamos a explorar los conceptos fundamentales de los planos inclinados, resolver algunos ejercicios y, lo más importante, hacer que todo esto sea fácil de entender. ¡Vamos a ello!
Conceptos Básicos del Plano Inclinado
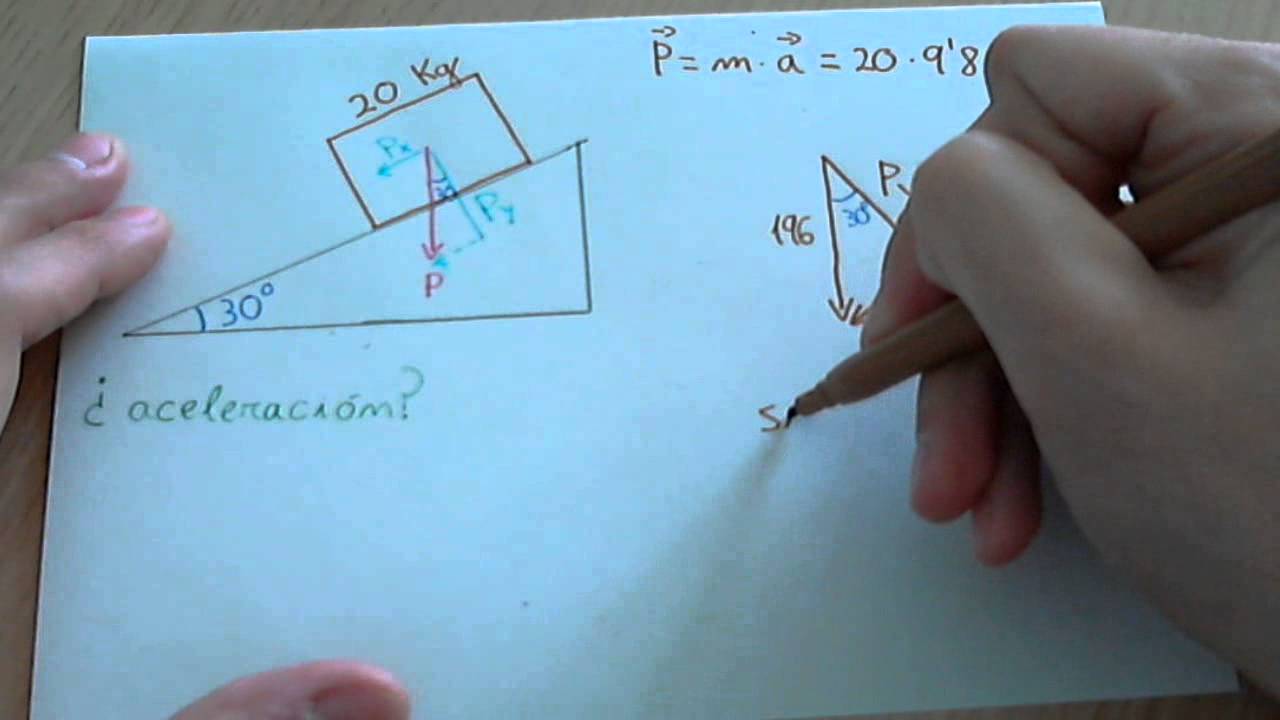
Antes de entrar en los ejercicios, es fundamental que entendamos algunos conceptos básicos. Un plano inclinado es una superficie que está inclinada respecto a la horizontal. La fuerza que actúa sobre un objeto en un plano inclinado se puede descomponer en dos componentes: la fuerza paralela al plano y la fuerza perpendicular al plano. La primera es la que provoca el movimiento del objeto, mientras que la segunda es la que actúa contra la normal del plano.
Descomposición de Fuerzas
Para visualizarlo mejor, imagina que estás empujando un carro de compras cuesta abajo en un supermercado. La fuerza de gravedad está tirando del carro hacia abajo, pero tú también estás empujando. Aquí, la gravedad se descompone en dos partes: una que empuja el carro hacia abajo a lo largo de la rampa (la componente paralela) y otra que empuja el carro hacia el lado del plano (la componente perpendicular). Esta descomposición es crucial para resolver problemas relacionados con el plano inclinado.
Ejercicio 1: Un Objeto en un Plano Inclinado Sin Fricción
Imaginemos que tenemos un bloque de 5 kg colocado sobre un plano inclinado que forma un ángulo de 30 grados con la horizontal. Queremos calcular la aceleración del bloque si no hay fricción.
Primero, descomponemos la fuerza de gravedad. La fuerza gravitacional (Fg) se calcula como:
math
Fg = m * g
donde ( m = 5 , kg ) y ( g = 9.81 , m/s^2 ).
Por lo tanto, ( Fg = 5 , kg * 9.81 , m/s^2 = 49.05 , N ).
Ahora, calculamos la componente de la fuerza que actúa a lo largo del plano:
math
F_{text{paralela}} = Fg * sin(theta)
donde ( theta = 30^circ ).
Entonces,
math
F_{text{paralela}} = 49.05 , N * sin(30^circ) = 49.05 , N * 0.5 = 24.525 , N.
Finalmente, para encontrar la aceleración (a), utilizamos la segunda ley de Newton:
math
F = m * a implies a = frac{F}{m}
Por lo tanto,
math
a = frac{24.525 , N}{5 , kg} = 4.905 , m/s^2.
Así que la aceleración del bloque es de aproximadamente ( 4.91 , m/s^2 ).
Ejercicio 2: Un Objeto en un Plano Inclinado con Fricción
Ahora, vamos a complicar un poco las cosas. Supongamos que el mismo bloque de 5 kg está en un plano inclinado de 30 grados, pero esta vez hay una fricción de 0.2 entre el bloque y el plano. Queremos encontrar la aceleración del bloque.
Primero, calculamos la fuerza de fricción (Ff). La fuerza de fricción se calcula como:
math
Ff = mu * F_{text{normal}}
Donde ( mu = 0.2 ). La fuerza normal se calcula como:
math
F_{text{normal}} = Fg * cos(theta) = 49.05 , N * cos(30^circ) = 49.05 , N * frac{sqrt{3}}{2} approx 42.43 , N.
Entonces,
math
Ff = 0.2 * 42.43 , N approx 8.486 , N.
Ahora, la fuerza neta (Fnet) que actúa sobre el bloque es:
math
F_{text{net}} = F_{text{paralela}} – Ff.
Ya calculamos ( F_{text{paralela}} ):
math
F_{text{net}} = 24.525 , N – 8.486 , N approx 16.039 , N.
Ahora, para encontrar la aceleración:
math
a = frac{F_{text{net}}}{m} = frac{16.039 , N}{5 , kg} approx 3.2078 , m/s^2.
Así que la aceleración del bloque con fricción es de aproximadamente ( 3.21 , m/s^2 ).
Ejercicio 3: Determinando la Fuerza de Fricción Necesaria
Ahora, supongamos que queremos que el bloque de 5 kg permanezca en reposo en un plano inclinado de 30 grados. ¿Qué fuerza de fricción sería necesaria para lograr esto?
Sabemos que la fuerza de gravedad que actúa a lo largo del plano es ( 24.525 , N ) (como calculamos anteriormente). Para que el bloque no se mueva, la fuerza de fricción debe igualar esta fuerza. Por lo tanto, la fuerza de fricción necesaria es de ( 24.525 , N ).
Ahora, podemos calcular el coeficiente de fricción necesario (( mu )) utilizando la fórmula:
math
Ff = mu * F_{text{normal}}.
Ya sabemos que ( F_{text{normal}} approx 42.43 , N ). Entonces:
math
24.525 , N = mu * 42.43 , N implies mu = frac{24.525 , N}{42.43 , N} approx 0.577.
Así que el coeficiente de fricción necesario para que el bloque permanezca en reposo es de aproximadamente ( 0.577 ).
Ejercicio 4: Determinando el Ángulo Crítico
Imaginemos que tenemos un plano inclinado y queremos saber en qué ángulo comenzará a deslizar un bloque de 5 kg si el coeficiente de fricción es de 0.3.
Para que el bloque esté en equilibrio, la fuerza de fricción debe igualar la componente paralela de la fuerza de gravedad. Por lo tanto:
math
mu * F_{text{normal}} = F_{text{paralela}}.
Reemplazando ( F_{text{normal}} ):
math
mu * (Fg * cos(theta)) = Fg * sin(theta).
Simplificando y reorganizando, tenemos:
math
mu * cos(theta) = sin(theta).
Dividiendo ambos lados por ( cos(theta) ):
math
mu = tan(theta).
Ahora, usando el coeficiente de fricción:
math
0.3 = tan(theta).
Para encontrar ( theta ):
math
theta = tan^{-1}(0.3) approx 16.7^circ.
Así que el ángulo crítico es de aproximadamente ( 16.7^circ ).
Los planos inclinados son un concepto básico pero fundamental en la física. A través de ejercicios prácticos, hemos aprendido a descomponer fuerzas, calcular aceleraciones y determinar fricciones. Estos conceptos son aplicables no solo en el aula, sino también en situaciones cotidianas.
Si alguna vez te encuentras en una rampa o simplemente observando cómo un objeto se desliza, recuerda que hay una serie de fuerzas en juego. La física está en todas partes, y comprender estos principios puede ayudarte a ver el mundo desde una nueva perspectiva.
¿Qué es un plano inclinado?
Un plano inclinado es una superficie que forma un ángulo con la horizontal, permitiendo que los objetos se deslicen hacia abajo debido a la gravedad.
¿Cómo afecta la fricción en un plano inclinado?
La fricción actúa en dirección opuesta al movimiento, reduciendo la aceleración de los objetos que se deslizan por el plano inclinado.
¿Cuál es la fórmula para calcular la aceleración en un plano inclinado?
La aceleración se puede calcular usando la segunda ley de Newton: ( a = frac{F_{text{net}}}{m} ), donde ( F_{text{net}} ) es la fuerza neta que actúa sobre el objeto.
¿Qué factores influyen en la fuerza normal en un plano inclinado?
La fuerza normal depende del peso del objeto y del ángulo del plano inclinado. A medida que aumenta el ángulo, la fuerza normal disminuye.
¿Por qué es importante entender los planos inclinados?
Comprender los planos inclinados es crucial para aplicar conceptos de física en situaciones cotidianas, como el diseño de rampas, la construcción de carreteras y en deportes como el esquí.