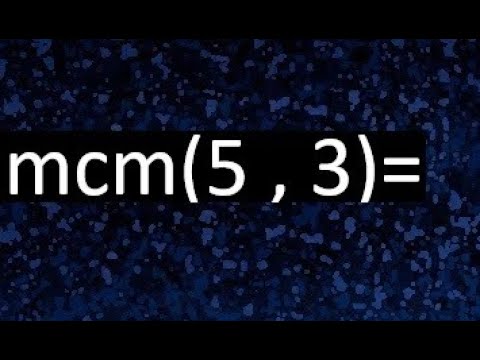¿Alguna vez te has preguntado cómo calcular el mínimo común múltiplo (MCM) de dos números? Es un concepto matemático que puede parecer complicado, pero en realidad es bastante sencillo una vez que lo entiendes. En este artículo, te guiaré paso a paso para calcular el MCM de 5 y 3, utilizando métodos prácticos que te ayudarán a hacerlo sin complicaciones. Así que, si estás listo, ¡comencemos!
¿Qué es el Mínimo Común Múltiplo?
El Mínimo Común Múltiplo es el menor número que es múltiplo de dos o más números. Imagina que estás organizando una fiesta y necesitas saber cuántas sillas comprar. Si tienes dos tipos de sillas, una que se apila de 5 en 5 y otra que se apila de 3 en 3, el MCM te dirá cuántas sillas necesitarás para que todas encajen perfectamente sin que sobren. Es una herramienta útil en la vida diaria y en problemas matemáticos.
Por qué es importante el MCM
Calcular el MCM puede ser crucial en diversas situaciones, desde la resolución de problemas de fracciones hasta la planificación de eventos. Por ejemplo, si estás organizando horarios de actividades y necesitas que se realicen en intervalos regulares, el MCM te ayudará a determinar cuándo coinciden. Es como encontrar el punto de encuentro perfecto entre dos caminos.
Métodos para Calcular el MCM
Existen varios métodos para calcular el MCM. Vamos a explorar dos de los más comunes: el método de descomposición en factores primos y el método de los múltiplos. Ambos son efectivos, pero pueden ser más o menos convenientes dependiendo de los números que estés tratando. ¡Vamos a ello!
Método 1: Descomposición en factores primos
Este método consiste en descomponer cada número en sus factores primos. Para el número 5, los factores primos son simplemente 5 (ya que es un número primo). Para el número 3, lo mismo ocurre; su único factor primo es 3. Ahora, tomamos todos los factores primos y los multiplicamos, eligiendo el mayor exponente de cada uno. En este caso, tenemos:
- Factores primos de 5: 51
- Factores primos de 3: 31
Ahora, multiplicamos estos factores:
MCM = 51 × 31 = 15
¡Y ahí lo tienes! El MCM de 5 y 3 es 15. Este método es muy efectivo, especialmente cuando los números son más grandes y tienen factores primos más complejos.
Método 2: Método de los múltiplos
El segundo método que vamos a ver es el de los múltiplos. Aquí, simplemente generamos los múltiplos de cada número hasta encontrar el más pequeño que sea común a ambos. Empecemos con el número 5:
- Múltiplos de 5: 5, 10, 15, 20, 25, …
Ahora, hagamos lo mismo con el número 3:
- Múltiplos de 3: 3, 6, 9, 12, 15, 18, …
Al observar ambos conjuntos de múltiplos, notamos que el primer múltiplo que tienen en común es 15. Por lo tanto, el MCM de 5 y 3 es 15. Este método es visual y puede ser más intuitivo para algunos, aunque puede volverse tedioso con números más grandes.
Comparando los Métodos
Ambos métodos son válidos, pero cada uno tiene sus ventajas y desventajas. La descomposición en factores primos es más rápida y eficiente para números grandes, mientras que el método de múltiplos puede ser más fácil de entender para principiantes. Si estás comenzando en el mundo de las matemáticas, puede que prefieras el segundo método hasta que te sientas más cómodo con el primero.
Ejemplos Adicionales
Para que te sientas más seguro, aquí hay algunos ejemplos adicionales que pueden ayudarte a practicar. Vamos a calcular el MCM de otros pares de números utilizando ambos métodos.
Ejemplo 1: MCM de 6 y 8
Primero, usando la descomposición en factores primos:
- Factores primos de 6: 21 × 31
- Factores primos de 8: 23
MCM = 23 × 31 = 24.
Ahora, usando el método de múltiplos:
- Múltiplos de 6: 6, 12, 18, 24, …
- Múltiplos de 8: 8, 16, 24, …
El primer múltiplo común es 24. Así que, el MCM de 6 y 8 es 24.
Ejemplo 2: MCM de 4 y 10
Usando la descomposición en factores primos:
- Factores primos de 4: 22
- Factores primos de 10: 21 × 51
MCM = 22 × 51 = 20.
Ahora, usando el método de múltiplos:
- Múltiplos de 4: 4, 8, 12, 16, 20, …
- Múltiplos de 10: 10, 20, …
El primer múltiplo común es 20. Así que, el MCM de 4 y 10 es 20.
Calcular el mínimo común múltiplo de dos números no tiene por qué ser un dolor de cabeza. Ya sea que uses la descomposición en factores primos o el método de múltiplos, lo importante es entender el concepto y practicar. Con el tiempo, te volverás un experto en esto y podrás aplicarlo a situaciones cotidianas.
¿El MCM siempre es mayor que los números originales?
No necesariamente. En algunos casos, el MCM puede ser igual a uno de los números si uno es un múltiplo del otro. Por ejemplo, el MCM de 4 y 8 es 8.
¿Se puede calcular el MCM de más de dos números?
¡Sí! Puedes calcular el MCM de tres o más números usando los mismos métodos. Simplemente calcula el MCM de dos números a la vez y luego usa ese resultado para calcular el MCM con el siguiente número.
¿Qué pasa si los números son negativos?
El MCM se define solo para números enteros no negativos. Si tienes números negativos, simplemente ignora el signo y calcula el MCM de los valores absolutos.
¿El MCM se puede usar en problemas de fracciones?
¡Absolutamente! El MCM es útil para encontrar un denominador común al sumar o restar fracciones. Al calcular el MCM de los denominadores, puedes convertir las fracciones para que tengan el mismo denominador.
Así que ahí lo tienes, una guía completa para calcular el Mínimo Común Múltiplo de 5 y 3, y más allá. Ahora que conoces estos métodos, ¿qué números te gustaría calcular a continuación?