¿Qué son las funciones lineales y por qué son importantes?
¡Hola, estudiantes de 2º de ESO! Hoy vamos a sumergirnos en un tema que, aunque puede parecer un poco intimidante al principio, es realmente fascinante: las funciones lineales. ¿Alguna vez te has preguntado cómo se relacionan las variables en el mundo real? Pues las funciones lineales son como esos mapas que nos ayudan a entender esas relaciones. Imagínate que quieres saber cuánto dinero ganarás si trabajas un número determinado de horas; eso es exactamente lo que hace una función lineal: te da una relación directa y sencilla entre dos variables.
Así que, ¡prepárate! Vamos a desglosar todo lo que necesitas saber sobre funciones lineales. Desde su definición hasta cómo graficarlas, pasando por algunos ejercicios prácticos que te ayudarán a entenderlas mejor. Y lo mejor de todo, lo haremos de manera que no te resulte aburrido. ¡Vamos a ello!
¿Qué es una función lineal?
Primero, definamos qué es una función lineal. En términos simples, una función lineal es una relación matemática que se puede expresar con una ecuación de la forma y = mx + b. Aquí, m representa la pendiente de la línea, mientras que b es el punto donde la línea cruza el eje y. Si piensas en una carretera recta, la pendiente sería la inclinación de esa carretera. ¿Es empinada o casi plana? El valor de m te lo dirá. Por otro lado, b es como el lugar donde comienzas tu viaje.
Componentes de la función lineal
Ahora que tenemos una idea básica de qué es una función lineal, profundicemos en sus componentes. La pendiente m se calcula como el cambio en y dividido por el cambio en x, es decir, m = (y2 – y1) / (x2 – x1). Esto nos dice cuán rápido cambia y cuando x cambia. Si la pendiente es positiva, la línea sube; si es negativa, baja. Por otro lado, el término b te dice el valor de y cuando x es cero. ¡Es como saber dónde empieza tu viaje antes de moverte!
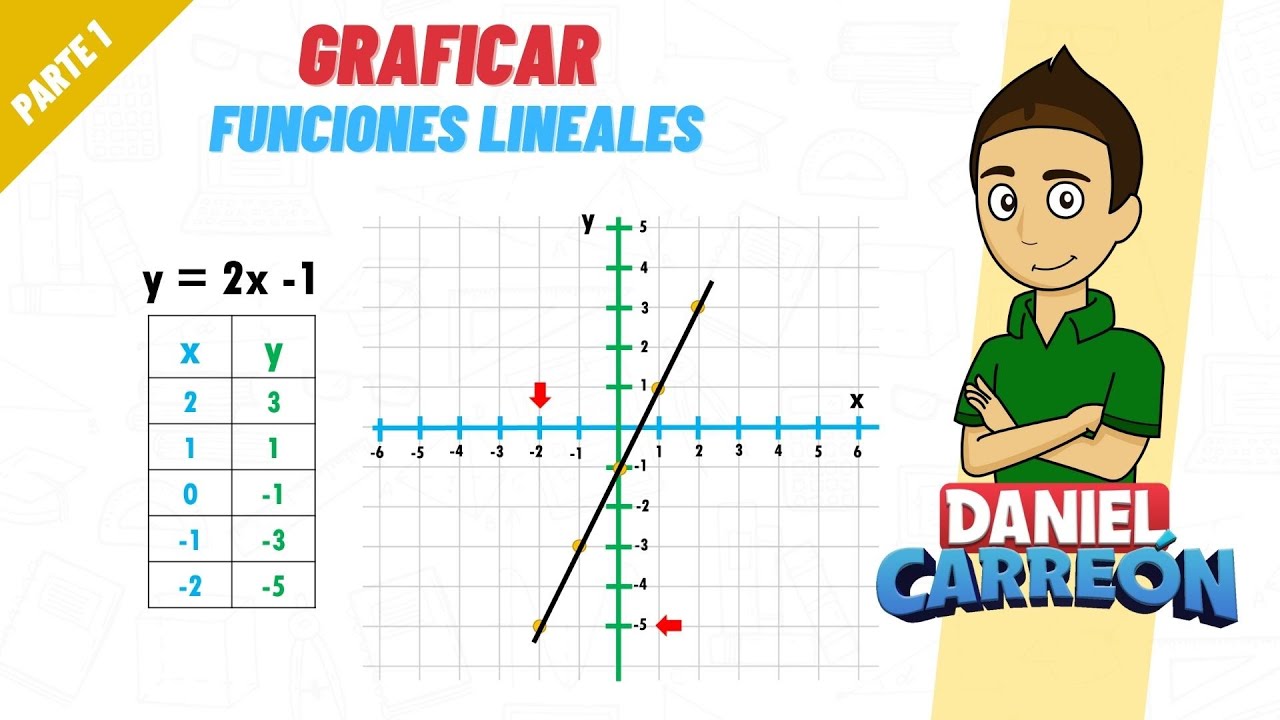
Graficando funciones lineales
Una de las habilidades más útiles que puedes aprender es cómo graficar funciones lineales. Imagina que tienes una hoja de papel y un lápiz. Primero, necesitarás un sistema de coordenadas, que es como un mapa. El eje x va de lado a lado, y el eje y va de arriba a abajo. Para graficar, sigue estos pasos:
- Identifica la pendiente y el intercepto: Si tienes la ecuación y = 2x + 3, sabes que la pendiente es 2 y el intercepto es 3.
- Marca el intercepto: Empieza por el punto (0, 3) en el eje y.
- Usa la pendiente: Desde el punto (0, 3), sube 2 unidades (porque la pendiente es 2) y muévete 1 unidad a la derecha. Eso te llevará al punto (1, 5).
- Conecta los puntos: Dibuja una línea recta a través de los puntos que has marcado.
¿Ves cómo se va formando la línea? Es como conectar los puntos en un dibujo. Cuantos más puntos traces, más precisa será tu línea. Y no te preocupes si al principio te resulta complicado; ¡la práctica hace al maestro!
Ejercicios prácticos
Ahora que ya sabes cómo funcionan las funciones lineales, es hora de poner a prueba tus habilidades. Aquí tienes algunos ejercicios prácticos:
Ejercicio 1: Encuentra la pendiente y el intercepto
Considera la ecuación y = -3x + 4. ¿Cuál es la pendiente y el intercepto? ¡Tómate un momento para pensarlo!
La pendiente es -3 (la línea desciende) y el intercepto es 4. ¡Buen trabajo!
Ejercicio 2: Graficar la función
Ahora, grafica la función anterior. Recuerda seguir los pasos que discutimos antes. Marca el intercepto en (0, 4) y luego desde ahí baja 3 unidades y muévete 1 a la derecha. ¿Puedes conectar esos puntos?
Ejercicio 3: Resolver un problema de la vida real
Imagina que tienes una tienda y vendes camisetas a 10 euros cada una. Tu costo inicial (el alquiler y otros gastos) es de 50 euros. Escribe la función que representa tus ingresos y en función del número de camisetas vendidas x. Luego, grafica esa función.
La ecuación sería y = 10x – 50. La pendiente es 10 y el intercepto es -50. Esto significa que antes de vender camisetas, estás en números rojos. ¡Es una buena manera de entender cómo funcionan los negocios!
Aplicaciones de las funciones lineales
Las funciones lineales no son solo un concepto matemático; tienen aplicaciones en el mundo real. Por ejemplo, se utilizan en economía para modelar costos y beneficios, en física para describir movimientos uniformes, e incluso en la programación para crear algoritmos que resuelven problemas complejos.
Funciones lineales en la economía
En economía, las funciones lineales son útiles para entender cómo los cambios en la producción afectan los costos. Si produces más, tus costos pueden aumentar de manera predecible. Esto es crucial para tomar decisiones informadas sobre producción y precios.
Funciones lineales en la física
En física, una función lineal puede describir la relación entre la distancia y el tiempo en un movimiento uniforme. Por ejemplo, si conduces a una velocidad constante, la distancia recorrida es una función lineal del tiempo. ¡Todo tiene su lógica!
¿Qué pasa si la pendiente es cero?
Si la pendiente es cero, significa que la línea es horizontal. Esto indica que no hay cambio en y a medida que x cambia. En otras palabras, ¡estás en un nivel constante!
¿Cómo sé si una función es lineal?
Una función es lineal si se puede expresar en la forma y = mx + b. Si al graficar los puntos obtienes una línea recta, ¡felicitaciones! Has encontrado una función lineal.
¿Las funciones lineales siempre cruzan el eje y?
Sí, todas las funciones lineales cruzan el eje y en el punto b. Este punto es esencial porque nos dice el valor de y cuando x es cero.
¿Pueden las funciones lineales tener pendiente negativa?
¡Absolutamente! Una pendiente negativa significa que la línea desciende a medida que te mueves hacia la derecha. Es como una colina; mientras más te alejas de la cima, más bajo estás.
Así que ahí lo tienes, una guía completa sobre funciones lineales. Espero que ahora tengas una mejor comprensión de este concepto y cómo aplicarlo en diferentes situaciones. ¡Practica y no dudes en hacer preguntas si algo no está claro! Las matemáticas pueden ser un viaje emocionante, y tú estás en el camino correcto.