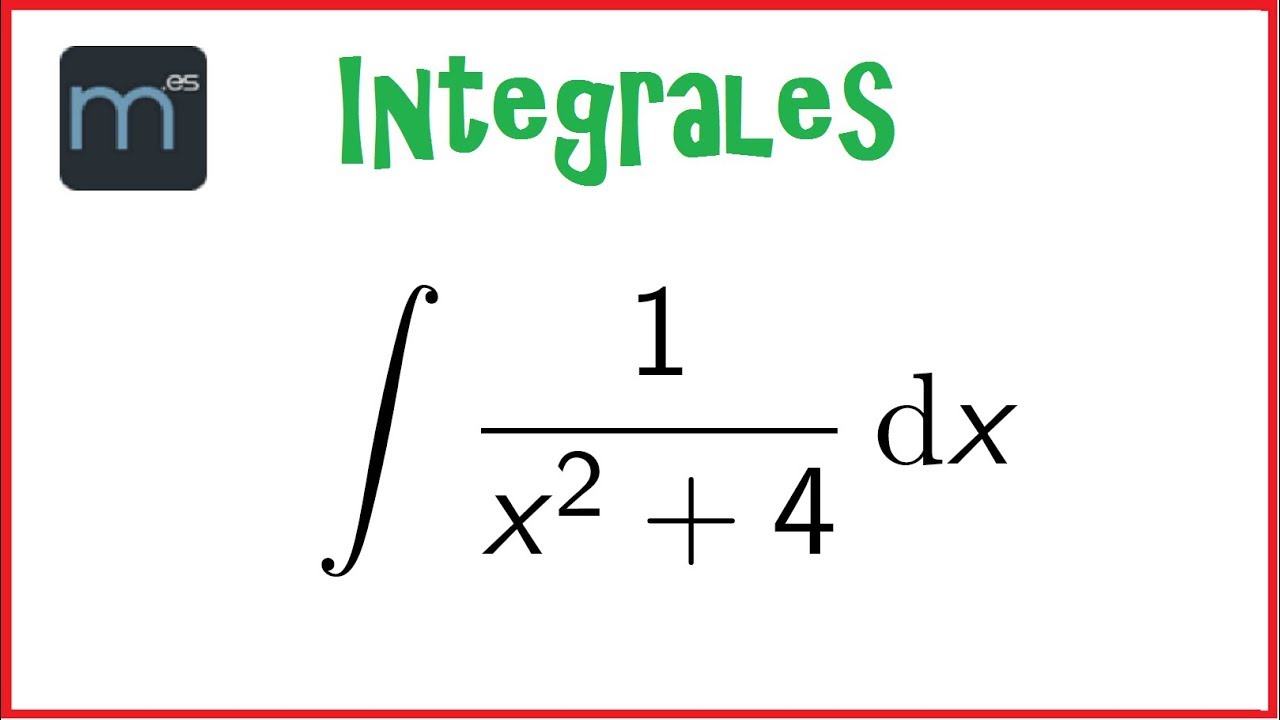Las integrales son un tema fascinante en el mundo del cálculo, y entre ellas, las integrales que involucran la función arcotangente tienen un lugar especial. ¿Alguna vez te has preguntado cómo se relacionan estas integrales con conceptos más amplios en matemáticas? En este artículo, exploraremos las integrales tipo arcotangente, desglosando sus características, propiedades y, por supuesto, ¡muchos ejemplos prácticos! Si estás listo para sumergirte en este emocionante viaje matemático, acompáñame. ¡Vamos a ello!
¿Qué es la Integral Tipo Arcotangente?
Primero, definamos qué es una integral tipo arcotangente. En términos simples, se refiere a aquellas integrales que pueden resolverse utilizando la función arcotangente, que es la inversa de la tangente. La forma más común de estas integrales aparece en expresiones que incluyen una fracción donde el numerador y el denominador son polinomios. Por lo general, tienen la forma:
∫ (1 / (a² + x²)) dx = (1/a) * arctan(x/a) + C
Donde «C» es la constante de integración. Esta fórmula es muy útil, y entenderla te permitirá resolver una variedad de problemas de manera más sencilla. Pero, ¿por qué es tan importante esta integral? La respuesta radica en su aplicación en diversos campos, desde la física hasta la ingeniería. ¡Imagina poder resolver problemas complejos con un simple conocimiento de esta integral!
La Importancia de la Integral Tipo Arcotangente
¿Alguna vez has considerado cómo se aplican las integrales en la vida real? La integral tipo arcotangente no es solo un concepto abstracto; tiene aplicaciones prácticas en el análisis de circuitos eléctricos, en la mecánica de fluidos y en la teoría de señales, entre otros. Por ejemplo, en la ingeniería, se utiliza para modelar fenómenos que involucran ángulos y pendientes. ¡Es como tener una herramienta mágica que te ayuda a desentrañar los secretos del mundo que te rodea!
¿Cuándo usar la Integral Tipo Arcotangente?
La integral tipo arcotangente es particularmente útil cuando te enfrentas a integrales que involucran expresiones cuadráticas. Si te encuentras con una integral que tiene la forma:
∫ (1 / (x² + a²)) dx
Entonces, ¡estás en el lugar correcto! Esta es la situación perfecta para aplicar la fórmula de la integral tipo arcotangente. Pero, espera, ¿cómo sabes si una integral es adecuada para esta técnica? Aquí hay algunos consejos: busca fracciones, especialmente aquellas donde el denominador tiene una forma cuadrática. Si ves eso, hay una buena posibilidad de que puedas usar la integral tipo arcotangente.
Ejemplo Práctico 1: Integral Simple
Ahora, pasemos a un ejemplo práctico. Supongamos que queremos resolver la siguiente integral:
∫ (1 / (x² + 4)) dx
En este caso, podemos identificar que «a²» es 4, lo que significa que «a» es 2. Aplicando la fórmula, tenemos:
∫ (1 / (x² + 4)) dx = (1/2) * arctan(x/2) + C
¡Y ahí lo tienes! La solución es simple y elegante. ¿Ves cómo la integral tipo arcotangente facilita la resolución de este tipo de problemas? Es como tener un mapa que te guía a través de un laberinto matemático.
Ejemplo Práctico 2: Integral con Cambio de Variable
Vamos a complicar un poco las cosas. Imagina que tenemos la integral:
∫ (3 / (x² + 9)) dx
Aquí, podemos notar que el denominador también es cuadrático. Sin embargo, primero debemos hacer un pequeño cambio de variable. Observa que podemos reescribir la integral como:
∫ (3 / (x² + 3²)) dx
Ahora, aplicamos la fórmula de la integral tipo arcotangente:
Esto nos da:
∫ (3 / (x² + 9)) dx = (3/3) * arctan(x/3) + C = arctan(x/3) + C
Una vez más, hemos logrado resolver la integral de manera efectiva. ¿No es impresionante cómo una simple técnica puede transformar un problema aparentemente complicado en algo manejable?
Ejemplo Práctico 3: Integral con Coeficientes
Veamos un ejemplo que incluye coeficientes. Supongamos que queremos resolver:
∫ (5x / (x² + 1)) dx
En este caso, notamos que el numerador es 5x. Esto sugiere que podemos aplicar un cambio de variable. Si hacemos u = x² + 1, entonces du = 2x dx, lo que nos permite reescribir la integral en términos de «u». Así, podemos expresar «x dx» como:
dx = du/(2x)
Ahora, sustituimos en la integral:
∫ (5 / u) (du/2) = (5/2) ∫ (1/u) du = (5/2) ln|u| + C
Finalmente, volvemos a sustituir «u» por «x² + 1»:
(5/2) ln|x² + 1| + C
Este ejemplo muestra cómo la integral tipo arcotangente puede ser parte de un proceso más amplio de resolución de integrales, utilizando cambios de variable y logaritmos. ¡La matemática es realmente un arte!
Propiedades de la Integral Tipo Arcotangente
Es importante conocer algunas propiedades de la integral tipo arcotangente para poder aplicarlas de manera efectiva. Aquí hay algunas que deberías tener en cuenta:
- Linealidad: La integral de una suma es igual a la suma de las integrales. Esto significa que puedes descomponer integrales más complejas en partes más simples.
- Constantes: Si tienes una constante multiplicando la función que estás integrando, puedes sacarla fuera de la integral.
- Simetría: Las funciones que son simétricas alrededor del eje y pueden simplificar mucho el trabajo de integración.
Consejos para Resolver Integrales Tipo Arcotangente
Ahora que hemos cubierto varios ejemplos, aquí hay algunos consejos para ayudarte a resolver integrales tipo arcotangente con más facilidad:
- Identifica el patrón: Antes de lanzarte a resolver, mira bien la integral y busca patrones que se asemejen a la forma de la integral tipo arcotangente.
- Practica: La práctica hace al maestro. Cuanto más resuelvas, más fácil te resultará identificar cuándo usar esta técnica.
- No temas a los cambios de variable: A veces, un simple cambio de variable puede hacer que una integral difícil se convierta en algo manejable.
Las integrales tipo arcotangente son una herramienta poderosa en el cálculo que te permite abordar problemas de manera más eficiente. A través de ejemplos prácticos y un poco de práctica, puedes dominar esta técnica y aplicarla en diversas situaciones. Recuerda que la clave está en identificar el patrón y no temer a los cambios de variable. ¡Con cada integral que resuelvas, te sentirás más seguro y competente en el fascinante mundo de las matemáticas!
- ¿Qué otros tipos de integrales existen además de la integral tipo arcotangente?
Existen muchos tipos de integrales, como las integrales definidas e indefinidas, integrales por partes y por sustitución, entre otras. Cada una tiene sus propias técnicas y aplicaciones. - ¿Cómo puedo mejorar mis habilidades en cálculo integral?
La mejor manera de mejorar es practicar. Utiliza libros de texto, recursos en línea y ejercicios de práctica. No dudes en buscar ayuda si te sientes atascado. - ¿Las integrales tipo arcotangente son útiles en la vida real?
¡Definitivamente! Se utilizan en campos como la ingeniería, la física y la estadística. Comprender estas integrales puede ayudarte a resolver problemas prácticos en diversas disciplinas.