¿Alguna vez te has preguntado cómo saber si una función está subiendo o bajando en un intervalo determinado? ¡No te preocupes! En este artículo, desglosaremos el concepto de intervalos de crecimiento y decrecimiento de una función, de una manera sencilla y comprensible. Si te has enfrentado a este tema en matemáticas y te has sentido un poco perdido, estás en el lugar adecuado. Imagina que estás en una montaña rusa: hay momentos en que la montaña rusa sube y otros en que baja. Las funciones matemáticas funcionan de manera similar, y es crucial saber en qué partes de la «montaña rusa» estás para entender su comportamiento.
Primero, definamos qué son los intervalos de crecimiento y decrecimiento. Una función está en un intervalo de crecimiento si, a medida que te mueves de izquierda a derecha a lo largo del eje x, los valores de la función (eje y) aumentan. Por otro lado, en un intervalo de decrecimiento, los valores de la función disminuyen. Visualizar esto es fundamental. Cuando graficamos una función, esos intervalos se convierten en tramos de la línea que suben o bajan, como si estuviéramos trazando una ruta en un mapa. Así que, si estás listo, vamos a sumergirnos en este fascinante mundo de funciones matemáticas.
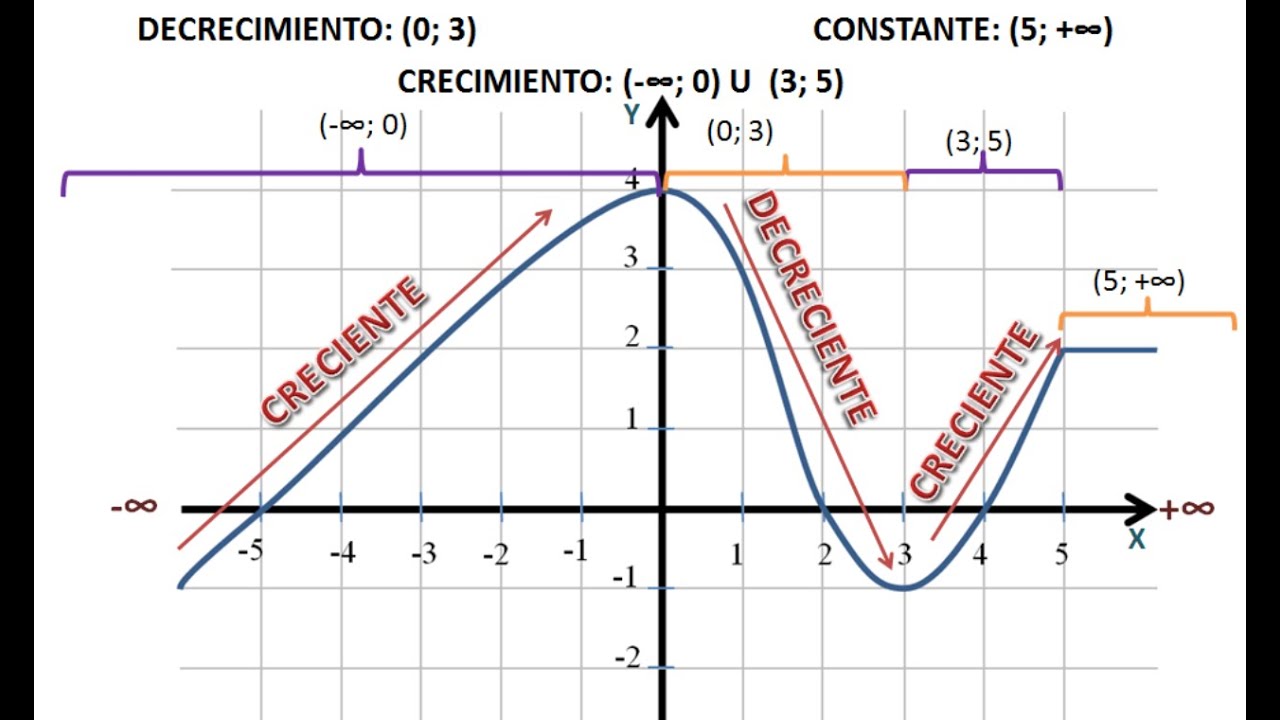
¿Cómo Identificar Intervalos de Crecimiento y Decrecimiento?
Para identificar los intervalos de crecimiento y decrecimiento de una función, necesitamos entender cómo funcionan las derivadas. La derivada de una función nos dice la tasa de cambio de esa función en un punto dado. Si la derivada es positiva, la función está creciendo; si es negativa, la función está decreciendo. Así que, en términos simples, la derivada es como el velocímetro de tu coche. Si el velocímetro marca un número positivo, estás acelerando; si marca un número negativo, estás desacelerando.
Derivadas y su Interpretación
La derivada de una función f(x) se denota como f'(x). Para encontrar los intervalos de crecimiento y decrecimiento, primero calculamos la derivada de la función. Luego, determinamos dónde esta derivada es igual a cero o indefinida. Estos puntos son cruciales porque son los lugares donde la función puede cambiar de comportamiento, como un giro en la montaña rusa.
Por ejemplo, si tienes la función f(x) = x^2, su derivada es f'(x) = 2x. Si igualamos esto a cero, obtenemos x = 0. Este es un punto crítico. Ahora, evaluamos la derivada en los intervalos que se forman a partir de este punto: el intervalo (-∞, 0) y (0, ∞). Si tomamos un número en el primer intervalo, digamos -1, f'(-1) = -2 (negativo), lo que indica que la función está decreciendo. Por otro lado, en el segundo intervalo, tomamos 1, f'(1) = 2 (positivo), lo que indica que la función está creciendo. ¡Y ahí lo tienes! Hemos encontrado los intervalos de crecimiento y decrecimiento.
Graficando para Comprender Mejor
A veces, las matemáticas pueden ser un poco abstractas, así que graficar la función puede ser de gran ayuda. Cuando trazas la función y marcas los puntos críticos que encontraste, podrás visualizar claramente dónde la función sube y baja. Es como ver un paisaje desde un mirador: puedes apreciar mejor las montañas y los valles.
Para nuestra función f(x) = x^2, al graficarla, notarás que forma una parábola. La función decrece hasta el punto (0, 0) y luego comienza a crecer. Este tipo de visualización te permite entender intuitivamente cómo se comporta la función en diferentes intervalos.
Aplicaciones Prácticas de los Intervalos de Crecimiento y Decrecimiento
Conocer los intervalos de crecimiento y decrecimiento no es solo un ejercicio académico; tiene aplicaciones prácticas en diversas áreas. Por ejemplo, en economía, las funciones de costo y beneficio pueden analizarse para determinar cuándo una empresa está creciendo o decreciendo en términos de ganancias. En biología, el crecimiento de poblaciones se puede modelar con funciones que tienen intervalos de crecimiento y decrecimiento.
Ejemplo en Economía
Imagina que tienes una función que representa las ganancias de una empresa: G(x) = -x^2 + 4x. Aquí, x podría representar el número de productos vendidos. Para determinar los intervalos de crecimiento y decrecimiento, primero calculamos la derivada: G'(x) = -2x + 4. Igualamos a cero: -2x + 4 = 0, lo que nos da x = 2. Ahora, evaluamos los intervalos (−∞, 2) y (2, ∞).
Si tomamos un número en el primer intervalo, digamos 1, G'(1) = 2 (positivo), lo que indica que la función está creciendo. En el segundo intervalo, tomamos 3, G'(3) = -2 (negativo), lo que indica que la función está decreciendo. Entonces, podemos concluir que las ganancias de la empresa están en aumento hasta que se venden 2 productos y luego comienzan a disminuir. ¡Esto es información valiosa para la toma de decisiones empresariales!
Ejemplo en Biología
En biología, consideremos el crecimiento de una población de bacterias modelada por la función P(t) = 100e^(0.03t), donde t es el tiempo en horas. Para encontrar los intervalos de crecimiento, calculamos la derivada: P'(t) = 3e^(0.03t). Dado que e^(0.03t) siempre es positivo, sabemos que P'(t) > 0 para cualquier t. Esto significa que la población siempre está creciendo.
Entender estos intervalos puede ayudar a los biólogos a planificar experimentos o a manejar cultivos de manera más efectiva. En este caso, la función no tiene un intervalo de decrecimiento, lo que es una información importante a tener en cuenta.
¿Qué pasa si la derivada es cero en un punto?
Cuando la derivada es cero, significa que la función podría estar en un máximo o mínimo local, o incluso en un punto de inflexión. Es un momento clave para analizar el comportamiento de la función.
¿Es posible que una función no tenga intervalos de decrecimiento?
Sí, algunas funciones pueden ser siempre crecientes, como las funciones exponenciales. Por ejemplo, la función e^x siempre está creciendo y nunca decrece.
¿Qué herramientas puedo usar para graficar funciones?
Existen muchas herramientas disponibles, desde calculadoras gráficas hasta software como Desmos o GeoGebra, que te permiten graficar funciones de manera sencilla.
¿Por qué es importante entender estos conceptos en la vida real?
Entender los intervalos de crecimiento y decrecimiento puede ayudarte a tomar decisiones informadas en diversas áreas, desde negocios hasta ciencias naturales. Te permite anticipar cambios y adaptarte a diferentes situaciones.
¿Cómo puedo practicar más sobre este tema?
Una buena forma de practicar es resolver problemas de cálculo en libros de texto o plataformas en línea. También puedes intentar graficar diferentes funciones y analizar sus intervalos de crecimiento y decrecimiento.
En resumen, los intervalos de crecimiento y decrecimiento son conceptos fundamentales en el estudio de funciones matemáticas. A través de la derivada, podemos descubrir cómo se comporta una función y aplicar este conocimiento a situaciones del mundo real. Ahora que tienes una mejor comprensión de este tema, ¡estás listo para seguir explorando el emocionante mundo de las matemáticas!