¡Hola! Hoy nos adentraremos en el fascinante mundo de la representación gráfica de funciones. ¿Alguna vez te has preguntado cómo una simple ecuación puede transformarse en una imagen visual que nos cuenta una historia? Las gráficas son como mapas que nos guían a través de los números y las relaciones. Imagina que estás en un viaje y cada punto en la gráfica es una parada donde puedes observar y aprender algo nuevo. Vamos a explorar cómo podemos resolver ejercicios y crear gráficos que no solo sean correctos, sino también informativos y atractivos.
¿Qué es una función y por qué es importante representarla gráficamente?
Antes de sumergirnos en los ejercicios, es esencial que entendamos qué es una función. En términos simples, una función es una relación entre un conjunto de entradas (llamadas dominio) y un conjunto de salidas (llamadas codominio). Cada entrada tiene exactamente una salida. ¡Es como una máquina expendedora! Le das una moneda (entrada) y obtienes una bebida (salida). Ahora, ¿por qué es importante graficar estas funciones? Porque al visualizar los datos, podemos identificar patrones, tendencias y comportamientos que podrían no ser obvios solo al mirar números. La gráfica de una función nos permite ver la historia detrás de los números.
Tipos de funciones y sus gráficas
Funciones lineales
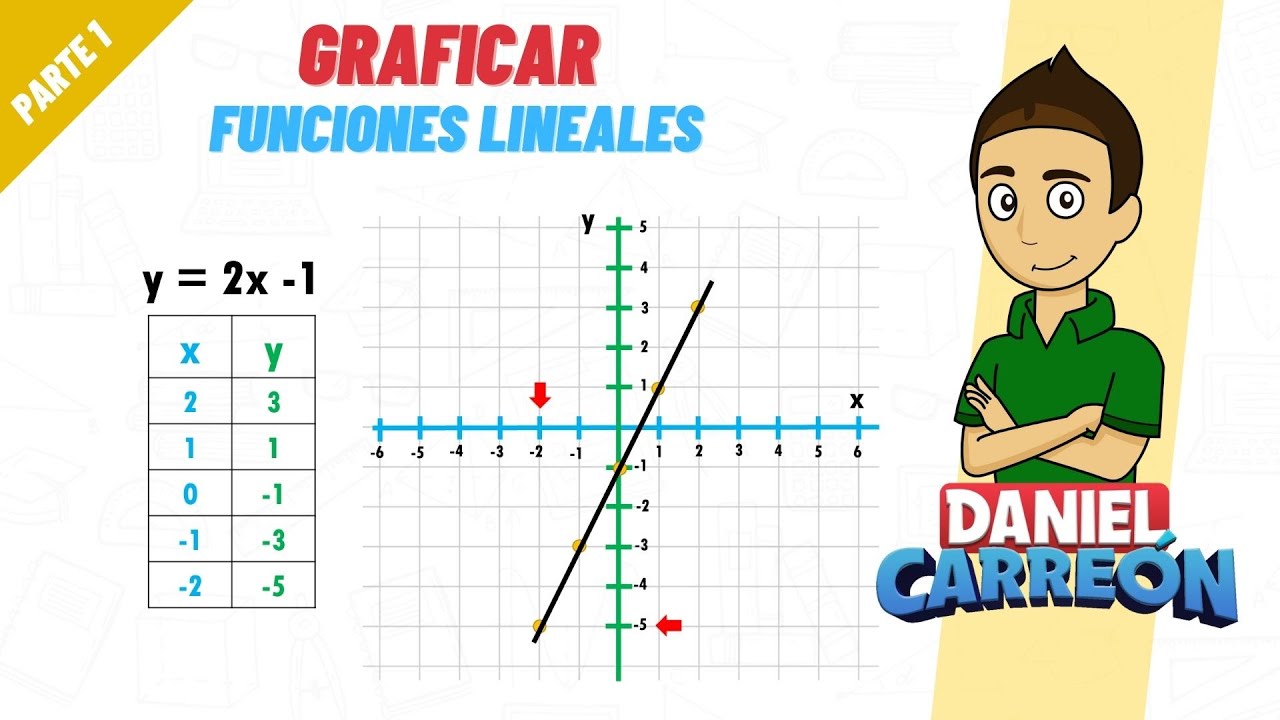
Las funciones lineales son las más sencillas. Tienen la forma y = mx + b, donde m es la pendiente y b es la intersección con el eje y. Imagina que estás dibujando una línea recta en un gráfico. La pendiente te dice cuán empinada es la línea, mientras que la intersección te dice dónde comienza. Vamos a resolver un ejercicio simple: grafiquemos la función y = 2x + 3. Primero, identificamos dos puntos. Si x = 0, entonces y = 3. Si x = 1, entonces y = 5. Con estos puntos, podemos trazar la línea. ¡Y voilà! Ahí tienes una gráfica que muestra cómo cambia y a medida que x aumenta.
Funciones cuadráticas
Ahora, hablemos de las funciones cuadráticas, que tienen la forma y = ax² + bx + c. Estas funciones crean una parábola en la gráfica. Piensa en una sonrisa: eso es lo que ves cuando dibujas una función cuadrática. Por ejemplo, consideremos la función y = x² – 4. Para graficarla, buscamos algunos puntos clave. Si x = -2, entonces y = 0. Si x = 0, entonces y = -4. Si x = 2, también obtenemos y = 0. Al unir estos puntos, formamos una hermosa parábola. ¡No es tan complicado, verdad?
Ejercicios prácticos de representación gráfica
Ejercicio 1: Graficar una función lineal
Vamos a poner manos a la obra. Te reto a graficar la función y = -3x + 1. Primero, elige algunos valores de x. ¿Qué tal -1, 0 y 1? Calculemos:
- Si x = -1, entonces y = 4.
- Si x = 0, entonces y = 1.
- Si x = 1, entonces y = -2.
Ahora que tenemos los puntos (-1, 4), (0, 1) y (1, -2), ¡es hora de graficar! Une esos puntos y observa cómo la línea desciende. ¿Ves cómo la pendiente negativa afecta la dirección de la línea?
Ejercicio 2: Graficar una función cuadrática
Ahora, vamos a graficar una función cuadrática. Te propongo la función y = x² – 1. Nuevamente, elige algunos valores de x. Probar con -2, -1, 0, 1 y 2 sería genial:
- Si x = -2, entonces y = 3.
- Si x = -1, entonces y = 0.
- Si x = 0, entonces y = -1.
- Si x = 1, entonces y = 0.
- Si x = 2, entonces y = 3.
Con estos puntos, (-2, 3), (-1, 0), (0, -1), (1, 0) y (2, 3), puedes dibujar la parábola. ¿No es increíble cómo se forma esa curva perfecta?
Interpretación de gráficas
Identificación de intersecciones
Una vez que tienes tus gráficas, es fundamental saber cómo interpretarlas. Por ejemplo, las intersecciones son cruciales. La intersección con el eje y te dice dónde la función cruza ese eje. En el caso de y = 2x + 3, la intersección es (0, 3). Las intersecciones con el eje x, donde y = 0, son los puntos donde la gráfica toca el eje x. ¿Cómo encontramos estos puntos? Igualamos la función a cero y resolvemos. Para y = x² – 4, esto nos da x² – 4 = 0, lo que nos lleva a x = ±2. ¡Eso significa que la parábola toca el eje x en dos puntos!
Máximos y mínimos
Además de las intersecciones, es esencial identificar los puntos máximos y mínimos. En una función cuadrática, el vértice de la parábola es donde ocurre el máximo o mínimo. Para la función y = x² – 1, el vértice está en (0, -1). Esto significa que la gráfica alcanza su punto más bajo en ese lugar. ¿No es genial? Conocer estos puntos te ayuda a entender el comportamiento de la función.
Ejemplos de funciones más complejas
Funciones exponenciales
Las funciones exponenciales, como y = 2^x, son fascinantes. Crecen muy rápido y tienen una forma característica. Por ejemplo, si graficamos esta función, notamos que para valores negativos de x, y se aproxima a cero, pero nunca lo toca. Es como si estuviera en una carrera, siempre intentando alcanzar la línea de meta pero nunca llegando. Esto es un concepto importante: el comportamiento asintótico.
Funciones trigonométricas
Y no olvidemos las funciones trigonométricas, como y = sin(x) o y = cos(x). Estas funciones son cíclicas y tienen un patrón repetitivo. Al graficarlas, notarás que suben y bajan en un ciclo, como las olas del mar. Si alguna vez has visto una gráfica de sin(x), sabes que tiene un rango entre -1 y 1, lo que significa que nunca sale de esos límites. ¡Es un gran recordatorio de que algunas funciones tienen sus propias reglas!
Consejos para mejorar tus habilidades gráficas
Practica regularmente
La práctica es clave. Cuanto más dibujes gráficas, más cómodo te sentirás. Intenta resolver diferentes tipos de funciones y ver cómo se comportan. No te limites a las funciones básicas; explora las más complejas también. Cuanto más variado sea tu ejercicio, mejor entenderás el concepto general.
Utiliza herramientas gráficas
Hoy en día, hay muchas herramientas en línea que pueden ayudarte a graficar funciones. Puedes usar calculadoras gráficas o software como GeoGebra. Estas herramientas no solo te permiten verificar tus respuestas, sino que también te dan una visualización más clara y precisa de cómo se comporta la función.
¿Cuál es la diferencia entre una función lineal y una cuadrática?
Una función lineal produce una línea recta en su gráfica, mientras que una función cuadrática produce una parábola. Esto se debe a que las funciones cuadráticas incluyen un término cuadrático (como x²), lo que les da esa forma curvada.
¿Cómo puedo saber si una función es creciente o decreciente?
Para determinar si una función es creciente o decreciente, observa la pendiente de la línea en la gráfica. Si la línea sube de izquierda a derecha, la función es creciente. Si baja, es decreciente. En el caso de funciones cuadráticas, si el vértice está en el mínimo, la función es creciente después de ese punto; si está en el máximo, es decreciente.
¿Por qué es útil graficar funciones?
Graficar funciones nos ayuda a visualizar relaciones y comportamientos que podrían ser difíciles de entender solo con números. Nos permite identificar patrones, intersecciones y características clave de la función, lo que es esencial para resolver problemas matemáticos y aplicarlos a situaciones del mundo real.
Así que ahí lo tienes, una guía completa sobre la representación gráfica de funciones. ¡Espero que te haya resultado útil y que ahora te sientas más seguro al enfrentar tus propios ejercicios! Recuerda, la práctica hace al maestro, así que sigue explorando y divirtiéndote con las matemáticas.