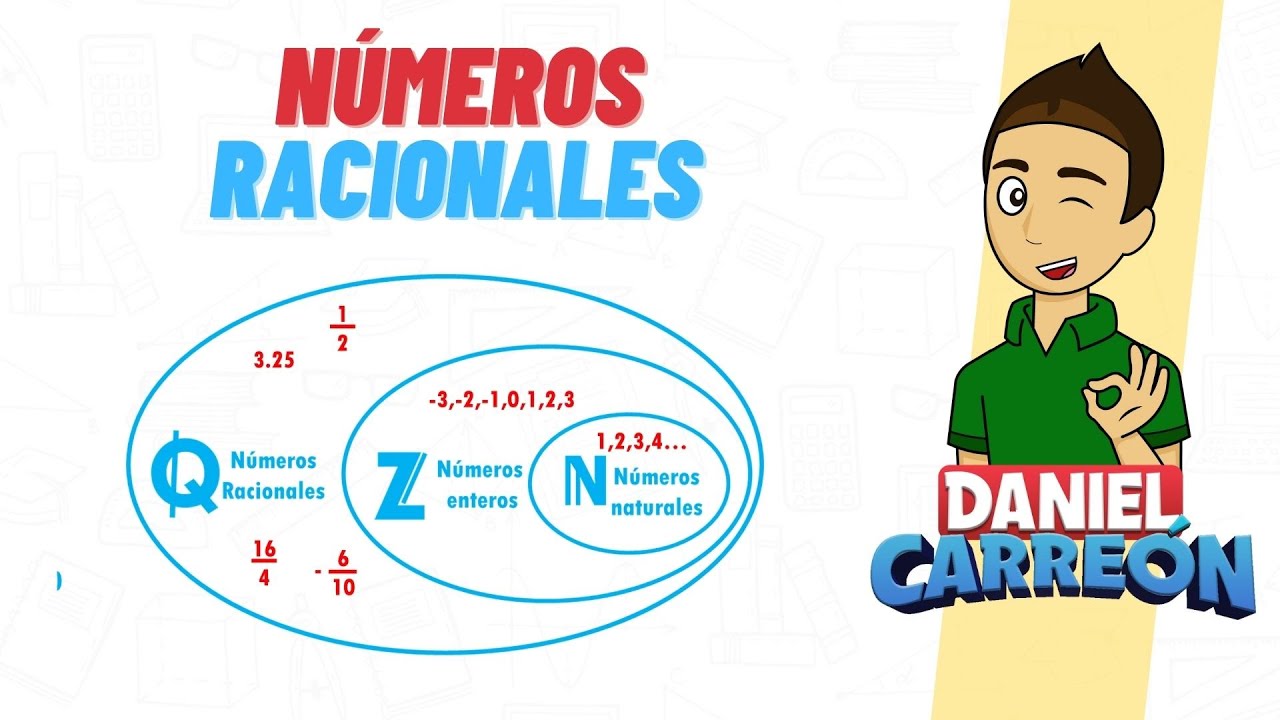
Los números racionales son una parte fundamental de las matemáticas y, en particular, del currículo de 3º de ESO. Pero, ¿qué son exactamente los números racionales? En términos simples, son aquellos números que se pueden expresar como el cociente de dos enteros, donde el denominador no puede ser cero. Esto incluye fracciones, números enteros y decimales finitos o periódicos. Entender los números racionales no solo es esencial para avanzar en matemáticas, sino que también es útil en la vida cotidiana, desde medir ingredientes en una receta hasta calcular descuentos en una tienda. Así que, ¡prepárate! Vamos a sumergirnos en el fascinante mundo de los números racionales a través de ejercicios prácticos y consejos útiles.
### ¿Por qué son importantes los números racionales?
La importancia de los números racionales radica en su omnipresencia. ¿Alguna vez te has preguntado cómo calcular la mitad de una pizza o cómo dividir una cuenta entre amigos? En estos casos, los números racionales son tus mejores amigos. Te permiten hacer operaciones con cantidades que no son enteras y te ayudan a representar situaciones reales. Además, el dominio de los números racionales sienta las bases para conceptos más avanzados en matemáticas, como los números irracionales y el álgebra. Así que, al aprender sobre ellos, no solo estás mejorando tus habilidades matemáticas, sino que también estás preparándote para el futuro.
### Ejercicios Básicos con Números Racionales
Para comenzar, vamos a hacer algunos ejercicios básicos. Estos ejercicios son ideales para familiarizarte con la suma, resta, multiplicación y división de números racionales.
#### Suma de Números Racionales
Ejercicio 1: Suma las siguientes fracciones:
(frac{1}{4} + frac{3}{8})
Solución:
Para sumar fracciones, necesitamos un denominador común. En este caso, el mínimo común múltiplo de 4 y 8 es 8. Convertimos (frac{1}{4}) a (frac{2}{8}). Así que:
(frac{2}{8} + frac{3}{8} = frac{5}{8})
¿Ves lo fácil que es? ¡Practica con más ejemplos y verás cómo te vuelves un experto!
#### Resta de Números Racionales
Ejercicio 2: Resta las siguientes fracciones:
(frac{5}{6} – frac{1}{3})
Solución:
Aquí, el mínimo común múltiplo de 6 y 3 es 6. Convertimos (frac{1}{3}) a (frac{2}{6}):
(frac{5}{6} – frac{2}{6} = frac{3}{6} = frac{1}{2})
Así que, ¡ahí lo tienes! Practica más y te volverás un pro.
### Multiplicación y División de Números Racionales
Ahora que ya sabes sumar y restar, pasemos a la multiplicación y división.
#### Multiplicación de Números Racionales
Ejercicio 3: Multiplica las siguientes fracciones:
(frac{2}{3} times frac{4}{5})
Solución:
Multiplicamos los numeradores y los denominadores:
(2 times 4 = 8) y (3 times 5 = 15)
Así que, (frac{2}{3} times frac{4}{5} = frac{8}{15})
¡Sencillo, ¿verdad? Practica con más ejemplos y te sentirás como un maestro de las fracciones!
#### División de Números Racionales
Ejercicio 4: Divide las siguientes fracciones:
(frac{3}{4} ÷ frac{2}{5})
Solución:
Para dividir fracciones, multiplicamos por el inverso de la segunda fracción:
(frac{3}{4} times frac{5}{2} = frac{15}{8})
Y ahí lo tienes. ¡Sigue practicando y verás cómo te vuelves un experto en fracciones!
### Propiedades de los Números Racionales
Ahora que hemos cubierto las operaciones básicas, hablemos de algunas propiedades interesantes de los números racionales.
#### Propiedad Conmutativa
La propiedad conmutativa dice que el orden de los números no afecta el resultado. Por ejemplo, (a + b = b + a) y (a times b = b times a). Esto significa que puedes sumar o multiplicar en cualquier orden.
#### Propiedad Asociativa
La propiedad asociativa se refiere a cómo agrupamos los números. En suma, ((a + b) + c = a + (b + c)), y en multiplicación, ((a times b) times c = a times (b times c)). ¡Esto es útil para simplificar cálculos!
### Problemas de Aplicación de Números Racionales
Ahora que ya tienes un buen manejo de los números racionales, es hora de poner tus habilidades a prueba con algunos problemas de aplicación.
#### Problema 1: Compras
Si compras 3/4 de kilo de manzanas a 2 euros el kilo, ¿cuánto gastaste?
Solución:
Multiplicamos ( frac{3}{4} times 2 = frac{3}{2} = 1.5) euros. Así que, gastaste 1.5 euros.
#### Problema 2: Recetas
Si una receta requiere 1/3 de taza de azúcar y decides hacer el doble de la receta, ¿cuánto azúcar necesitas?
Solución:
Multiplicamos ( frac{1}{3} times 2 = frac{2}{3}) de taza de azúcar.
### Consejos para Practicar Números Racionales
Practicar es clave para dominar los números racionales. Aquí te dejo algunos consejos:
1. Haz ejercicios variados: No te limites a un solo tipo de operación. Mezcla suma, resta, multiplicación y división.
2. Usa recursos en línea: Hay muchas plataformas y aplicaciones que ofrecen ejercicios interactivos.
3. Forma grupos de estudio: Estudiar con amigos puede hacer que aprender sea más divertido y efectivo.
4. Aplica en la vida real: Intenta encontrar situaciones en tu vida diaria donde puedas usar números racionales.
### Conclusión
Los números racionales son una herramienta poderosa que todos usamos, a menudo sin darnos cuenta. Desde la cocina hasta las finanzas, son parte de nuestra vida cotidiana. Con un poco de práctica y dedicación, dominarás estos conceptos y estarás listo para avanzar a temas más complejos. ¡Así que sigue practicando y no dudes en hacer preguntas si algo no está claro!
### Preguntas Frecuentes
1. ¿Qué son los números racionales?
Los números racionales son aquellos que pueden expresarse como el cociente de dos enteros, donde el denominador no es cero.
2. ¿Por qué son importantes en la vida cotidiana?
Son esenciales para realizar cálculos en situaciones cotidianas como dividir cuentas, medir ingredientes y entender porcentajes.
3. ¿Cómo puedo mejorar en la suma y resta de fracciones?
Practica con ejercicios variados y asegúrate de entender cómo encontrar un denominador común.
4. ¿Qué recursos puedo usar para practicar?
Existen muchas aplicaciones y sitios web que ofrecen ejercicios interactivos y problemas de práctica.
5. ¿Cómo se aplican los números racionales en el álgebra?
Los números racionales son fundamentales en álgebra, ya que muchas ecuaciones y expresiones incluyen fracciones y requieren operaciones con números racionales.
¡Espero que este artículo te haya sido útil y te inspire a seguir explorando el mundo de los números racionales!