¡Hola! Hoy vamos a sumergirnos en un tema que puede sonar un poco complicado al principio, pero te prometo que lo haremos sencillo y divertido. Hablaremos sobre el Mínimo Común Múltiplo, o M.C.M., de un número muy especial: el 3. Pero antes de entrar en detalles, ¿alguna vez te has preguntado por qué es tan importante entender conceptos como el M.C.M.? Bueno, no te preocupes, aquí estamos para desentrañar este misterio juntos. El M.C.M. no es solo un término que se usa en la escuela; es una herramienta fundamental que se utiliza en diversas áreas de la vida diaria, como en la planificación de eventos, la resolución de problemas matemáticos y hasta en la programación de computadoras. Así que, ¡abróchate el cinturón y prepárate para un viaje matemático!
¿Qué es el Mínimo Común Múltiplo?
Primero, vamos a definir qué es el Mínimo Común Múltiplo. En términos simples, el M.C.M. de dos o más números es el número más pequeño que es múltiplo de todos ellos. Pero, ¿qué significa eso realmente? Imagina que tienes varias campanas que suenan en diferentes momentos. El M.C.M. sería el primer momento en el que todas las campanas suenan juntas. ¡Interesante, verdad? Entonces, para nuestro número, el 3, queremos encontrar el múltiplo más pequeño que también se puede dividir por otros números que elegiremos más adelante.
¿Cómo se Calcula el M.C.M.?
Calcular el M.C.M. puede hacerse de varias maneras, pero hoy nos enfocaremos en dos métodos muy comunes: el método de los múltiplos y el método de la factorización. Comencemos con el primero. Para calcular el M.C.M. de 3, podemos listar sus múltiplos. Los primeros múltiplos de 3 son: 3, 6, 9, 12, 15, y así sucesivamente. Si tuviéramos que encontrar el M.C.M. de 3 y 4, por ejemplo, listaríamos los múltiplos de 4: 4, 8, 12, 16, 20. Ahora, ¿cuál es el primer número que aparece en ambas listas? ¡Exacto! Es 12. Así que, el M.C.M. de 3 y 4 es 12.
El Método de la Factorización
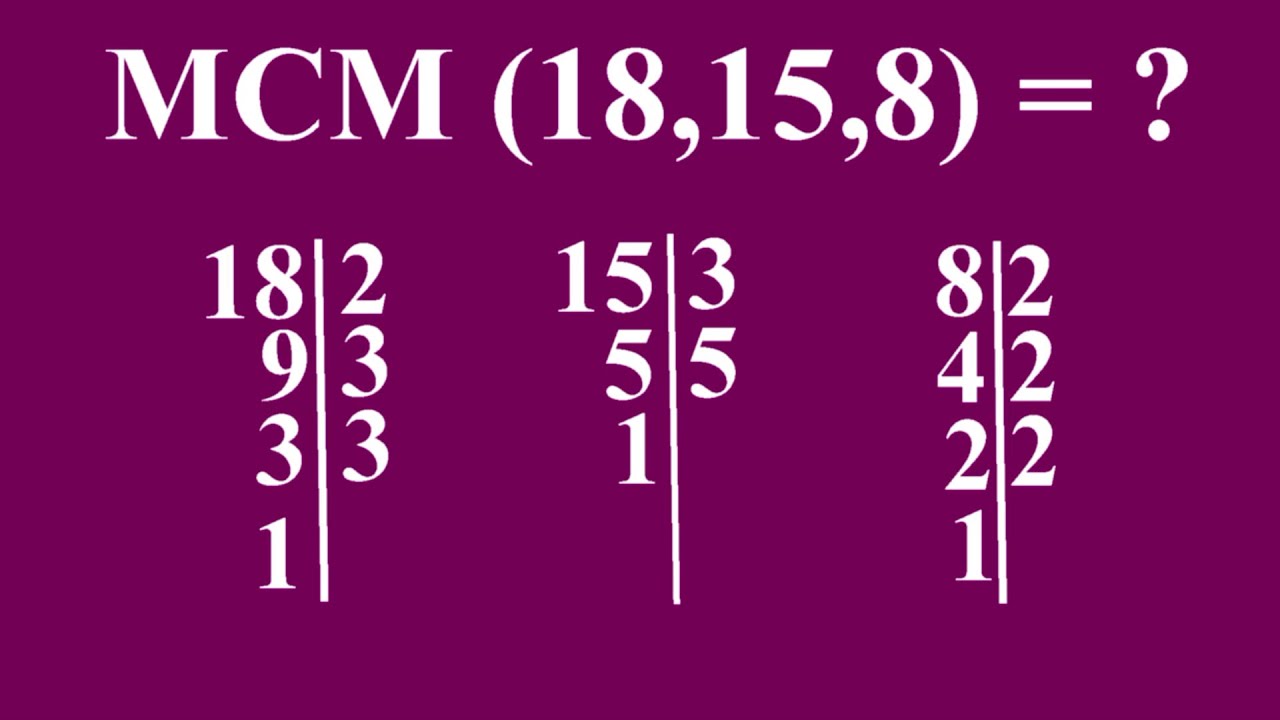
Ahora, hablemos del método de la factorización. Este método puede parecer un poco más técnico, pero es muy útil, especialmente cuando trabajamos con números más grandes. Primero, descomponemos los números en sus factores primos. Para el 3, la única factorización es 3 en sí mismo, ya que es un número primo. Si estuvieras buscando el M.C.M. de 3 y 6, descompondrías 6 en 2 y 3. Luego, tomarías todos los factores primos, asegurándote de incluir cada uno con la mayor potencia que aparece. En este caso, tendrías 2^1 y 3^1, lo que te da 6 como el M.C.M. de 3 y 6.
Ejemplos Prácticos del M.C.M.
Ahora que ya tenemos una idea clara de cómo calcular el M.C.M., vamos a ver algunos ejemplos prácticos. Digamos que queremos organizar una fiesta y tenemos dos grupos de amigos. Uno de ellos llega cada 3 días y el otro cada 4 días. ¿Cuándo será la próxima vez que ambos grupos se encuentren? Para resolver esto, calculamos el M.C.M. de 3 y 4, que ya sabemos que es 12. Esto significa que ambos grupos se reunirán nuevamente en 12 días. ¡Perfecto para planear una gran fiesta!
Aplicaciones del M.C.M. en la Vida Real
El M.C.M. no solo se utiliza en problemas matemáticos. También tiene aplicaciones en situaciones cotidianas. Por ejemplo, si tienes un horario de clases y necesitas coordinar actividades que ocurren en diferentes intervalos de tiempo, el M.C.M. te ayudará a encontrar el momento en que todas las actividades se alinean. Otra situación podría ser cuando estás cocinando y necesitas ajustar las cantidades de ingredientes que requieren diferentes tiempos de cocción. Aquí es donde el M.C.M. brilla, permitiéndote simplificar y organizar tus tareas.
Consejos para Recordar el M.C.M.
Si sientes que calcular el M.C.M. puede ser un poco confuso, aquí tienes algunos consejos que pueden ayudarte. Primero, practica con números pequeños. Cuanto más te familiarices con el proceso, más fácil te resultará. Además, intenta crear tus propias listas de múltiplos. Esto no solo te ayudará a visualizar el concepto, sino que también hará que la práctica sea más divertida. Y recuerda, no tengas miedo de cometer errores. Cada error es una oportunidad de aprendizaje. ¡Así que relájate y disfruta del proceso!
¿Por Qué es Importante el M.C.M.?
Ahora que hemos explorado qué es el M.C.M. y cómo calcularlo, quizás te estés preguntando por qué es tan importante. La verdad es que entender el M.C.M. es crucial para resolver problemas más complejos en matemáticas. Además, es un concepto que se utiliza en muchas áreas, desde la ingeniería hasta la economía. Así que, al dominarlo, no solo mejorarás tus habilidades matemáticas, sino que también te prepararás para enfrentar desafíos más grandes en el futuro.
El Mínimo Común Múltiplo puede parecer un concepto sencillo, pero su aplicación es vasta y esencial en nuestra vida cotidiana. Desde planificar eventos hasta resolver problemas matemáticos complejos, el M.C.M. nos ayuda a organizar y simplificar situaciones. Así que, la próxima vez que te enfrentes a un problema que involucre múltiplos, recuerda que el M.C.M. está ahí para ayudarte. Y lo mejor de todo, ¡no estás solo en esto! Siempre puedes pedir ayuda o buscar recursos adicionales para mejorar tu comprensión. Ahora, ¿qué te parece si practicamos un poco más? ¿Cuáles son tus números favoritos para encontrar el M.C.M.?
¿Cuál es el M.C.M. de 3 y 5?
El M.C.M. de 3 y 5 es 15, ya que es el primer número que aparece en ambas listas de múltiplos.
¿Se puede calcular el M.C.M. de más de dos números?
¡Sí! Puedes calcular el M.C.M. de cualquier cantidad de números. Solo asegúrate de encontrar los múltiplos o descomponer cada número en sus factores primos.
¿El M.C.M. siempre es mayor que los números originales?
No necesariamente. El M.C.M. puede ser igual a uno de los números originales si uno de ellos es múltiplo del otro. Por ejemplo, el M.C.M. de 3 y 6 es 6.
¿Cómo puedo practicar más sobre el M.C.M.?
Existen muchos recursos en línea, como ejercicios y juegos interactivos, que pueden ayudarte a practicar el M.C.M. También puedes crear tus propios problemas y resolverlos.