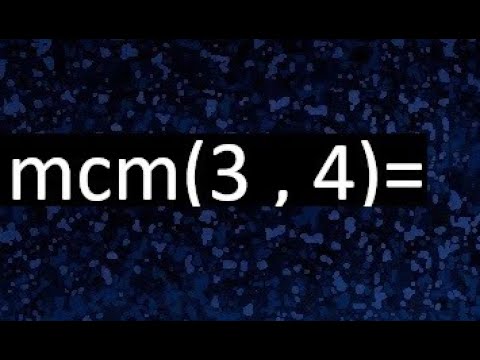¿Qué es el Mínimo Común Múltiplo?
¡Hola! Hoy vamos a hablar sobre algo que puede parecer complicado, pero en realidad es más fácil de lo que piensas: el Mínimo Común Múltiplo, o MCM. ¿Te has preguntado alguna vez cómo puedes encontrar un número que sea múltiplo de dos o más números a la vez? El MCM es precisamente eso. Es el menor número que es múltiplo de todos los números que estamos considerando. En nuestro caso, queremos encontrar el MCM de 3 y 4. Pero antes de entrar en los detalles, vamos a desglosar qué significa ser un múltiplo.
Entendiendo los Múltiplos
Los múltiplos de un número son simplemente los números que puedes obtener al multiplicar ese número por cualquier entero. Por ejemplo, si tomamos el número 3, sus múltiplos serían 3, 6, 9, 12, 15, y así sucesivamente. Por otro lado, los múltiplos de 4 son 4, 8, 12, 16, 20, etc. Ahora, si observas, el MCM de 3 y 4 es el número más pequeño que aparece en ambas listas de múltiplos. ¿Sabes cuál es? ¡Exacto! Es 12. Pero no te preocupes, no nos detendremos aquí. Vamos a explorar cómo llegamos a ese número paso a paso.
Pasos para Calcular el Mínimo Común Múltiplo
Ahora que tenemos una idea básica de lo que son los múltiplos, vamos a ver cómo podemos calcular el MCM de 3 y 4 de una manera sencilla. Existen varios métodos para hacerlo, pero aquí te mostraré dos de los más comunes: el método de listados y el método de descomposición en factores primos.
Método de Listado
Este es probablemente el método más simple. Todo lo que necesitas hacer es listar los múltiplos de ambos números hasta que encuentres el primero que se repita. Vamos a hacerlo juntos:
- Múltiplos de 3: 3, 6, 9, 12, 15, 18, …
- Múltiplos de 4: 4, 8, 12, 16, 20, …
Al mirar ambas listas, puedes ver que el primer número que aparece en ambas es 12. ¡Así que ahí lo tienes! El MCM de 3 y 4 es 12. Este método es genial, pero puede volverse tedioso si los números son más grandes. Entonces, ¿qué hacemos si queremos ser más eficientes?
Método de Descomposición en Factores Primos
Este método puede sonar un poco más complicado, pero en realidad es bastante directo. Consiste en descomponer cada número en sus factores primos y luego multiplicar esos factores para encontrar el MCM. Vamos a hacerlo juntos:
- Descomponemos 3: El único factor primo de 3 es 3 (3 = 3^1).
- Descomponemos 4: Los factores primos de 4 son 2 (4 = 2^2).
Ahora, para encontrar el MCM, tomamos todos los factores primos, usando la mayor potencia de cada uno. En nuestro caso, eso sería:
- 3^1 (de 3)
- 2^2 (de 4)
Entonces, multiplicamos estos factores: 3^1 * 2^2 = 3 * 4 = 12. ¡Y ahí lo tienes de nuevo! El MCM de 3 y 4 es 12. Este método es especialmente útil cuando trabajamos con números más grandes o cuando necesitamos encontrar el MCM de más de dos números.
Ejemplos Prácticos
Ahora que hemos cubierto cómo encontrar el MCM de 3 y 4, ¿por qué no lo aplicamos a algunos ejemplos adicionales? Esto te ayudará a solidificar tu comprensión y ver cómo funciona en diferentes situaciones.
MCM de 6 y 8
Primero, vamos a encontrar el MCM de 6 y 8 usando ambos métodos. Si listamos los múltiplos:
- Múltiplos de 6: 6, 12, 18, 24, …
- Múltiplos de 8: 8, 16, 24, …
El primer múltiplo común es 24. Por lo tanto, el MCM de 6 y 8 es 24.
Ahora, usando el método de descomposición:
- 6 = 2^1 * 3^1
- 8 = 2^3
Tomamos la mayor potencia de cada factor primo: 2^3 y 3^1. Entonces, 2^3 * 3^1 = 8 * 3 = 24. Nuevamente, el MCM es 24. ¡Fácil, verdad?
MCM de 12 y 15
Sigamos con otro ejemplo. Vamos a encontrar el MCM de 12 y 15:
- Múltiplos de 12: 12, 24, 36, 48, …
- Múltiplos de 15: 15, 30, 45, 60, …
El primer múltiplo común aquí es 60. Por lo tanto, el MCM de 12 y 15 es 60.
Ahora, usando la descomposición:
- 12 = 2^2 * 3^1
- 15 = 3^1 * 5^1
Tomamos la mayor potencia de cada factor primo: 2^2, 3^1, y 5^1. Entonces, 2^2 * 3^1 * 5^1 = 4 * 3 * 5 = 60. ¡Listo!
¿Por Qué Es Importante Conocer el MCM?
Ahora que hemos aprendido a calcular el MCM, es posible que te preguntes: «¿Por qué es tan importante conocerlo?» Bueno, el MCM tiene muchas aplicaciones prácticas. Por ejemplo, es fundamental en la resolución de problemas de fracciones, donde necesitamos encontrar un denominador común. También se utiliza en situaciones donde se sincronizan eventos que ocurren en ciclos diferentes, como horarios de trenes o rutinas de clases. Imagina que tienes dos trenes que salen de una estación, uno cada 3 minutos y el otro cada 4 minutos. Si quieres saber cuándo volverán a salir juntos, el MCM te dará esa respuesta.
¿El MCM siempre es mayor que los números originales?
No necesariamente. El MCM de dos números puede ser igual a uno de ellos si uno es un múltiplo del otro. Por ejemplo, el MCM de 4 y 8 es 8.
¿Cómo se relaciona el MCM con el Máximo Común Divisor (MCD)?
El MCM y el MCD son conceptos complementarios. Mientras que el MCM busca el menor múltiplo común, el MCD busca el mayor divisor común. Ambos son útiles en diferentes contextos matemáticos.
¿Se puede encontrar el MCM de más de dos números?
¡Claro! Puedes encontrar el MCM de tres o más números usando el mismo método que mencionamos. Simplemente, descompón cada número en sus factores primos y toma la mayor potencia de cada uno.
¿Hay alguna fórmula para calcular el MCM?
Sí, existe una fórmula que relaciona el MCM y el MCD: MCM(a, b) = (a * b) / MCD(a, b). Esto puede ser útil si ya conoces el MCD.
¿Puedo usar calculadoras para encontrar el MCM?
Absolutamente. Muchas calculadoras científicas y aplicaciones matemáticas tienen funciones para calcular el MCM de manera automática, lo que puede ahorrar tiempo y esfuerzo.
Así que ahí lo tienes, una guía rápida y sencilla para descubrir el Mínimo Común Múltiplo de 3 y 4. Espero que ahora te sientas más seguro al calcular el MCM y que puedas aplicarlo en tus estudios y problemas cotidianos. ¡Hasta la próxima!