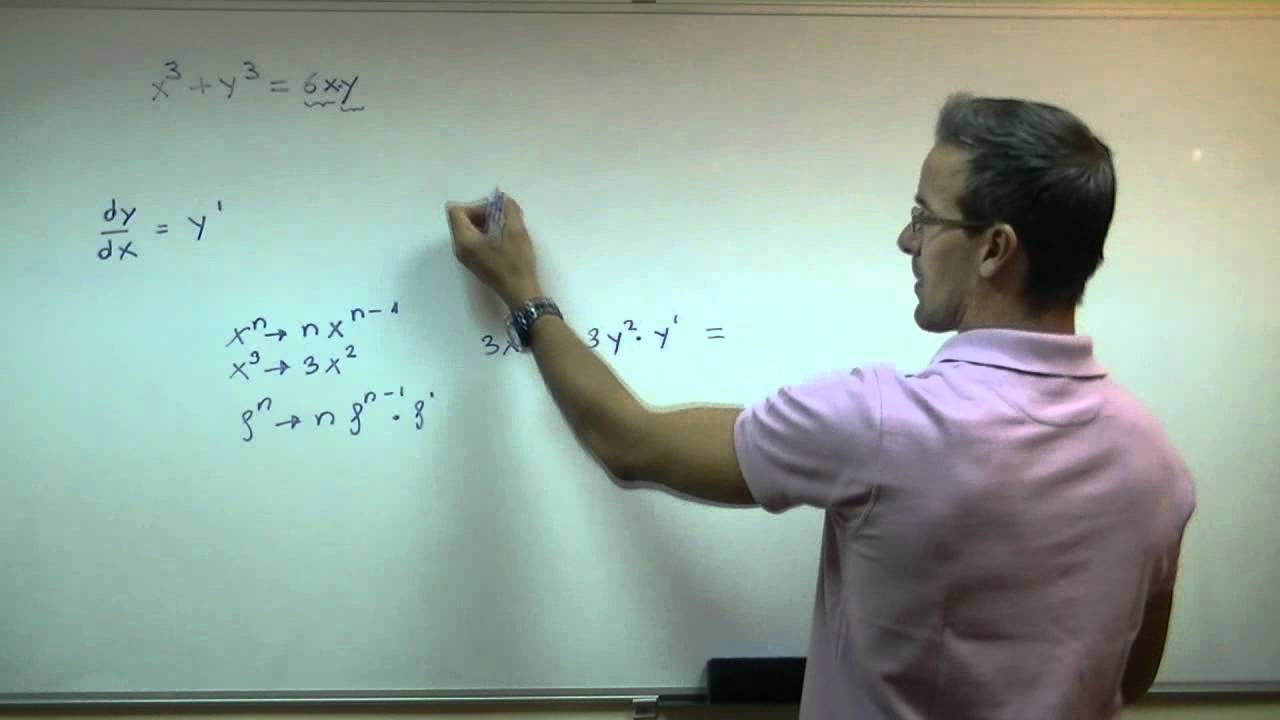¿Qué es la derivada implícita y por qué es importante?
¡Hola! Si alguna vez te has encontrado con una ecuación que parece un laberinto, donde las variables se entrelazan de manera complicada, no te preocupes, no estás solo. En el mundo del cálculo, la derivada implícita es como una brújula que te ayuda a navegar por esas ecuaciones enredadas. ¿Te imaginas tratar de resolver algo como (x^2 + y^2 = 25) para (y)? ¡Es un reto! Aquí es donde la derivada implícita entra en juego, permitiéndonos encontrar la tasa de cambio de (y) respecto a (x) sin necesidad de despejar la variable. En este artículo, exploraremos la derivada implícita a fondo, desde su definición hasta ejemplos prácticos que te harán sentir como un experto. ¡Así que prepárate para sumergirte en el fascinante mundo de las matemáticas!
¿Qué es la derivada implícita?
La derivada implícita se refiere a un método para calcular la derivada de una función cuando no está expresada de forma explícita. En otras palabras, cuando tienes una relación entre (x) y (y) que no se puede escribir fácilmente como (y = f(x)), la derivada implícita te permite obtener (frac{dy}{dx}) sin tener que despejar (y). Imagina que estás en una fiesta y todos están bailando, pero tú no puedes ver a todos los que están allí. Así es como funciona la derivada implícita: puedes obtener información sobre todos sin necesidad de tener una vista clara de cada uno.
La regla de la cadena en la derivada implícita
Cuando trabajamos con derivadas implícitas, la regla de la cadena es nuestra mejor amiga. La regla de la cadena nos dice que si tienes una función compuesta, puedes derivar la función exterior y multiplicarla por la derivada de la función interior. En el caso de la derivada implícita, cuando derivamos términos que involucran (y), debemos recordar multiplicar por (frac{dy}{dx}). Por ejemplo, si tenemos la ecuación (x^2 + y^2 = 25) y la derivamos, obtenemos:
(2x + 2yfrac{dy}{dx} = 0)
Esto significa que debemos ser cuidadosos al tratar con (y) en nuestras derivadas. ¡Es como bailar salsa! Tienes que seguir el ritmo y no perder el paso para no tropezar.
Ejemplo 1: Derivada implícita de una circunferencia
Comencemos con un ejemplo clásico: la ecuación de una circunferencia. Supongamos que tenemos la ecuación:
(x^2 + y^2 = 25)
Queremos encontrar (frac{dy}{dx}). Derivamos ambos lados de la ecuación respecto a (x):
2x + 2yfrac{dy}{dx} = 0
Ahora, despejamos (frac{dy}{dx}):
2yfrac{dy}{dx} = -2x
frac{dy}{dx} = -frac{x}{y}
Y ahí lo tienes. La derivada implícita nos ha dado la tasa de cambio de (y) respecto a (x) sin tener que despejar (y). ¡Fácil, verdad? Pero, ¿qué pasa si la ecuación es más complicada?
Ejemplo 2: Derivada implícita en una curva más compleja
Ahora, probemos algo un poco más complicado. Considera la ecuación:
(x^3 + y^3 = 6xy)
Vamos a derivar ambos lados de la ecuación. Aplicamos la regla de la cadena y la regla del producto:
3x^2 + 3y^2frac{dy}{dx} = 6left(y + xfrac{dy}{dx}right)
Esto se simplifica a:
3x^2 + 3y^2frac{dy}{dx} = 6y + 6xfrac{dy}{dx}
Ahora, agrupamos los términos que contienen (frac{dy}{dx}):
3y^2frac{dy}{dx} - 6xfrac{dy}{dx} = 6y - 3x^2
Factorizamos (frac{dy}{dx}):
frac{dy}{dx}(3y^2 - 6x) = 6y - 3x^2
Finalmente, despejamos (frac{dy}{dx}):
frac{dy}{dx} = frac{6y - 3x^2}{3y^2 - 6x}
¡Y ahí lo tienes! Hemos encontrado la derivada implícita de una relación más complicada. A veces, resolver estas ecuaciones puede parecer un rompecabezas, pero con paciencia y práctica, te convertirás en un experto.
Ejemplo 3: Aplicaciones de la derivada implícita
Las derivadas implícitas no solo son útiles para encontrar tasas de cambio, sino que también tienen aplicaciones en problemas del mundo real. Por ejemplo, imagina que eres un arquitecto y estás diseñando un edificio. La forma del edificio puede estar representada por una ecuación implícita. Si necesitas conocer cómo cambiará la altura del edificio respecto a su base cuando se ajuste un diseño, la derivada implícita te ayudará a calcular eso. ¡Es como tener una herramienta mágica que te da información valiosa!
Ejercicio práctico
Ahora que hemos visto algunos ejemplos, es tu turno. Intenta resolver la siguiente ecuación:
(x^2y + y^2 = 10)
Deriva ambos lados de la ecuación y encuentra (frac{dy}{dx}). No te preocupes si te sientes un poco perdido; la práctica es clave para dominar este concepto.
Consejos para resolver derivadas implícitas
Si bien la derivada implícita puede parecer un desafío al principio, aquí hay algunos consejos que te ayudarán a resolver problemas con mayor facilidad:
- Practica regularmente: Cuanto más practiques, más cómodo te sentirás con el proceso.
- Descompón los problemas: No trates de resolver todo de una vez. Tómate tu tiempo para desglosar cada parte de la ecuación.
- Revisa tus reglas: Asegúrate de tener claras las reglas de derivación, como la regla de la cadena y la regla del producto.
- Utiliza ejemplos: Aprender a través de ejemplos te ayudará a ver cómo se aplican las derivadas implícitas en diferentes situaciones.
¿Qué debo hacer si no puedo despejar (y) de la ecuación?
No te preocupes, la derivada implícita fue creada precisamente para situaciones como esa. Puedes seguir derivando sin despejar (y) y obtener (frac{dy}{dx}) directamente.
¿La derivada implícita es solo para funciones de dos variables?
¡No! Aunque comúnmente se utiliza para funciones de dos variables, también puedes aplicar la derivada implícita a ecuaciones con más variables. Solo debes seguir el mismo proceso de derivación.
¿Existen otras aplicaciones de la derivada implícita en matemáticas?
Definitivamente. La derivada implícita es fundamental en campos como la geometría, la física y la economía, donde las relaciones entre variables no siempre son directas.
¿Es difícil aprender a usar la derivada implícita?
Como todo en matemáticas, puede ser un poco complicado al principio. Pero con práctica y paciencia, se convierte en una herramienta poderosa y útil. ¡No te rindas!
¿Puedo usar software para resolver derivadas implícitas?
Sí, hay varios programas y calculadoras que pueden ayudarte a resolver derivadas implícitas. Sin embargo, es recomendable entender el proceso manualmente para que puedas aplicar el conocimiento cuando sea necesario.
Recuerda que la clave para dominar la derivada implícita es la práctica constante y la curiosidad. Así que, ¡manos a la obra y a resolver ecuaciones!