Entendiendo el Comportamiento de las Funciones
¿Alguna vez te has preguntado cómo saber si una función está subiendo o bajando? ¡Es una gran pregunta! Comprender los intervalos de crecimiento y decrecimiento es fundamental en el estudio de las matemáticas, especialmente cuando se trata de funciones. Imagina que estás escalando una montaña. A veces subes, a veces bajas. Así es como funcionan las funciones en matemáticas. Al identificar estos intervalos, no solo puedes entender mejor la función, sino que también puedes aplicar este conocimiento a problemas del mundo real, como optimización, economía y ciencias.
En este artículo, vamos a desglosar el concepto de intervalos de crecimiento y decrecimiento. Veremos qué son, cómo identificarlos y por qué son importantes. Usaremos ejemplos prácticos y gráficos para hacerlo más fácil. Así que, si estás listo, ¡comencemos!
¿Qué son los Intervalos de Crecimiento y Decrecimiento?
Los intervalos de crecimiento y decrecimiento son partes de una función donde esta aumenta o disminuye. Para entenderlo mejor, piensa en una montaña rusa. Cuando sube, la función está en un intervalo de crecimiento, y cuando baja, está en un intervalo de decrecimiento. Es sencillo, ¿verdad?
Matemáticamente, si tienes una función f(x), decimos que está creciendo en un intervalo [a, b] si para cualquier par de puntos x1 y x2 en ese intervalo, donde x1 < x2, se cumple que f(x1) < f(x2). Por otro lado, la función está decreciendo en un intervalo si f(x1) > f(x2). Entonces, lo que necesitamos hacer es analizar la derivada de la función, porque la derivada nos dice la tasa de cambio de la función.
La Derivada y su Importancia
La derivada es como un radar que nos ayuda a detectar si la función está subiendo o bajando. Si la derivada de f(x) es positiva en un intervalo, eso significa que la función está creciendo. Por el contrario, si la derivada es negativa, la función está decreciendo. Y si la derivada es cero, podría ser un punto crítico, lo que significa que podríamos tener un máximo o mínimo local.
Entonces, la clave aquí es calcular la derivada y analizar su signo en diferentes intervalos. ¡No te preocupes! No es tan complicado como parece.
Pasos para Identificar los Intervalos de Crecimiento y Decrecimiento
Ahora que sabemos qué son los intervalos de crecimiento y decrecimiento, veamos cómo podemos identificarlos paso a paso.
Paso 1: Encuentra la Derivada de la Función
Comencemos con un ejemplo. Supongamos que tienes la función f(x) = x^3 – 3x^2 + 4. El primer paso es encontrar su derivada. Para esto, aplicamos la regla de potencia:
f'(x) = 3x^2 – 6x.
¡Listo! Ahora tenemos la derivada.
Paso 2: Encuentra los Puntos Críticos
Los puntos críticos son donde la derivada es cero o no está definida. Para encontrar estos puntos, igualamos la derivada a cero:
3x^2 – 6x = 0.
Factorizamos:
3x(x – 2) = 0.
De aquí, obtenemos dos puntos críticos: x = 0 y x = 2.
Paso 3: Analiza el Signo de la Derivada
Ahora, necesitamos analizar el signo de la derivada en los intervalos que se forman alrededor de los puntos críticos. Los intervalos son (-∞, 0), (0, 2) y (2, ∞). Escogemos un valor de prueba en cada intervalo:
– Para el intervalo (-∞, 0), elijamos x = -1: f'(-1) = 3(-1)^2 – 6(-1) = 3 + 6 = 9 (positivo).
– Para el intervalo (0, 2), elijamos x = 1: f'(1) = 3(1)^2 – 6(1) = 3 – 6 = -3 (negativo).
– Para el intervalo (2, ∞), elijamos x = 3: f'(3) = 3(3)^2 – 6(3) = 27 – 18 = 9 (positivo).
Paso 4: Conclusiones sobre los Intervalos
Con esta información, podemos concluir que:
– La función está creciendo en los intervalos (-∞, 0) y (2, ∞).
– La función está decreciendo en el intervalo (0, 2).
Es así de sencillo. Ahora tienes una herramienta poderosa para analizar cualquier función que te encuentres.
Ejemplo Adicional: Funciones Trigonométricas
Ahora, vamos a ver un ejemplo más complicado, esta vez usando una función trigonométrica. Consideremos f(x) = sin(x). La derivada de esta función es f'(x) = cos(x).
Identificando Intervalos en Funciones Trigonométricas
Para identificar los intervalos de crecimiento y decrecimiento, necesitamos encontrar dónde cos(x) es positivo o negativo. Recordemos que cos(x) es positivo en los intervalos:
– (2nπ, (2n+1)π) donde n es un número entero (los cuartos del primer y cuarto cuadrante).
Y cos(x) es negativo en:
– ((2n+1)π, (2n+2)π) donde n es un número entero (los cuartos del segundo y tercer cuadrante).
Por lo tanto, podemos concluir que:
– f(x) = sin(x) está creciendo en los intervalos (2nπ, (2n+1)π).
– f(x) = sin(x) está decreciendo en ((2n+1)π, (2n+2)π).
¡Eso es un poco más complejo, pero aún manejable!
Aplicaciones Prácticas de los Intervalos de Crecimiento y Decrecimiento
Entender los intervalos de crecimiento y decrecimiento no es solo un ejercicio académico. Tiene aplicaciones prácticas en diversas áreas. Por ejemplo, en economía, puedes usar estos conceptos para analizar costos y beneficios, maximizar ganancias o minimizar pérdidas. En física, puedes estudiar el movimiento de objetos, determinando cuándo están acelerando o desacelerando.
Además, en biología, puedes modelar poblaciones de organismos, entendiendo en qué condiciones estas crecen o decrecen. ¡Las posibilidades son infinitas!
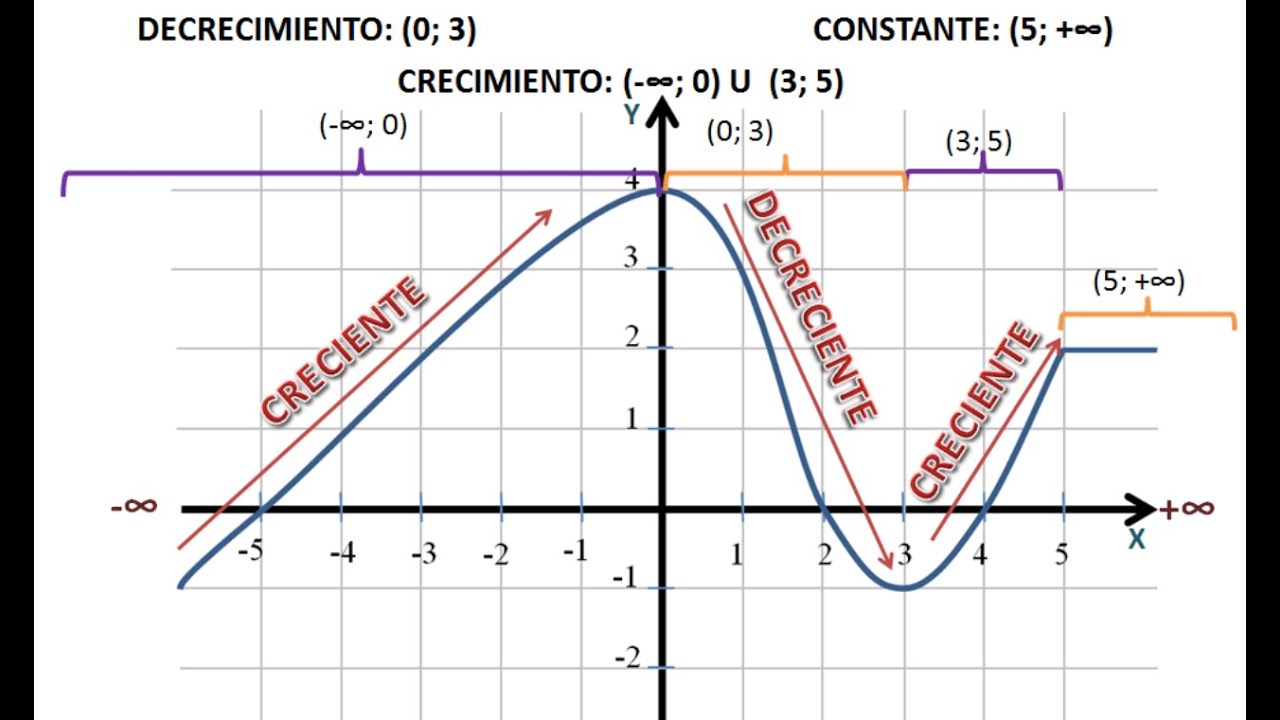
Visualizando Gráficamente
Una de las mejores maneras de entender los intervalos de crecimiento y decrecimiento es a través de gráficos. Al graficar la función, puedes ver visualmente dónde la función sube y baja. Si tienes acceso a herramientas gráficas, prueba graficar las funciones que hemos discutido y observa los intervalos que hemos encontrado.
¿Es necesario calcular la derivada para identificar los intervalos?
No es estrictamente necesario, pero calcular la derivada es la forma más efectiva de identificar los intervalos de crecimiento y decrecimiento de manera precisa. Sin la derivada, es difícil saber cómo se comporta la función.
¿Qué sucede si la derivada nunca es cero?
Si la derivada nunca es cero, significa que la función es monótona en todo su dominio, es decir, siempre está creciendo o siempre está decreciendo.
¿Los intervalos de crecimiento y decrecimiento son siempre continuos?
No necesariamente. Puedes tener funciones que crecen y decrecen en intervalos separados. Por ejemplo, funciones a trozos pueden tener diferentes comportamientos en diferentes partes.
¿Cómo se relacionan los intervalos de crecimiento con los máximos y mínimos?
Los puntos donde la derivada es cero son candidatos a ser máximos o mínimos locales. Un intervalo de crecimiento se convierte en un intervalo de decrecimiento en estos puntos críticos, lo que indica un cambio en la dirección de la función.
¿Se pueden aplicar estos conceptos a funciones no polinómicas?
¡Absolutamente! Los conceptos de crecimiento y decrecimiento se aplican a una variedad de funciones, incluyendo exponenciales, logarítmicas y trigonométricas.
Identificar los intervalos de crecimiento y decrecimiento es una herramienta valiosa en el arsenal de cualquier estudiante de matemáticas. No solo ayuda a comprender el comportamiento de las funciones, sino que también permite aplicar este conocimiento a situaciones del mundo real. Ya sea que estés resolviendo un problema de optimización o analizando datos, esta habilidad te será de gran utilidad. Así que, la próxima vez que te enfrentes a una función, recuerda que puedes desglosarla y entender cómo se comporta. ¡Buena suerte!