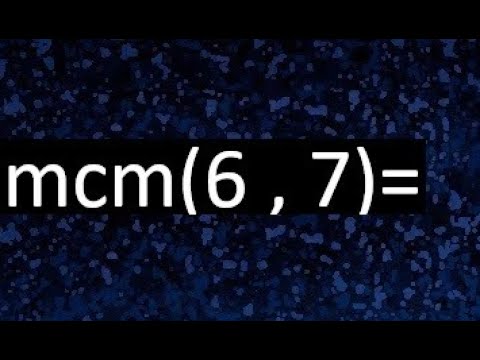¿Te has preguntado alguna vez cómo se relacionan los números entre sí? Imagina que tienes un grupo de amigos que quieren organizar una fiesta, pero cada uno tiene una idea diferente sobre cuándo debe ser. Algunos quieren el evento cada 6 días, mientras que otros prefieren cada 7 días. ¿Cómo puedes encontrar el mejor día para que todos se reúnan? Aquí es donde entra en juego el concepto de Mínimo Común Múltiplo (MCM). En este artículo, te guiaré a través del proceso de calcular el MCM de 6 y 7, paso a paso, para que puedas entenderlo a fondo.
El Mínimo Común Múltiplo es, básicamente, el número más pequeño que es múltiplo de dos o más números. En nuestro caso, buscamos el MCM de 6 y 7. Pero antes de entrar en detalles, vamos a desglosar el proceso y a familiarizarnos con algunos términos que pueden sonar complicados, pero que en realidad son bastante sencillos. ¡Vamos a ello!
¿Qué es el Mínimo Común Múltiplo?
Para empezar, es fundamental entender qué significa Mínimo Común Múltiplo. Si tomamos dos números, el MCM es el número más pequeño que se puede dividir sin dejar residuo por ambos números. Esto es como buscar un punto de encuentro en una pista de baile, donde todos puedan moverse al mismo ritmo.
Por ejemplo, si consideramos el número 6, sus múltiplos son 6, 12, 18, 24, 30, y así sucesivamente. Para el número 7, los múltiplos son 7, 14, 21, 28, 35, etc. El MCM de 6 y 7 será el primer número que aparece en ambas listas de múltiplos. Pero, ¿cómo encontramos ese número?
Métodos para Calcular el Mínimo Común Múltiplo
Hay varios métodos que puedes usar para calcular el MCM. Aquí te explicaré dos de los más comunes: el método de los múltiplos y el método de la factorización prima. Ambos son efectivos, pero cada uno tiene su propia manera de funcionar.
Método de los Múltiplos
Este método es bastante intuitivo. Simplemente, generamos los múltiplos de ambos números hasta que encontramos el primero que coincide. Vamos a hacerlo juntos:
1. Multiplicamos el número 6:
– 6 x 1 = 6
– 6 x 2 = 12
– 6 x 3 = 18
– 6 x 4 = 24
– 6 x 5 = 30
– 6 x 6 = 36
Así que los múltiplos de 6 son: 6, 12, 18, 24, 30, 36, …
2. Multiplicamos el número 7:
– 7 x 1 = 7
– 7 x 2 = 14
– 7 x 3 = 21
– 7 x 4 = 28
– 7 x 5 = 35
– 7 x 6 = 42
Así que los múltiplos de 7 son: 7, 14, 21, 28, 35, 42, …
3. Buscamos el primer múltiplo común:
Observamos las listas y notamos que el número 42 es el primer múltiplo que aparece en ambas listas. Por lo tanto, el MCM de 6 y 7 es 42.
Método de la Factorización Prima
Ahora, vamos a explorar el método de la factorización prima. Este método puede parecer un poco más complicado al principio, pero es extremadamente útil, especialmente cuando trabajamos con números más grandes.
1. Factorizamos cada número en sus factores primos:
– Para el 6: 6 = 2 x 3
– Para el 7: 7 es un número primo, así que se queda como 7.
2. Tomamos todos los factores primos:
Debemos tomar cada factor primo el mayor número de veces que aparece en cualquiera de las factorizaciones. En este caso:
– 2 aparece 1 vez (de 6)
– 3 aparece 1 vez (de 6)
– 7 aparece 1 vez (de 7)
3. Multiplicamos estos factores:
Así que multiplicamos: 2 x 3 x 7 = 42.
Y voilà, hemos llegado al mismo resultado: el MCM de 6 y 7 es 42.
Aplicaciones del Mínimo Común Múltiplo
Ahora que hemos aprendido a calcular el MCM, es interesante ver en qué situaciones lo podemos aplicar en la vida real. ¿Alguna vez has intentado coordinar horarios? El MCM puede ayudarte a encontrar momentos en los que diferentes eventos se alinean.
Por ejemplo, si tienes dos alarmas que suenan cada 6 y 7 minutos, el MCM te dirá cada cuántos minutos ambas alarmas sonarán juntas. Esto es muy útil cuando se trata de planificar actividades, organizar tareas o incluso en la programación de eventos.
Ejemplos Prácticos
Imagina que estás organizando un torneo de videojuegos. Algunos jugadores quieren jugar cada 6 días, mientras que otros prefieren cada 7 días. Si quieres que todos jueguen el mismo día, ¿cuándo debería ser? Aquí es donde calculas el MCM. Con el MCM de 6 y 7, sabes que el torneo se puede programar cada 42 días para que todos participen.
Otro ejemplo sería en la cocina. Supón que tienes dos recetas que requieren que pongas un ingrediente especial cada 6 y 7 minutos. Al calcular el MCM, puedes planificar el momento perfecto para añadir ese ingrediente sin que se te pase.
Errores Comunes al Calcular el Mínimo Común Múltiplo
Aunque calcular el MCM puede parecer sencillo, hay algunos errores comunes que las personas suelen cometer. Aquí te dejo algunos consejos para evitarlos:
1. Confundir MCM con MCD:
El Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) son conceptos diferentes. Asegúrate de saber cuál estás buscando.
2. Olvidar los múltiplos:
Cuando usas el método de los múltiplos, asegúrate de no omitir ningún número. Es fácil saltarse un múltiplo y perderse el MCM.
3. No considerar los números primos:
En la factorización prima, asegúrate de incluir todos los factores primos, incluso si aparecen solo una vez.
Calcular el Mínimo Común Múltiplo de 6 y 7 es un proceso que puede parecer complicado al principio, pero con un poco de práctica, se convierte en algo bastante sencillo. Ya sea que utilices el método de los múltiplos o la factorización prima, lo importante es entender el concepto y cómo aplicarlo a situaciones de la vida real.
Recuerda, el MCM no solo es una herramienta matemática, sino que también puede ayudarte a coordinar eventos, planificar actividades y optimizar tu tiempo. Así que la próxima vez que te encuentres con números y necesites encontrar un punto en común, ¡no dudes en usar el MCM!
¿Cuál es la diferencia entre MCM y MCD?
El Mínimo Común Múltiplo (MCM) es el número más pequeño que es múltiplo de dos o más números, mientras que el Máximo Común Divisor (MCD) es el número más grande que divide a dos o más números sin dejar residuo.
¿El MCM siempre es mayor que los números originales?
No necesariamente. El MCM de dos números puede ser igual a uno de ellos, pero en la mayoría de los casos, será mayor. Por ejemplo, el MCM de 1 y cualquier número es siempre ese número.
¿Puedo calcular el MCM de más de dos números?
Sí, puedes calcular el MCM de más de dos números utilizando el mismo método. Simplemente calcula el MCM de dos números a la vez hasta que incluyas todos los números.
¿Qué hago si uno de los números es cero?
El MCM de cualquier número y cero no está definido, ya que no hay múltiplos de cero. En este caso, es mejor evitar el cálculo.
¿Por qué es importante el MCM en la vida diaria?
El MCM es útil para coordinar horarios, planificar actividades y optimizar procesos. Nos ayuda a encontrar momentos en los que diferentes eventos se alinean, facilitando la organización y la gestión del tiempo.
¡Espero que esta guía te haya sido útil y que ahora te sientas más cómodo calculando el Mínimo Común Múltiplo!