Las funciones son uno de esos conceptos que, a menudo, parecen intimidantes al principio, pero que en realidad son fundamentales para entender no solo las matemáticas, sino también muchas disciplinas científicas y tecnológicas. Imagina que las funciones son como máquinas que toman un input, lo procesan y devuelven un output. En este artículo, vamos a desglosar las características de las funciones, explorando por qué son tan importantes y cómo pueden aplicarse en la vida diaria. Así que, si alguna vez te has preguntado qué es una función o por qué deberías preocuparte por ellas, sigue leyendo. ¡Vamos a sumergirnos!
¿Qué es una Función?
En términos simples, una función es una relación matemática que asigna a cada elemento de un conjunto (llamado dominio) un único elemento de otro conjunto (llamado codominio). Piensa en ello como un amoroso chef que toma ingredientes específicos (inputs) y los transforma en un plato delicioso (output). Cada vez que le das los mismos ingredientes, obtendrás el mismo plato. Esta propiedad es lo que hace que las funciones sean tan predecibles y útiles en matemáticas y otras áreas.
Características Clave de las Funciones
Unicidad del Output
Una de las características más esenciales de las funciones es que, por cada valor de entrada, hay un solo valor de salida. Si alguna vez has jugado a un juego de adivinanza, entenderás esta idea. Si el jugador A dice «3», el resultado es «9». Si vuelve a decir «3», el resultado sigue siendo «9». No importa cuántas veces lo intente, el resultado no cambiará. Esta unicidad es lo que permite que las funciones sean predecibles y utilizables en cálculos matemáticos.
Dominio y Codominio
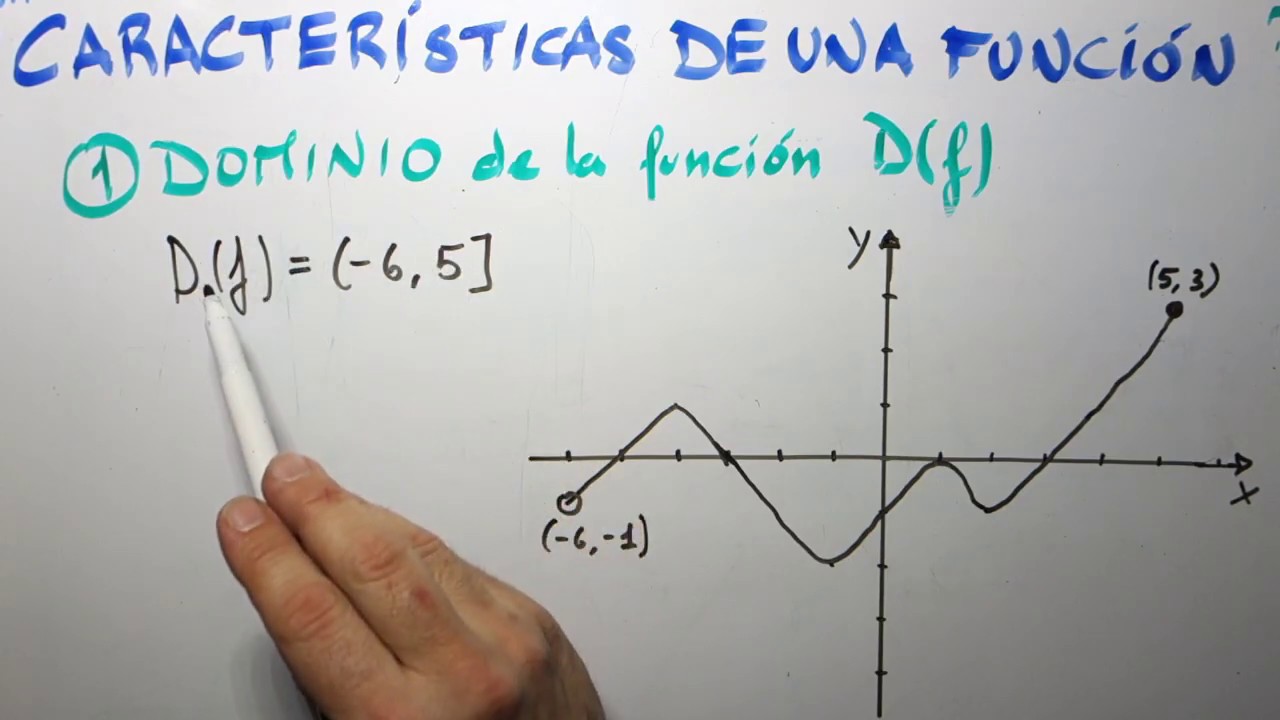
Cada función tiene un dominio, que es el conjunto de todos los posibles inputs, y un codominio, que es el conjunto de posibles outputs. Imagina que el dominio es un jardín lleno de diferentes tipos de flores y el codominio es una hermosa exhibición de ramos. No todas las flores pueden convertirse en ramos; algunas simplemente no encajan. Conocer el dominio y el codominio de una función es crucial para entender cómo se comporta y qué resultados puedes esperar.
Representación Gráfica
Las funciones pueden representarse gráficamente, lo que facilita su comprensión. Piensa en un gráfico como un mapa del tesoro. Cada punto en el gráfico representa un par de valores: uno del dominio y otro del codominio. Al observar el gráfico, puedes ver patrones y tendencias que de otro modo podrían ser difíciles de captar. Además, algunas funciones son tan famosas que tienen gráficos icónicos, como la parábola de la función cuadrática o la línea recta de una función lineal.
Tipos de Funciones
Funciones Lineales
Las funciones lineales son quizás las más simples y conocidas. Tienen la forma y = mx + b, donde m es la pendiente y b es la intersección con el eje y. Piensa en ellas como una carretera recta: siempre avanzas en la misma dirección, y la relación entre x e y es constante. Estas funciones son útiles en muchas situaciones cotidianas, desde calcular el costo de una compra hasta determinar el tiempo de viaje.
Funciones Cuadráticas
Las funciones cuadráticas, que tienen la forma y = ax^2 + bx + c, son un poco más complejas. Su gráfico forma una parábola. Imagina que lanzas una pelota al aire: al principio, sube y luego baja. Esa trayectoria es una función cuadrática. Estas funciones son esenciales en física y otras ciencias, donde el movimiento y la aceleración son factores clave.
Funciones Exponenciales
Las funciones exponenciales crecen o decrecen a un ritmo sorprendente. Tienen la forma y = a * b^x, donde b es la base de la exponencial. Imagina que estás en un juego donde tus puntos se duplican cada vez que ganas; eso es una función exponencial en acción. Estas funciones son comunes en el crecimiento poblacional, la economía y muchas otras áreas donde el cambio es rápido y dramático.
¿Por qué son Importantes las Funciones?
Ahora que hemos explorado las características y tipos de funciones, es natural preguntarse: ¿por qué son tan importantes? La respuesta es simple: las funciones son la base de la modelización matemática. Sin ellas, sería casi imposible predecir comportamientos en ciencias, ingeniería, economía y hasta en la vida diaria. Desde calcular el interés compuesto hasta predecir el clima, las funciones son herramientas vitales que nos ayudan a entender el mundo que nos rodea.
Aplicaciones Prácticas de las Funciones
En la Ciencia
Las funciones son utilizadas para modelar fenómenos naturales. Por ejemplo, en biología, las funciones pueden describir el crecimiento de poblaciones. Si conoces la tasa de natalidad y mortalidad, puedes usar funciones para predecir cuántos individuos habrá en el futuro. Esto es fundamental para la conservación y el manejo de recursos naturales.
En la Economía
En el ámbito económico, las funciones son esenciales para entender el comportamiento del mercado. La oferta y la demanda pueden representarse mediante funciones que muestran cómo cambian los precios según diferentes condiciones. Esto ayuda a los economistas a tomar decisiones informadas y a predecir tendencias económicas.
En la Tecnología
Las funciones también son fundamentales en el desarrollo de software y aplicaciones. Desde algoritmos que optimizan la búsqueda de información hasta modelos de inteligencia artificial que aprenden de los datos, las funciones son la base sobre la cual se construyen muchas tecnologías modernas. Cada vez que utilizas una aplicación, es probable que estés interactuando con múltiples funciones en segundo plano.
En resumen, las funciones son un concepto central en matemáticas y ciencias que nos permite comprender y predecir el comportamiento de diversos sistemas. Desde sus características únicas hasta sus aplicaciones prácticas, es evidente que las funciones no son solo un tema académico, sino una herramienta esencial en nuestra vida diaria. Así que la próxima vez que escuches la palabra «función», recuerda que es mucho más que una simple relación matemática; es una clave que abre la puerta a un mundo de posibilidades.
¿Qué diferencia hay entre una función y una relación?
Una función es un tipo específico de relación donde cada input tiene un único output. En cambio, una relación puede tener múltiples outputs para un mismo input.
¿Cómo puedo saber si una gráfica representa una función?
Puedes usar la prueba de la línea vertical. Si trazas una línea vertical en cualquier parte del gráfico y esta toca la gráfica en más de un punto, entonces no es una función.
¿Qué son las funciones inversas?
Las funciones inversas son aquellas que «deshacen» la acción de la función original. Si una función toma un input y lo transforma en un output, su inversa tomará ese output y lo transformará de vuelta al input original.
¿Por qué son útiles las funciones en la vida diaria?
Las funciones nos ayudan a modelar situaciones cotidianas, como calcular gastos, predecir resultados y entender patrones en datos. Nos permiten tomar decisiones informadas basadas en predicciones matemáticas.
¿Puedo crear mis propias funciones?
¡Por supuesto! Puedes crear funciones para modelar cualquier relación que observes en la vida real. Solo necesitas definir el dominio, el codominio y la regla que relaciona ambos.